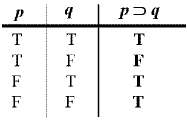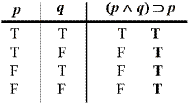A business rule is a rule that is 'of, for and by' the business community, refers to business things and is expressed in the language of the business.  An important category of business rules, typically called inference rules,^[1] involves expressions using 'if…then…', or a variant such as '….if….'.  Inference rules are also referred to as If/Then rules.  Constructions using 'if…then…' occur in other disciplines, including such technical contexts as formal modeling and programming languages, as well as in ordinary language.  This article focuses on the relationship between business rules and the if/then constructions that have been used in technical contexts to express business rules.  How well or poorly do these constructions map to business rules?  Specifically, this article addresses the following questions.

• Can if/then constructions that are used in technical contexts satisfactorily express the semantics of business inference rules?

• Can these if/then constructions be used to express business rules beyond inference rules?

The relationship between business rules and technical if/then constructions is important to the business rules approach.  Ronald Ross has claimed that business rules are based on formal logic, specifically if/then constructions as used in the predicate calculus.^[2]  The Object Management Group's (OMG) Business Semantics of Business Rules (BSBR) RFP has adopted a similar position.^[3]  This addresses a fundamental idea that grounds the business rules approach.

Although if/then statements are easily understood in both ordinary language and technical languages, they carry a myriad of meanings.  Three distinct uses of 'if…then…' are found in the following (each of which has a relationship to formal logic):^[4] 

• Truth-functional constructions
• Inferencing rules^[5]
• Rules of logic

This article describes the deep semantic issues in the relationship between business rules and these if/then constructions.  To be sure, the OMG's BSBR RFP addresses the need for a semantics of business rules.  This RFP and the activities of the OMG in this regard have been well documented in the pages of the Business Rule Journal by Stan Hendryx.  While it is certainly hoped that the BSBR standard, when it is completed, will address the issues identified here, these issues are not clearly raised in the BSBR RFP.  However, any business rules standard that claims to be based on formal logic will have to address these issues.

I. Truth-Functional Constructions

Formal logic provides constructions of the form 'if p then q' with a truth-functional meaning:

given the truth-values of its component propositions, the truth-value of the whole proposition is uniquely defined.

This concept is defined by a truth-table, which shows what value the construction has, given all the possible truth-values of its parts.  (The standard symbol for 'if…then…' in formal logic is known as the 'horseshoe':  )

The horseshoe expresses material implication.  In the sense of material implication, 'if p then q' is equivalent to 'not-p or q' (or 'not-(p and not-q)').  Each construction has the same truth-value for the same truth-value of p and q.

Material implication accommodates nesting but does not accommodate 'else'.  It is possible to have a statement of material implication involving nested uses of the horseshoe, such as

((p

q)

((r

(s

t))

u)).

However, material implication does not support a construction that can be read as 'if…then…else'.

I.A. Extending Material Implication

If/then constructions can be used in Unified Modeling Language (UML) models to state constraints on a model.  These constraints are expressed in UML by means of the Object Constraint Language (OCL)^[6].  A constraint language needs to include material implication, and OCL does this with expressions of '…implies…'.  However, 'implies' connotes a stronger sense of implication than material implication.  In OCL, 'p implies q' means that the (truth-functional) proposition 'if p then q' is true (either p is false or q is true) in every instantiation of the model to which the constraint applies.  In other words, it is conceivable that the constraint expression could be false in an instantiation of some other model, but that would have to be a model to which that constraint was not applied.

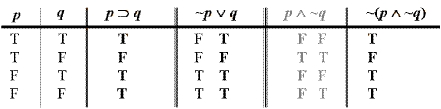
This sense of implication is subtly different from logical implication, which means that an implication is always true given any truth-value (or under every possible interpretation) of its component propositions.  In other words, there is no (logically) conceivable model in which a logical implication would be false.  Consider the expression

((p ^ q)

p),

if p and q then p.  This statement is true no matter what truth-values its constituent parts have, as shown in the following truth-table:

Logical implication is tautologous material implication.^[7]  The negation of a tautology is a self-contradictory statement (that is, a statement that is false under every possible interpretation). Logical implication would support only a trivial notion of constraints because such constraints are implicit in every model and would 'prevent' only states that are logically impossible.

I.B. Business Rules and Material Implication

Business rules are not equivalent to statements of material implication.  Very little in ordinary language is precisely equivalent to material implication.  The rub is that material implication is true when its If-part is false.  'If…then…' is often used in ordinary language to express contrary-to-fact statements.  For example, a person might say, "If I were president of the United States, my first priority would be to cure AIDS."  While a number of ordinary language responses are appropriate here, one is certainly not, "That's right because you're not the president of the United States."  In the sense of material implication, it would be true for the same reason to say, "If I were president of the United States, I would work to ensure the spread of AIDS."

Material implication is fundamental to formal logic precisely because it is neutral as to the significance of the connectivity between the If-part and Then-part.  It would be a thesis of little value to say that business rules are statements of material implication.  Yes, they are, but we are interested in what more they are.  But, clearly, we cannot go as far as to say that business rules are statements of logical implication.  Business rules are significant assertions whose violations are certainly conceivable (and are sometimes true).

I.C. Business Rules and Constraints

Many business rules seem to be closely aligned with constraints.  Indeed, we see this relationship being made in many classifications of business rules.  In Principles, Ron Ross presents the following classification of rules^[8] (see Figure 1):

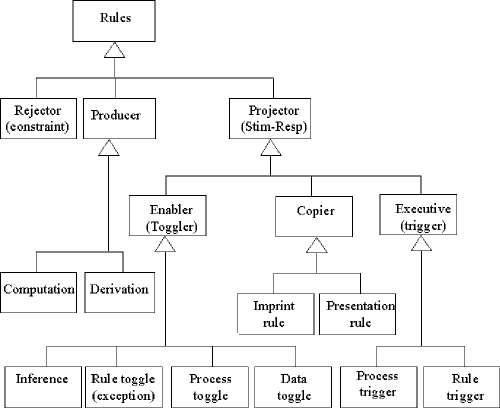
Figure 1.  Ronald Ross's Rule Classification

Rejectors are explicitly associated with constraints throughout Ross's discussion.  In a footnote, he notes that it is also possible to consider inference rules (if/then rules) to be constraints.^[9]  Here we have an assertion that a business if/then rule is a constraint.^[10]  Moreover, in the vein of considering inference rules to be constraints, Producers should also be considered constraints.

In his book Business Rules and Information Systems, Tony Morgan offers a simpler classification of business rules, but one that draws the connection between business rules and constraints even more explicitly than Ross does^[11] (see Figure 2):

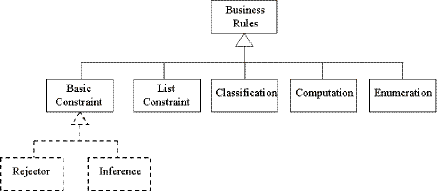
Figure 2.  Tony Morgan's Rule Classification (with Amendments)

Morgan's category of Basic Constraints can be aligned with Ross's Rejectors and inference rules.  According to Morgan, there are two formats for expressing Basic Constraints:  one involves 'must' or 'should' with an optional 'if' (or 'unless') clause; the second uses 'may…only if'.  For the purposes of this discussion, however, it will be helpful to view Morgan's Basic Constraints (as shown with the dotted boxes) in terms of Rejectors (rules expressed by a simple 'must' or 'should' statement or containing 'may…only if'^[12]), and inferences (rules containing 'must…if…').

At first, there would seem to be little loss of semantics in going from (a subclass of) business rules to OCL-style constraints.^[13]  But this is an illusion.  OCL-style constraints do not explicitly express a modality, for example, 'must (be true)'.  OCL constraints are declarative expressions whose modality^[14] is handled by the implicit semantics of the constraint itself, which states that the constraint (in the sense of invariant) is true for all possible instantiations of the model to which it applies.  Because modality is not explicit in OCL, OCL loses the ability to express the weaker modalities 'may' and 'should'.

A deeper blow to the view that OCL constraints match the semantics of business rules has been made in the proposal of the Business Rule Team (BRT) to the OMG's Business Semantics of Business Rules RFP.  The BRT argues that business rules are statements of deontic logic.^[15]  Deontic modalities are obligation, permission, and prohibition.  According to this view, a rejector of the form A must be B expresses the deontic statement that it is prohibited (forbidden) that A is not B or, equivalently, that it is obligatory (to ensure) that A is B.  Given that OCL constraints involve the alethic modality of necessity, it is not easy to see how to transform deontic statements to OCL constraints.  An intuitively acceptable axiom for converting between deontic and alethic modality is:

Modality Conversion Axiom:  Permissible-p logically implies possible-p

If it is permissible to make p true in a model, then there is at least one conceivable instantiation of that model in which p is true.  However, this axiom does not support the transformation of statements involving deontic modality to the alethically necessary statements of OCL-style constraints.  The transformation from business rules to system semantics must be supported by non-logical assumptions; for example, the system will, necessarily, fulfill the obligations specified by the business rules.

II. Inferencing Rules

Another sense of 'if…then…' is provided by rules executed by an inference engine.  This is a complex area because there are different types of inferencing rules that are executed by analogous but different inference engines.

II.A. Inferencing Rule Types and Inferencing

II.A.1. Production Rules

Production rules (PRs) are if/then rules with the structure:

IF condition
THEN (do) action

Unlike truth-functional types of if/then constructs, PRs have traditionally not accommodated nesting.

Traditionally, PRs have been supported by two types of inferencing algorithms:  forward chaining and backward chaining.  Backward chaining is goal driven; the inference engine uses rules to determine the value of an attribute (the goal).  Forward chaining is data driven; the inference engine makes inferences based on rules from given data.

The most common form of forward chaining is the Rete algorithm^[16] which, within an object-oriented (OO) context, provides a powerful form of processing sets of objects with rules.  The condition of a forward-chaining production rule under the Rete algorithm provides an SQL-like query over instances of classes; the action of the rule is performed on each 'row,' or tuple of instances, returned to the inference engine by that query.  Examples of inference engines include Computer Associates' CleverPath™ Aion® Business Rules Expert, ESI's Logist, Fair Isaac's Blaze Advisor, Haley Enterprise's Café Rete, JRules from ILog, ArtEnterprise from Mindbox and RulesPower, among others.

While some PR languages allow for if/then/else PRs, 'else' is generally dangerous to use within an inferencing context.  It means that if the inference engine happens to consider the rule and doesn't fire it, the 'else' part is executed.  It is not always clear when the inference engine will just 'consider' a rule.

In principle, the Action clause of a PR can accommodate any form of imperative code, including operation invocation, branching or even looping constructs.  As a result, PRs are highly flexible and powerful, factors that have undoubtedly contributed to the continued popularity and successful use of PRs in business rule systems.  One drawback is that PR languages tend to be highly vendor-specific, and there is no formal approach to understanding their structure or semantics.  The Rete algorithm itself is subject to different implementations.  Recently, however, there has been growing interest in standardizing the representation of PRs.^[17]

II.A.2. Logic Programming and Derivation Rules

Another use of 'if…then…' within an inferencing context is defined in logic programming (LP).  LP, as its name would indicate, is based on formal logic, specifically expressions of the predicate calculus.  The format of a rule on LP is:

head if body

where the head is an atom and the body is a set of atoms (Boolean expressions), and where universal quantification is implicit across the LP statement.  For example,

(for all x) x is a Mother if Sex of x = "Female" and x is a Parent.

LP statements are often called derivation rules.^[18]  (However, this sense of derivation rule has little to do with the business rule classification of derivation rule found in such classifications as Ross's.  Ross classifies derivation rules as a specific type of Producer (see Figure 1):  business derivation rules provide a definition of a (derived) term.  LP derivation rules, on the other hand, are more like Ross's inference rules, as will be discussed further in Section II.B.2.)  In the business rules community, Prolog, the most well-known LP language, has been used to develop business rule systems.^[19]

Inferencing with derivation rules^[20] involves a process of unification and resolution.  Expressions in the body of a rule are matched ('unified') against all the facts currently in the fact base and 'resolved' against those that render the body true.  Resolution consists of propagating the values that satisfy the variables of the expression in the body to the corresponding variables in the head.  Unification algorithms support backtracking, which is similar to depth-first (recursive) backward chaining.  Unification and resolution support backward chaining (querying whether a particular fact can be derived) as well as forward chaining (deducing facts directly from the fact base) with the same semantics -- that is, inferencing over a set of derivation rules yields the same results independently of whether inferencing is backward or forward chaining.

Like PRs, derivation rules do not accommodate nesting.  Moreover, because LP is based on expressions of the predicate calculus, 'else' is not supported within LP languages.

II.A.3. The Semantics of Inferencing Rules

The inferencing algorithm provides the semantics of 'if…then…' in the case of inferencing rules.  Thus, the if/then rule can carry the semantics of chaining (a PR) or unification and resolution (a derivation rule).  For this reason, the inferencing 'if…then…' is typically a construct of a programming language whose semantics is understood by the programmer who understands the inferencing algorithm being used.

II.A.4. The Relationship between PRs and Derivation Rules

PRs and derivation rules are conceptually different.  What is the relationship between them?  Consider the simple derivation rule:

likes(Matt, x) if likes(x, movies)

This rule adds the fact that likes(Matt, x) to the fact base for all values of x that match the fact that likes(x, movies). This rule may be transformed into the following PR in which the head becomes an explicit PR action:

If likes(x, movies)
Then AssertFact( likes(Matt, x) )

This is the 'literal' PR version of a derivation rule.  But it is not a typical PR.  In today's PR engines, PRs function in OO contexts.  Simple AssertFact actions seem out of place in this context.  PRs interact with the OO structures.  The semantics of 'likes(x, movies)' would be transformed from a fact type (atom) to an explicit query operation (of some object) that returns a Boolean.  What is queried by this operation is not specified -- it might simply be the value of an attribute or an association class.  However, the semantics of this query operation does not arise for the fact type in the derivation rule.  Also, this transformation means that the Then-part of the PR does not make sense given the semantics of 'likes'.  Does AssertFact( ) merely posit the value returned by 'likes(Matt, x)', assuming an appropriate value for x, which, in fact, would probably have no value at the point of the rule's firing?

Indeed, in the OO context of a PR, the semantics of the assertion of the object-attribute-value tuple (fact) <Order Discount 0.05> is the assignment of 0.05 to the Discount attribute of the Order object.  If 'likes(x, y)' has the semantics of a query operation, then the intended action of the PR would more likely involve the invocation of a different operation, for example, 'EstablishLikes(Matt, x)', which does something with the arguments 'Matt' and an appropriate value for x such that 'likes(Matt, x)' will return True.  However, the semantics of this method is not specified by the derivation rule.  As a general principle, atoms with the same semantics can be used in both the head and body of a derivation rule; however, using operations with the same semantics cannot be done in the condition and action of a PR.  (Semantic differences between the conditions and actions in PRs are discussed further in Section II.B.2.)

PRs allow a full range of actions to be invoked in their Then-parts.  Derivation rules, on the other hand, lack this expressivity and flexibility because they lack the ability to invoke actions. LP must be extended with additional mechanisms, called procedural attachments, which invoke action-performing procedures when facts are inferred involving specified predicates, to match the expressivity of PRs.

II.B. Inferencing Rules and Other Rules

This section examines issues regarding the relationships among inferencing rules, constraints, and business rules.  These issues are rendered more complex because inferencing rules have two different forms.

II.B.1. Inferencing Rules and Constraints

What is the relationship between constraints and PRs?  PRs involve invocations of actions, whereas constraints are Boolean expressions and thus cannot have side effects. For this reason, the attempt to render a constraint as a PR is usually unsatisfactory. A simple rendering of a constraint such as x (must be) > 0 into a PR might be:

If Not-(x > 0)
Then Stop inferencing (or some such action).

Because constraints are not productions, the precise Action clause of a PR representing a constraint is always problematic.

The treatment of constraints in terms of PRs has a curious feature.  The semantics of constraint requires that it cannot be violated in any state of system. For this rule to fire, it must be the case that the value of x has already violated the intended constraint. PRs test their conditions against the existing state. Thus, to treat constraints as PRs requires allowing the very state to exist that was prohibited by the constraint.

Moreover, the difference between inferencing rules and constraints is fundamental: constraint languages, such as OCL, do not provide an inferencing if/then construct.^[21]  The semantics of the truth-functional '…implies…' (discussed in Section I.A) does not support inferencing in the sense of inferencing rules. This statement sounds paradoxical ('implies' does not support inferencing), but it must be kept in mind that inferencing as supported by inference engines brings into play a wholly separate semantics than truth-functionality (see Section II.A.3). To be sure, inferencing provides a powerful semantics for rules, but the value of that semantics lies primarily in algorithms for processing declarative code in a special way.

It is instructive to note how languages combining LP and constraints (for example, Prolog-III) have been constructed.^[22]  Constraint atoms are introduced as a separate type of atom into an LP statement body.  These atoms cannot play a role in unification but must be checked at the end of the resolution step to determine the validity of adding the new, resolved fact to the fact base and constraint network.  An LP language supporting constraints must have two engines:  an inference engine and a constraint engine.  The latter acts upon the request of the inference engine to ensure that constraints are not violated.  Even where derivation rules and constraints have been integrated into one language, their respective semantics requires that they be processed under different regimes.

A consequence of this is that the business rule classification of inference rules as constraints confronts a dilemma.  If inference rules are really used in inferencing in the sense defined for inferencing rules, then they are not constraints in the technical sense of OCL, and if they are OCL-style constraints, they cannot support inferencing.  What Ross envisions as inferencing seems to be very close to inferencing with derivation rules^[23], but combining constraints and derivations is not simply a matter of treating inferencing rules as constraints.  Resolving this dilemma by providing a clear business meaning of both 'inference rule' and 'constraint' is a challenge for the formulators of the OMG's BSBR standard.

II.B.2. Inferencing Rules and Business Rules

In general, both PRs and derivation rules can map to only a subset of business rules.  (In this context, mapping to business rules means the technical expression without significant semantic loss or transformation.)  This relationship is illustrated in Figure 3.  Because both PRs and derivation rules are constructs in a programming language, it is assumed that they will be used for other purposes than simply for implementing business rules.  In Figure 3, these other rules are called 'System Rules' -- they do the 'system things' programs also have to do but which must be kept separate from the business rules.

Figure 3.  Business Rules and Inferencing Rules

The subset of business rules to which inferencing rules map might vary.  Both derivation rules and PRs can map to Ross's inference rules and Producers.  Because PRs support action invocations, PRs can also map to (some) Projectors as well.  (With the addition of procedural attachments, derivation rules might support Projectors as well.)  On the other hand, PRs cannot represent Ross's Rejectors; however, an LP language with constraints might map to some Rejectors as well (if the issue over the deontic modality of rejectors is ignored).

On the surface, however, inference rules seem to have more affinities with derivation rules than with PRs.  The format of derivation rules, <head> if <body>, matches the 'conclusion if condition' format preferred by the Business Rules Approach (BRA) for inference rules^[24] more closely than does the 'if condition then action' format of PRs. Indeed, according to the BRA, rules should not have multiple conclusions. Inference rules, thus, closely resemble a common subtype of derivation rule known as a Horn expression. And both inference rules and derivation rules do not support 'else'.

Moreover, PRs have the disadvantage of requiring a greater 'semantic' shift in going from the business rules to the PR than do derivation rules.  The semantic shift occurs in the Then-part of the rule.  We can illustrate the semantic shift with the following example.  Consider an inference rule (that is, a business rule) of the form:

C is D if A is B

In the business rule, there should be no ambiguity in the 'is', which can be expressed with the equals of equality ('= =').

C = = D if A = = B

On the other hand, the typical PR implicitly involves a shift to the equals of assignment in the Then-part:

If A = = B		// equals of equality, a condition
Then C = D		// equals of assignment, an action

There appears to be less of a semantic shift in going from business rules to derivation rules because the same semantics (equality) is used across both the head and body of a derivation rule.  That is an advantage of using the same type of atoms in both the head and body.  PR languages hide this shift because it is an inherent part of semantics of the Then-clause of PRs.

One issue remains:  What is the role of inferencing in business rules?  It is unclear whether, in stipulating that formal logic is the basis of the business semantics of business rules, the OMG's BSBR RFP intends to imply that rules of logical inference provide the logical forms of reasoning for business rules.  Inferencing of the type involved with inferencing rules (see Section II.A) is not the inferencing strategy supported in formal logic.  Inferencing in formal logic is based on the Rules of Logic, which are discussed next in Section III.

III. Rules of Logic

Formal logic also provides formal rules of logical inference.  For example, modus ponens says,

"If given p and a statement that if p then q, then we may infer q."

At a minimum, formal logic provides rules of the proposition calculus.  Rules of logic might also include the rules of traditional syllogistic logic (for example, if all Greeks are human, and all humans are mortal, then all Greeks are mortal) as well as the rules of first order logic (FOL), or the predicate calculus (for example, instantiation and generalization of quantified expressions), which, in the opinion of many, have superseded syllogistic logic.  Also, formal logic encompasses a myriad of extensions beyond FOL for various modal logics and other special logics (for example, higher order logics that allow quantification over predicates).

Rules of logic are 'meta' rules about statements that occur in a system.  Like inferencing rules, rules of logic admit neither nesting nor 'else'.  However, unlike inferencing rules, every logical rule of inference corresponds to a logical implication of formal logic.  For example, modus ponens corresponds to the logical implication

((p ^ (p

q))

q).

Forward chaining is analogous to modus ponens, but whereas forward chaining usually suffices for the needs of production rule inferencing, modus ponens by itself cannot constitute a complete system of the rules of logic.  Moreover, forward chaining is an algorithm executed by a computer; rules of logic are formal statements about the possible, valid manipulation of statements in a system.

Although LP is also based on FOL, the relationship between LP and FOL is by no means straightforward. Critical differences occur in the following areas:^[25]

• Expressiveness.  Logic programs supporting negation as failure treat not-p as meaning p is untrue, that is, either p is false or p is unknown.  Classical negation, which is supported in FOL, treats not-p as meaning p is false.  Classical negation implies negation as failure, but not vice versa.  On the other hand, FOL can support some things that logic programs cannot express, such as positive disjunctions.

• Support for actions.  Neither LP nor FOL natively provides a means to express actions; however, LP can accommodate actions through an extension (procedural attachments).  It is not even theoretically understood how to incorporate actions into FOL.

• Structure of inferencing.  Support for negation as failure leads a sophisticated form of inferencing in LP, called nonmonotonic inferencing, in which facts inferred at one point might be rendered invalid with the addition of further facts drawn on the basis of further inferences.  FOL, because it supports only classical negation, supports only monotonic inferencing.  The requirements for inferencing within business rules have never been sufficiently defined to specify which form of inferencing is appropriate.

The semantics for business rules needs to address the relationship between LP and FOL approaches with respect to formal logic, especially as it concerns inferencing.  I would urge that only the rules of logic satisfy the requirements of the Computation Independent Model (CIM) of the OMG's Model Driven Architecture (MDA), which is the target modeling perspective of the BSBR RFP.  (For a description of the MDA, see the sidebar, "An Overview of the Model Driven Architecture.")  Other forms of inferencing, as defined for inferencing rules, are specific algorithms, and therefore inherently computational.  However, the rules of logic are, in general, not well understood within the programming and system engineering communities.^[26]

IV. Conclusions

This article only scratches the surface in comparing business rules with the semantics of the technical expressions that allegedly express business rules.  A complete discussion would need to encompass conditionality ('if…then…', as this article covers), constraints, and events.  For example, in this article, the meaning of constraint is restricted to its meaning in OCL as an invariant.  But the meaning of constraint varies as widely as that of 'if…then…' but with much less discipline.  Thus, more might said on the complex subject of constraints and business rules.  The relationship between business rules and events -- a topic that includes the relationship between business rules and Event-Condition-Action (ECA) rules -- must also be addressed. 

This article attempts to explain the semantics of business rules, especially inference rules, on the basis of the more precisely defined semantics of different types of if/then constructions in formal logic.  This exploration has raised more issues than it has apparently resolved:

• Mapping the modalities of business rules to the semantics of system analysis and computer programs.  This issue is especially critical if business rules are deontic statements.  See Section I.C.
• Clarifying the relationship of constraints and inference rules at the business level, especially if inference rules are considered to be constraints but yet support inferencing.  See Section II.B.1.
• Resolving the relationship between rules of logic and LP.  Resolving this issue will define what kind of inferencing is involved in business rules.  See Sections II.B.2 and III.

Hopefully, resolutions of these issues will come with the OMG's BSBR standard.  In the meantime, these issues must be recognized.  Worse than the subtle differences in rule semantics and the complex rule relationships those differences create is the muddling and blurring of rule semantics and those relationships with simplifications.  However, resolving these issues can come only by way of an industry effort and agreement as currently underway within the OMG.

---

I want to thank Gerd Wagner of the University of Eindhoven, and one of the founders of the RuleML Initiative, for his comments on this article.  Helpful advice was also provided by Leo Hermans.

References

[1]  Ronald G. Ross, Principles of the Business Rule Approach, Addison-Wesley (2003).  

[2]  Ross, Principles, p. 231.  

[3]  Business Semantics of Business Rules RFP, URL: www.omg.org/cgi-bin/doc?br/03-06-03: "The BRM shall capture Business rules in a way that is consistent with formal logics…" (para 6.5.2.3).  

[4]  A fourth type of if/then construction, branching over a set of instructions, is probably the most familiar to computer programmers.  This sense of "if…then…" accommodates both nesting and the use of "else."  However, because it is not related to formal logic and because it is a procedural construct, branching has little affinity to business rules and is not considered further in this article.  

[5]  In this article, the business rule classification "inference rule" refers to if/then business rules, and "inferencing rule" refers to if/then rules that are executed in an inferencing context.  Inferencing rules, and their relation to inference rules, are discussed in Section II of this article.  

[6]  Jos Warmer and Anneke Kleppe, The Object Constraint Language, Addison-Wesley (1999).  

[7]  Peter Suber, "Glossary of First-Order Logic," URL: http://www.earlham.edu/~peters/courses/logsys/glossary.htm  

[8]  Ross, Principles, pp. 142–143  

[9]  Ross, Principles, p. 142.  Ross discusses this point further in Principles, pp. 247–251.  

[10]  This point was discussed by the author in "Business Rules, Platforms, and Inferencing," in the Business Rules Journal, Vol. 4, No. 10 (October 2003), URL: http://www.BRCommunity.com/a2003/b169.html.  This theme also occurs in Tony Morgan's business rule classification scheme.  

[11]  Tony Morgan, Business Rules and Information Systems, Addison-Wesley (2002), Section 3.2.2, Rule patterns, pp. 69–71.  

[12]  Ross, Principles, pp. 145-147.  

[13]  In this article, the word constraint is used in the sense of a UML invariant.  

[14]  The modality involved here is called alethic modality:  pertaining to the mode of truth of a statement, p.  Alethic modalities are necessity (N), possibility (P), and contingency (C) where:  Np = ~P~p; Cp = P~p.  

[15]  Available at http://www.omg.org/cgi-bin/doc?br/2003-06-03, as presented at the OMG Technical Conference, Anaheim, CA, February 2, 2004, available at http://www.omg.org/cgi-bin/doc?bei/2004-01-04.  For a summary by one of its authors, see John Hall, "Business Semantics of Business Rules," Business Rules Journal, Vol. 5, No. 3 (March 2004), URL: http://www.BRCommunity.com/a2004/b182.html.  

[16]  Charles L. Forgy, "Rete:  A fast Algorithm for the Many Pattern/Many Objects Pattern Match Problem," Artificial Intelligence, 19 (1982), pp. 17-37.  See also http://www.ai.mit.edu/courses/6.034b/recitation6.pdf  Development of the Rete algorithm has led to the Rete II algorithm, which supports recursive forward-chaining rules (RFCs).  RFCs provide a means of nesting forward-chaining rules.  The value of RFCs for representing business rules, however, is dubious, because nested rules violate the atomicity of business rules.  As is the general case with PRs, RFCs are clearly programming constructs  

[17]  See the OMG's Production Rule Representation RFP at http://www.omg.org/cgi-bin/doc?br/03-09-03.  The RuleML Initative, http://www.ruleml.org, also intends to address the representation of production rules.  

[18]  This terminology is found in the RuleML Initiative.  See Gerd Wagner, et. al., "MOF-RuleML:  The Abstract Syntax of RuleML as a MOF Model," URL: http://www.omg.org/cgi-bin/doc?br/03-10-01  

[19]  Markus Schacher, "Business Rules in Prolog," Business Rules Journal, Vol. 3, No. 10 (October 2002), URL: http://www.BRCommunity.com/a2002/b118.html  

[20]  For a discussion, see Benjamin N. Grosof, et. al., "Description Logic Programs:  Combining Logic Programs with Description Logic," URL: http://ebusiness.mit.edu/bgrosof/ section 7.  

[21]  "Eindhoven University of Technology response to the Business Rules in Models RFI," section 7.1, URL: http://www.omg.org/cgi-bin/doc?ad/03-01-24  

[22]  For a discussion, see Brian Mayoh, et. al., "Constraint Satisfaction and Constraint Programming:  A Brief Lead-in," Constraint Programming, ed. Brian Mayoh, et. al. Springer-Verlag (1994), pp. 10-11.  For more information on PROLOG III, visit http://portal.acm.org/citation.cfm?id=79210&dl=ACM&coll=portal/.  

[23]  Compare Section II.B.2 of this paper with Ross's discussion of backward and forward chaining in Principles, pp. 250—251.  Primary similarities are the implication that the Then-part of an inference rule is inferred to be true by the inference engine (pp. 247—248) and the neutrality between backward and forward chaining to the rules themselves.  

[24]  Ross, Principles, pp. 150—151 and Appendix D; also Morgan, Business Rules and Information Systems, p. 69.  

[25]  The following discussion is drawn from Grosof, et. al., "Description Logic Programs," Section 2.  

[26]  This point is also made by Benjamin N. Grosof, et. al., "Description Logic Programs."  For example, consider the complications of existential instantiation.  '(x)(Px)' cannot be instantiated to 'Pa' because there is no reason to assume that an arbitrarily selected individual, a, is a P; nor can it be instantiated to 'Px' because it would be indistinguishable from universal instantiation.  

# # #