Verbalizing Business Rules (Part 8)
Business rules should be validated by business domain experts, and hence specified using concepts and languages easily understood by business people. This is the eighth in a series of articles on expressing business rules formally in a high-level, textual language. This article discusses verbalization of equality constraints.
The first article[4] discussed criteria for a business rules language, and verbalization of simple uniqueness and mandatory constraints on binary associations. The second article[5] examined hyphen-binding, and verbalization of internal uniqueness constraints that span a whole association, or that apply to n-ary associations. The third article[6] covered verbalization of basic external uniqueness constraints. The fourth article[7] considered relational-style verbalization of external uniqueness constraints involving nesting or long join paths, as well as attribute-style verbalization of uniqueness constraints and simple mandatory constraints. The fifth article[8] discussed verbalization of mandatory constraints on roles of n-ary associations, and disjunctive mandatory constraints (also known as inclusive-or constraints) over sets of roles. The sixth article[9] considered verbalization of value constraints. The seventh article[10] examined verbalization of subset constraints.
Verbalization of equality constraints between single roles
Figure 1 shows a fragment from an ORM schema about hospital
patients discussed in [11]. The circled '=' connecting the roles played by Patient indicates that for each state of the
business domain, the population of these two roles must be equal. In other
words, if we know a patient's systolic BP (blood pressure), we also know his/her
diastolic BP, and vice versa. This illustrates a simple equality constraint
between two fact type roles.
An equality constraint may be applied only if the roles are compatible (i.e., based on identical or overlapping types). At the external level, BP is usually displayed as a single figure, for example 120/80, read as "120 over 80", where the first number measures the systolic blood pressure (maximum pressure exerted when the heart contracts) in millimeters of mercury, and the second number indicates the diastolic blood pressure (pressure in the arteries when the heart is at rest). In this schema, the two facts underlying the overall BP reading are displayed separately.
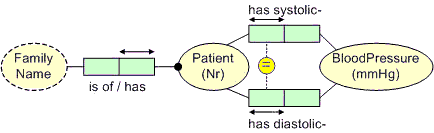
Figure 1. An equality constraint between single roles.
This equality constraint may be formally verbalized in any of the following ways:
Each Patient who has a
systolic BloodPressure also has a diastolic BloodPressure and conversely. |
|||
For each Patient: |
|||
that Patient has a systolic BloodPressure
if and only if that Patient has a diastolic BloodPressure. |
|||
For each Patient1: |
|||
Patient1 has a systolic BloodPressure
if and only if Patient1 has a diastolic BloodPressure. |
|||
If a Patient has a systolic BloodPressure
then that Patient has a diastolic BloodPressure and conversely. |
|||
If a Patient has a systolic BloodPressure
then that Patient has a diastolic BloodPressure and |
|||
if a Patient has a diastolic BloodPressure
then that Patient has a systolic BloodPressure. |
|||
The last two readings reflect the fact that an equality constraint between two
arguments is equivalent to a conjunction of two subset constraints, one in either
direction. As usual, the pronoun 'who'
may be replaced by 'that' or 'which', the quantifier 'a' may be replaced by 'some',
'at least one', or 'an', 'for
each' may be replaced by 'given
any', and 'if and only if'
may be abbreviated to 'iff'.
As explained in an earlier article[5], the use of
hyphens in the predicates binds the adjectives 'systolic' and 'diastolic' to the
object type name, so the quantifier 'a'
precedes them in the verbalization.
Figure 2 shows a UML class diagram for our patient example, assuming that the
blood pressure facts are modeled in terms of attributes rather than associations.
As there is no graphic way of depicting the equality constraint in UML, it is expressed
in OCL within an attached note. Because the note is attached to the Patient class, this is understood to provide
the context for the OCL constraint. Clearly, each of the verbalization patterns
shown above provides a higher-level declaration of the constraint that is more likely
to be understood by a non-technical domain expert.
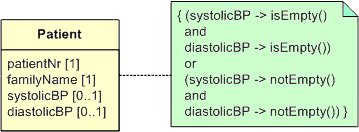
Figure 2. The ORM schema from Figure 1 expressed as a UML class diagram.
In addition to the relational-style verbalization already discussed, an attribute-style verbalization may be provided, as follows. Although less natural than the relational-style verbalization, it is likely to be more understandable to non-technical people than the OCL formulation.
For each Patient: |
|||
systolicBP exists if and only if diastolicBP
exists. |
|||
Note that this verbalization may also be applied directly to the ORM schema, so long as we supply the attribute names used in the UML diagram as corresponding role names on the ORM schema.
Though rare in practice, an n-ary version of an equality constraint may
be applied to a set of three or more compatible roles (or role-sequences).
This is equivalent to multiple binary equality constraints between all the pairs
of roles (or role-sequences). A simple example is shown in Figure 3, in both
ORM and UML notations. The '{U1}'
annotation is a non-standard extension to UML to express the uniqueness constraint
that each star name refers to at most one star[6].
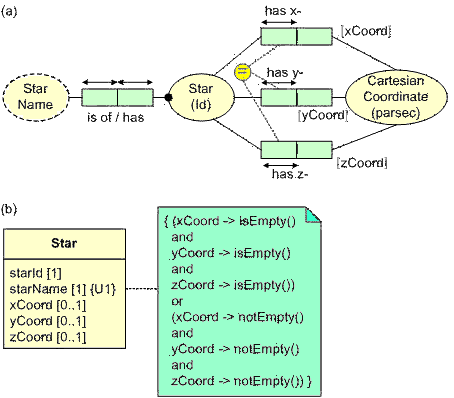
Figure 3. An n-ary equality constraint in (a) ORM, and (b) UML.
Such n-ary constraints may be verbalized either as conjunctions of n-1
binary constraints, or directly as follows in relational-style or attribute-style.
(The latter verbalization applies also to the ORM schema, using the role names supplied
there.) If desired, a synonym for 'not
exists' such as 'is absent'
may be introduced. Note that there is no simple extension based on 'iff'; for example, p
iff (q and r) is true in some cases other than the cases where
p, q,
and r are either all true
or all false.
For each Star all or none of the following
are true: |
|||
that Star has an x-CartesianCoordinate; |
|||
that Star has a y-CartesianCoordinate; |
|||
that Star has a z-CartesianCoordinate. |
|||
For each Star: |
|||
(xCoord exists and yCoord exists and
zCoord exists) or |
|||
(xCoord not exists and yCoord not
exists and zCoord not exists). |
|||
Verbalization of equality constraints between role sequences
Equality constraints may also be specified between compatible role sequences
(of two or more roles). Consider a hospital domain where patients may have
their blood pressure measured at most once a day, and where a history is kept of
the results. Figure 4 shows one way to model this in ORM. Here the equality
constraint is between the Patient-Date
role-pairs projected from the two ternary associations. The constraint indicates
that for any given patient and date, we know either both the systolic and diastolic
BP readings, or neither reading.
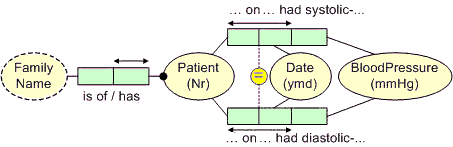
Figure 4. An equality constraint between role-pairs.
This pair-equality constraint may be verbalized in relational style as follows.
Each Patient who on a Date
had a systolic BloodPressure also on that Date had a
diastolic BloodPressure |
|||
and conversely. |
|||
For each Patient and Date: |
|||
that Patient on that Date had
a systolic BloodPressure |
|||
if and only if |
|||
that Patient on that Date had
a diastolic BloodPressure. |
|||
For each Patient1 and
Date1: |
|||
Patient1 on Date1 had
a systolic BloodPressure |
|||
if and only if |
|||
Patient1 on Date1 had
a diastolic BloodPressure. |
|||
If a Patient on a Date had a
systolic BloodPressure then that Patient on that Date had a
diastolic BloodPressure |
|||
and conversely. |
|||
If a Patient on a Date had a
systolic BloodPressure then that Patient on that Date had a
diastolic BloodPressure and |
|||
if a Patient on a Date had a
diastolic BloodPressure then that Patient on that Date had a
systolic BloodPressure. |
|||
As discussed in earlier articles, if the same object type plays more than one role in an association, either role names, or numeric subscripts appended to the object type name, may be used to distinguish the role players.
In UML it would be unusual to model this example using ternary
associations. Instead one would normally introduce a BPtest
class, as shown in Figure 5 (an identifier for BPtest
is assumed). This removes the need to verbalize a role-sequence equality constraint
in this case. Note that this modeling alternative would normally be preferred
in ORM as well, where an explicit identifier such as TestNr
would be also included to identify blood pressure tests. For a discussion of
optimization heuristics for ORM schema transformation, see chapter 12 of [1].
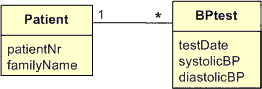
Figure 5. Remodeling in UML of the Figure 4 domain avoids the need for an equality constraint.
These verbalization patterns may be extended in obvious ways to cater for other cases, where the role-sequences may contain more than two roles, or are projected from a role path spanning multiple associations. As a simple example of the former, consider the equality constraint in Figure 6. Here each role sequence contains three roles projected from one of the ternaries. In this domain, patients may have their blood pressure measured at any given clinic at most once a day, but may attend multiple clinics on the same day. A history is kept of the results.
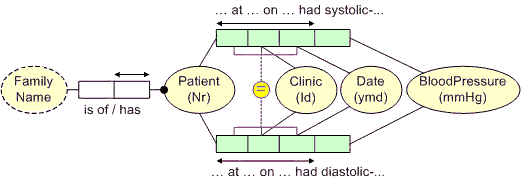
Figure 6. An equality constraint between two role-sequences, each of which contains 3 roles.
This equality constraint may be verbalized by simply generalizing the previous patterns. For example:
For each Patient, Clinic and Date: |
||
that Patient at that Clinic on
that Date had a systolic BloodPressure |
||
if and only if |
||
that Patient at that Clinic on
that Date had a diastolic BloodPressure. |
||
As a simple example of a subset constraint involving a projection
from a role path, consider the ORM schema shown in Figure 7. The equality
constraint declares that a person lives in a country if and only if that person lives
in a state that is in that country. Here one role pair comprises the predicate
within the fact type Person lives in Country.
The other role pair is obtained by projecting on the first and last roles of the
join path Person lives in a State that is in
Country. This path involves a conceptual join between
the roles on that path that are played by State.
For further discussion of such join-constraints, see [2].
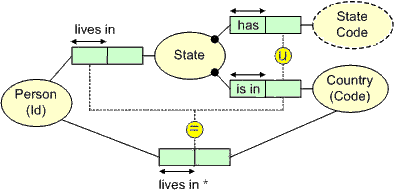
Figure 7. An equality constraint involving a role path projection.
The asterisk on the Person lives in Country
association indicates that this fact type is derived. In this case, the derivation
rule is captured by the equality constraint, and may be verbalized thus:
Person lives in Country iff |
||
Person lives in a State that is
in that Country. |
||
If this rule is added as a textual derivation rule to the ORM diagram, the graphical
equality constraint would normally be omitted. Note that the left-hand expression
in the rule denotes a simple fact type, while the right-hand side of this verbalization
applies the existential quantifier ('a')
to the join object type (State)
on the role path. The equality constraint is suitable for deriving the left-hand
fact type but cannot be used to derive the state in which a person lives. The
high-level verbalization of the rule may be formally captured by the following logical
expression:
x:Person
y:Country [x lives in y
z:State (x lives in z & z is in y)]
If one argument of an equality constraint comprises all the roles in a fact type
F, and the other argument
is a role projection from a path containing more roles, then the equality constraint
provides a full derivation rule (iff
rule) for the fact type F. Similarly, a
subset constraint from a role projection to a fact type provides a partial derivation
rule (if rule) for that fact
type. For example, if we can know that some people live in some country without
knowing the state they live in (our knowledge is incomplete), then the equality constraint
is replaced by a subset constraint, and the fact type Person
lives in Country is only partially derivable from the join path.
Full (but not partial) derivation rules for a fact type
may be captured in UML by annotating the derived association with a slash '/' and adding the derivation rule in text. In Figure
8 this rule is specified in OCL[13].
This attribute version of the rule may also be used in ORM if desired. As UML
lacks any graphical notation for specifying value-based identification schemes, I've
indicated the simple identification schemes using '{P}'
and the composite identification scheme with a note. I'll say more about derivation
rules in a later article.
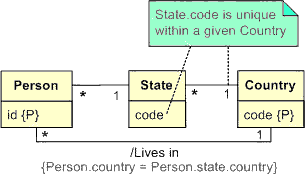
Figure 8. Specifying a derivation rule in UML.
That completes our coverage of equality constraints and their verbalization. The next article considers exclusion constraints.
References
[1] T.A. Halpin. Information Modeling and Relational
Databases. Morgan Kaufmann, San Francisco, 2001. ![]()
[2] T.A. Halpin. "Join Constraints," Proc.
EMMSAD'02: 7th Int. IFIP WG8.1 Workshop on Evaluation of Modeling Methods in Systems
Analysis and Design. Toronto, (June, 2002). Available online at http://www.orm.net/pdf/JoinConstraints.pdf ![]()
[3] T.A. Halpin. "Metaschemas for ER, ORM and UML Data Models: A Comparison," Journal of Database Management, Vol. 13, No. 2 (2002), pp. 20-29. Idea Publishing Group, Hershey, PA, USA.
[4] T.A. Halpin. "Verbalizing Business Rules
(part 1)," Business Rules Journal, Vol. 4, No. 4 (April 2003).
URL: http://www.BRCommunity.com/a2003/b138.html ![]()
[5] T.A. Halpin. "Verbalizing Business Rules
(part 2)," Business Rules Journal, Vol. 4, No. 6 (June 2003). URL: http://www.BRCommunity.com/a2003/b152.html ![]()
[6] T.A. Halpin. "Verbalizing Business Rules
(part 3)," Business Rules Journal, Vol. 4, No. 8 (August 2003).
URL: http://www.BRCommunity.com/a2003/b163.html ![]()
[7] T.A. Halpin. "Verbalizing Business Rules
(part 4)," Business Rules Journal, Vol. 4, No. 10 (October 2003).
URL: http://www.BRCommunity.com/a2003/b172.html ![]()
[8] T.A. Halpin. "Verbalizing Business Rules
(part 5)," Business Rules Journal, Vol. 5, No. 2 (February 2004).
URL: http://www.BRCommunity.com/a2003/b179.html ![]()
[9] T.A. Halpin. "Verbalizing Business Rules
(part 6)," Business Rules Journal, Vol. 5, No. 4 (April 2004).
URL: http://www.BRCommunity.com/a2003/b183.html ![]()
[10] T.A. Halpin. "Verbalizing Business Rules
(part 7)," Business Rules Journal, Vol. 5, No. 7 (July 2004). URL: http://www.BRCommunity.com/a2003/b198.html ![]()
[11] T.A. Halpin, K. Evans, P. Hallock, & B. MacLean.
Database Modeling with Microsoft Visio for Enterprise Architects. Morgan
Kaufmann, San Francisco, 2003. ![]()
[12] Object Management Group. UML 2.0 Infrastructure. Object Management Group, 2003. URL: http://www.omg.org/uml
[13] Object Management Group. UML 2.0 Object
Constraint Language. Object Management Group, 2003. URL: http://www.omg.org/uml ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules