This is the fourteenth article in a series on logic-based approaches to data modeling. The first article [5] briefly overviewed deductive databases, showing how simple data models with asserted and derived facts may be declared and queried in LogiQL [2, 22, 24], a leading edge deductive database language based on extended datalog [1]. The second article [6] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types. The third article [7] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them. The fourth article [8] discussed external uniqueness constraints. The fifth article [9] covered derivation rules in some more detail, and inclusive-or constraints. The sixth article [10] discussed simple set-comparison constraints (i.e., subset, exclusion, and equality constraints), and exclusive-or constraints. The seventh article [11] covered subset constraints between compound role sequences, including cases involving join paths.

The eighth article [12] discussed exclusion and equality constraints between compound role sequences. The ninth article [13] explained how to declare basic subtyping. The tenth article [14] discussed how to declare relationships to be irreflexive (using a ring constraint) and/or symmetric (using a ring constraint or a derivation rule). The eleventh article [15] showed how to constrain a relationship to be asymmetric and/or intransitive. The twelfth article [16] discussed recursive derivation rules, and how to constrain ring relationships to be acyclic and/or strongly intransitive. The thirteenth article [17] showed how to declare internal and external frequency constraints.

The current article discusses how to declare object and role cardinality constraints, as well as value-comparison constraints. The LogiQL code examples are implemented using the free cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL, accessible at https://developer.logicblox.com/playground/.

Object Cardinality Constraints and Role Cardinality Constraints

In mathematics, the cardinality of a set is the number of (distinct) elements that belong to the set. For example, using "#" for the cardinality function and braces "{", "}" for set delimiters, #{2, 4, 6} = 3 and #{ } = 0. Object-Role Modeling (ORM) [18, 19, 20] uses the term "cardinality" in the same sense, where the set is either a population of an object type or a population of a fact role. This is very different from what the term "cardinality constraint" means in Entity Relationship (ER) modeling [3], or what the term "multiplicity constraint" means in the Unified Modeling Language (UML) [24]. As neither ER nor UML support a graphical notation for object and role cardinality constraints we shall ignore them for the rest of this section.

Figure 1(a) shows a populated ORM model that records the name of the current president of the United States. The object type US_President is depicted as a named, soft rectangle, with its reference mode ".Name" shown in parenthesis, indicating that US presidents are primarily identified by their name. The "# ≤ 1" notation next to the object type shape depicts an object cardinality constraint to ensure that the cardinality (number of members) of the population of US_President is less than or equal to one (i.e., 0 or 1) for each state of the database. The NORMA tool [4] for ORM verbalizes this constraint as "Each population of US_President contains at most 1 instances."

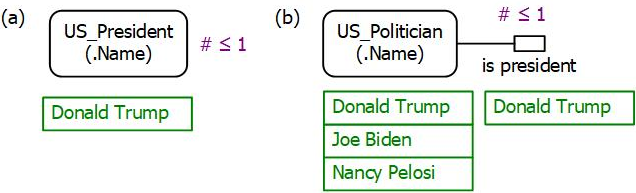
Figure 1. An ORM model with (a) an object cardinality constraint, and (b) a role cardinality constraint.

Figure 1(b) shows a populated ORM model that records the names of some current politicians of the United States, using a unary fact type "US_Politician is president" to indicate who is the president. Here the "# ≤ 1" notation next to the single role shape in this fact type depicts a role cardinality constraint to ensure that the cardinality of the population of this presidential role is at most one for each state of the database. The NORMA tool for ORM verbalizes this constraint as "For each population of "US_Politician is president", the number of US_Politician instances is at most 1."

The ORM schema in Figure 1(a) may be coded in LogiQL as shown below. The first line of code declares the entity type US_President, and types its refmode predicate which injectively maps instances of US_President to president name instances stored as character strings. The right-arrow "->" is read as "implies". A derivation rule then uses the aggregate count function to derive the number of US presidents. The left-arrow "<-" is read as "if". If no US presidents are currently recorded, you might expect this count function to return 0. However, the LogiQL count function returns no value at all if it doesn't find any facts satisfying the condition. To ensure that 0 is returned for such empty set cases, we assign 0 as the default value for the count function. This is coded as shown, using the lang:defaultValue metapredicate followed by square brackets that enclose the grave accent character "`" followed by function name. Finally, the object cardinality constraint is declared.

US_President(p), hasUS_PresidentName(p:pn) -> string(pn).
// The number of US presidents is the count of all the facts where something is a US president
nrUS_Presidents[] = n <-
agg<<n = count()>>US_President(_).
// The default value of the nrUS_Presidents function is 0.
lang:defaultValue[`nrUS_Presidents] = 0.
// For each state of the database, there is at most one US president
nrUS_Presidents[] = n -> n <= 1.

To enter the schema in the free, cloud-based REPL tool, use a supported browser to access the website https://repl.logicblox.com. The latest version of the REPL tool appears to require you to explicitly create a workspace before adding code blocks to it. To do this, simply enter the following code, and wait for confirmation that the workspace is created:

create --unique

Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block. After the "/>" prompt, type the letter "a", and click the addblock option that then appears. This causes the addblock command (followed by a space) to be added to the code window. Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code.

Now copy the full schema code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 2). By default, the REPL tool also appends an automatically generated identifier for the code block. Alternatively, you can enter each line of code directly, using a separate addblock command for each line.

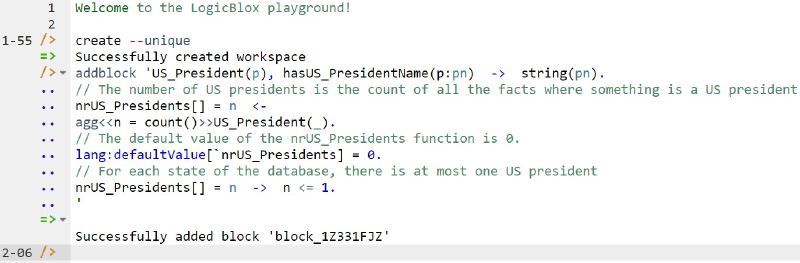
Figure 2. Creating a workspace and then adding a block of schema code.

The data in Figure 1(a) may be entered in LogiQL using the following delta rule. A delta rule of the form +fact inserts that fact. Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes. Hence, it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.

+US_President(p1), +hasUS_PresidentName(p1:"Donald Trump").

Delta rules to add or modify data are entered using the exec (for 'execute') command. To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list. A space character is automatically appended. Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules. Now copy the lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. A new prompt awaits your next command (see Figure 3).

Figure 3. Adding the data.

Now that the data model is stored, you can use the print command to inspect the contents of any predicate. For example, to list the names of the US presidents, type "p" then select print from the drop-down list, then type a space followed by "U", then select US_President from the drop-down list and press Enter. Because US_President is an entity type, an internal id is returned as well as the president's name. Similarly, you can use "n" to select and print the value of the nrUS_Presidents function.

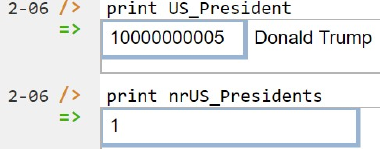
Figure 4. Printing the entries for US_President and nrUS_Presidents.

To check that the object cardinality constraint is actually enforced, try to execute the following delta rule, to assert a second US president for the same database state:

+US_President(p2), +hasUS_PresidentName(p2:"Joe Biden").

This attempted update generates an error message as it violates the object cardinality constraint by asserting that the number of US presidents is 2. Figure 5 displays part of the error message.

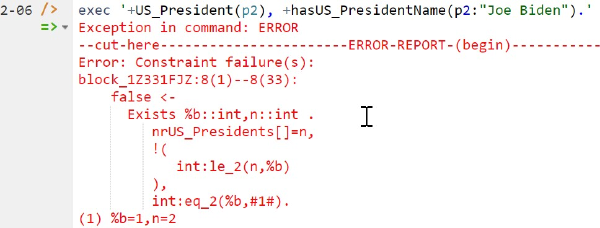
Figure 5. An error message is generated if an attempted update violates a constraint.

The ORM schema in Figure 1(b) may be coded in a similar way, as shown below.

US_Politician(p), hasUS_PoliticianName(p:pn) -> string(pn).
isPresident(p) -> US_Politician(p).
// The number of US presidents is the count of all the facts where a US politician is president
nrUS_Presidents[] = n <-
agg<<n = count()>>isPresident(_).
// The default value of the nrUS_Presidents function is 0.
lang:defaultValue[`nrUS_Presidents] = 0.
// For each state of the database, there is at most one US president
nrUS_Presidents[] = n -> n <= 1.

The data in Figure 1(b) may be entered in LogiQL using the following delta rules.

+US_Politician(p1), +hasUS_PoliticianName(p1:"Donald Trump"), +isPresident(p1).
+US_Politician(p2), +hasUS_PoliticianName(p2:"Joe Biden").
+US_Politician(p3), +hasUS_PoliticianName(p3:"Nancy Pelosi").

To perform a query, you specify a derivation rule to compute the facts requested by the query. For example, if you enter the above schema and data for Figure 1(b), the following query may be used to list the name of each recorded US politician who is not the president. The rule's head uses an anonymous predicate to capture the result derived from the rule's body. The head variable pn is implicitly universally quantified. The variable p introduced in the body is implicitly existentially quantified. A comma "," denotes the logical conjunction operator (and), and an exclamation mark "!" denotes the logical negation operator (not).

_(pn) <- hasUS_PoliticianName(p:pn), !isPresident(p).

In LogiQL, queries are executed by appending their code in single quotes to the query command. To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter. Figure 6. displays a screenshot after entering the schema and data and issuing the sample query. For the small population entered, the query returns just two US politicians who are not the president.

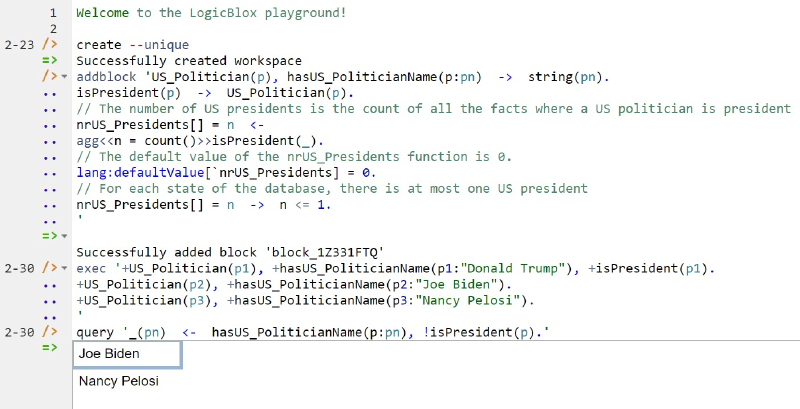
Figure 6. Adding the model and a query to list the name of each recorded US politician who is not the president.

Although useful, object and role cardinality constraints tend to be declared only rarely in ORM, as they are often implied by other existing value constraints or frequency constraints. For example, an {'M', 'F'} value constraint on Gender(.Code) implies the object cardinality constraint "# ≤ 2" on Gender. For further examples, see p. 289 of [20].

Value-Comparison Constraints

Table1. Some details about famous scientists.

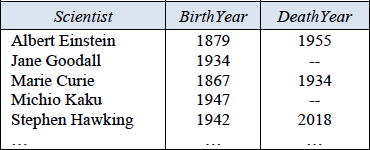
Table 1 lists the names of some famous scientists, as well as their birth year. Those who are not currently alive also have their death year recorded. Here, scientists are identified simply by their name, and years are identified by their CE (Common Era) year number. A double hyphen "--" is used to indicate that the scientist has not yet died.

Figure 7(a) shows an ORM schema for this example, as well fact tables populating the fact types "Scientist was born on Date" and "Scientist died on Date" with the sample data. Names of the roles hosted by Year are displayed in blue in square brackets besides the role boxes. The mandatory role constraint and the uniqueness constraints ensure that each scientist was born in exactly one year and died in at most one year.

The circled ">" with an arrow directed from the deathYear role to the birthyear role depicts a value-comparison constraint. In ORM, a value-comparison constraint may be used to compare one value with another using one of the following six comparison operators: <, ≤, >, ≥, =, ≠. The two dots on the left and right of the enclosing circle indicate that two instances are being compared rather than two sets. In this example, the ">" comparator is used. The NORMA tool verbalizes this value-comparison constraint as follows: "For each Scientist, if that Scientist died in some Year₁ and was born in some Year₂ then Year₁ is greater than Year₂." Neither ER nor UML support a graphic notation for value-comparison constraints, so will be ignored for the rest of this section.

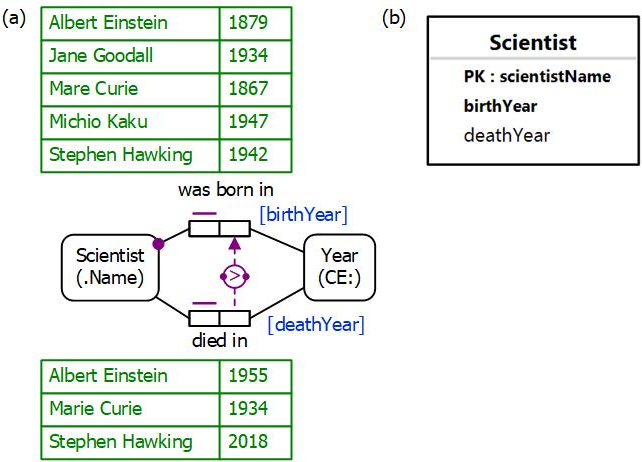
Figure 7. (a) A populated ORM model for Table 1, and (b) a simplified relational database schema for the example.

Figure 7(b) shows the relational database schema diagram generated by the NORMA tool for this example. The primary key is marked "PK", and non-null attributes are displayed in bold. The value-comparison constraint is not depicted in this relational view, but when mapped to SQL, the value-comparison constraint may be enforced by the simple check clause check(deathYear > birthyear) on the Scientist table. Since SQL check clauses are violated only when they evaluate to False, the constraint is correctly enforced even when the deathYear entry is a null value.

The ORM schema in Figure 7(a) may be coded in LogiQL as follows. You can store year values using one of LogiQL's datetime datatypes (see the link to the Core Reference manual in the conclusion), but for simplicity let's just store the year numbers as integers.

Scientist(s), hasScientistName(s:sn) -> string(sn).
birthYearOf[s] = yr -> Scientist(s), int(yr).
deathYearOf[s] = yr -> Scientist(s), int(yr).
// Each scientist was born in some year
Scientist(s) -> birthYearOf[s] = _.
// For each scientist with a birth year and a death year, deathYear > birthYear
birthYearOf[s] = _, deathYearOf[s] = _ -> deathYearOf[s] > birthYearOf[s].

The data may be entered in LogiQL using the following delta rules:

+Scientist(s1), +hasScientistName(s1:"Albert Einstein"), + birthYearOf[s1]=1879, + deathYearOf[s1]=1955.
+Scientist(s2), +hasScientistName(s2:"Jane Goodall"), + birthYearOf[s2]=1934.
+Scientist(s3), +hasScientistName(s3:"Marie Curie"), + birthYearOf[s3]=1867, + deathYearOf[s3]=1934.
+Scientist(s4), +hasScientistName(s4:"Michio Kakul"), + birthYearOf[s4]=1947.
+Scientist(s5), +hasScientistName(s5:"Stephen Hawking"), + birthYearOf[s5]=1942, + deathYearOf[s5]=2018.

If you enter the above schema and data, and then execute the following query to list the name and birth year of those scientists born in a year when some scientist died, you will get result shown in Figure 8.

_(sn, by) <- hasScientistName(s:sn), birthYearOf[s] = by, deathYearOf[_] = by.

Figure 8. A query to list the name and birth year of each scientist who was born in a year some scientist died.

Conclusion

The current article discussed how to declare object cardinality constraints, role cardinality constraints, and value-comparison constraints in ORM and LogiQL. The core reference manual for LogiQL is accessible at https://developer.logicblox.com/content/docs4/core-reference/. An introductory tutorial for LogiQL and the REPL tool is available at https://developer.logicblox.com/content/docs4/tutorial/repl/section/split.html. Further coverage of LogiQL may be found in [21].

References

1. Abiteboul, S., Hull, R. & Vianu, V. 1995, Foundations of Databases, Addison-Wesley, Reading, MA.


2. Aref, M., Cate, B., Green T., Kimefeld, B., Olteanu, D., Pasalic, E., Veldhuizen, T. & Washburn, G. 2015, 'Design and Implementation of the LogicBlox System', Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York. http://dx.doi.org/10.1145/2723372.2742796


3. Barker, R. 1990, CASE*Method: Entity Relationship Modelling, Addison-Wesley, Wokingham.


4. Curland, M. & Halpin, T. 2010, 'The NORMA Software Tool for ORM 2', P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, pp. 190-204, Springer-Verlag Berlin Heidelberg 2010.


5. Halpin, T. 2014, "Logical Data Modeling: Part 1," Business Rules Journal, Vol. 15, No. 5 (May, 2014), URL: http://www.BRCommunity.com/a2014/b760.html


6. Halpin, T. 2014, "Logical Data Modeling: Part 2," Business Rules Journal, Vol. 15, No. 10 (Oct., 2014), URL: http://www.BRCommunity.com/a2014/b780.html


7. Halpin, T. 2015, "Logical Data Modeling: Part 3," Business Rules Journal, Vol. 16, No. 1 (Jan., 2015), URL: http://www.BRCommunity.com/a2015/b795.html


8. Halpin, T. 2015, "Logical Data Modeling: Part 4," Business Rules Journal, Vol. 16, No. 7 (July, 2015), URL: http://www.BRCommunity.com/a2015/b820.html


9. Halpin, T. 2015, "Logical Data Modeling: Part 5," Business Rules Journal, Vol. 16, No. 10 (Oct., 2015), URL: http://www.BRCommunity.com/a2015/b832.html


10. Halpin, T. 2016, "Logical Data Modeling: Part 6," Business Rules Journal, Vol. 17, No. 3 Mar., 2016), URL: http://www.BRCommunity.com/a2016/b852.html


11. Halpin, T. 2016, "Logical Data Modeling: Part 7," Business Rules Journal, Vol. 17, No. 7 (July, 2016), URL: http://www.brcommunity.com/a2016/b866.html


12. Halpin, T. 2016, "Logical Data Modeling: Part 8," Business Rules Journal, Vol. 17, No. 11 (Nov, 2016), URL: http://www.brcommunity.com/a2016/b883.html


13. Halpin, T. 2017, "Logical Data Modeling: Part 9," Business Rules Journal, Vol. 18, No. 5 (May, 2017), URL: http://www.brcommunity.com/a2017/b906.html


14. Halpin, T. 2017, "Logical Data Modeling: Part 10," Business Rules Journal, Vol. 18, No. 11 (Nov, 2017), URL: http://www.brcommunity.com/a2017/b929.html


15. Halpin, T. 2018, "Logical Data Modeling: Part 11," Business Rules Journal, Vol. 19, No. 4 (April, 2018), URL: http://www.brcommunity.com/a2018/b949.html


16. Halpin, T. 2018, "Logical Data Modeling: Part 12," Business Rules Journal, Vol. 19, No. 7 (July, 2018), URL: http://www.brcommunity.com/a2018/b960.html


17. Halpin, T. 2018, "Logical Data Modeling: Part 13," Business Rules Journal, Vol. 19, No. 10 (Oct., 2018), URL: http://www.brcommunity.com/a2018/b971.html


18. Halpin, T. 2015, Object-Role Modeling Fundamentals, Technics Publications, New Jersey.


19. Halpin, T. 2016, Object-Role Modeling Workbook, Technics Publications, New Jersey.


20. Halpin, T. & Morgan, T. 2008, Information Modeling and Relational Databases, 2^nd edition, Morgan Kaufmann, San Francisco.


21. Halpin, T. & Rugaber, S. 2014, LogiQL: A Query language for Smart Databases, CRC Press, Boca Raton. http://www.crcpress.com/product/isbn/9781482244939#


22. Halpin, T. & Wijbenga, J. 2010, 'FORML 2', Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg, pp. 247-260.


23. Huang, S., Green, T. & Loo, B. 2011, 'Datalog and emerging applications: an interactive tutorial', Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York. http://dl.acm.org/citation.cfm?id=1989456


24. Object Management Group 2017, OMG Unified Modeling Language (OMG UML), version 2.5.1. Retrieved from http://www.omg.org/spec/UML/2.5.1/


25. OMG, 2012, OMG Object Constraint Language (OCL), version 2.3.1. Retrieved from http://www.omg.org/spec/OCL/2.3.1/

# # #