Verbalizing Business Rules (Part 9)
Business rules should be validated by business domain experts, and hence specified using concepts and languages easily understood by business people. This is the ninth in a series of articles on expressing business rules formally in a high-level, textual language. This article discusses verbalization of exclusion constraints.
The first article[4] discussed criteria for a business rules language, and verbalization of simple uniqueness and mandatory constraints on binary associations. Article two[5] examined hyphen-binding, and verbalization of internal uniqueness constraints that span a whole association, or that apply to n-ary associations. Article three[6] covered verbalization of basic external uniqueness constraints. The fourth article[7] considered relational-style verbalization of external uniqueness constraints involving nesting or long join paths, as well as attribute-style verbalization of uniqueness constraints and simple mandatory constraints. Article five[8] discussed verbalization of mandatory constraints on roles of n-ary associations, and disjunctive mandatory constraints (also known as inclusive-or constraints) over sets of roles. The sixth article[9] considered verbalization of value constraints. The seventh article[10] examined verbalization of subset constraints. Article eight[11] discussed verbalization of equality constraints.
Verbalization of exclusion constraints between single roles
Figure 1 shows an ORM schema for recording when an application is submitted, and
optionally when it is approved or rejected. The circled 'X'
connecting the approval and rejection roles played by Application indicates that for each state of
the business domain, the population of these two roles is mutually exclusive.
In other words, if we record the fact that an application was approved on some date,
we cannot at the same time record the fact that that application was also rejected
on some (possibly other) date. This illustrates a simple exclusion constraint
between two fact type roles. An exclusion constraint may be applied only if
the roles are compatible (i.e., based on identical or overlapping types).
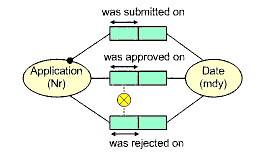
Figure 1. An exclusion constraint between
single roles.
Like all the constraints considered previously, the exclusion constraint is a static constraint, not a dynamic constraint. This schema allows that a rejected application might be re-evaluated and approved, so long as the previous rejection fact is deleted in the same (conceptual) transaction as the addition of the approval fact. Suppose instead we require that if an application is rejected, it cannot be re-evaluated and accepted (a new application must be submitted if approval is still sought). This further requirement applies a dynamic restriction that goes beyond the simple exclusion constraint (e.g., we might require that any approval or rejection fact be frozen). A treatment of dynamic constraints is postponed till a later article.
The static exclusion constraint may be formally verbalized in any of the following ways. The wording reflects the static nature of the constraint, restricting what is (conceptually) recorded in any business state.
No Application that was approved on a Date also was rejected on a Date.For each Application, at most one of the following is true:that Application was approved on a Date;that Application was rejected on a Date.
In the first verbalization, the word 'also'
is optional. The second verbalization should be used if the exclusion constraint
applies to more than two roles. As usual, the pronoun 'that'
may be replaced by 'who'
or 'which', the quantifier
'a' may be replaced by
'some', 'at least one', or 'an',
and 'for each' may be replaced
by 'given any'.
Figure 2(b) shows a UML class diagram for the application example. The '{P}' annotation is a non-standard extension
to UML to express the preferred identifier (and hence its uniqueness constraint).
As there is no graphic way of depicting the exclusion constraint in UML, it is expressed
in OCL within an attached note. Because the note is attached to the Application class, this is understood to provide
the context for the OCL constraint.
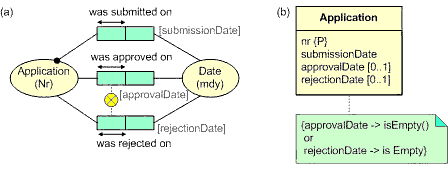
Figure 2. The Figure 1 schema expressed as (a) ORM schema with role names, (b) UML class diagram.
As the OCL specification is too mathematical in nature for non-technical domain experts, a higher-level verbalization is required for the exclusion constraint, such as the relational-style verbalization given earlier. The following attribute-style verbalizations may also be used. These alternative verbalizations may also be applied to the ORM schema, so long as the relevant role names are added, as in Figure 2(a).
For each Application:approvalDate is absent or rejectionDate is absent.For each Application, at most one of the following exists:approvalDate;rejectionDate.
An n-ary version of an exclusion constraint may be applied to a set of three or more compatible roles (or role-sequences). This is equivalent to multiple binary exclusion constraints between all the pairs of roles (or role-sequences).
Verbalization of exclusive-or constraints
In some cases, if an exclusion constraint applies between single roles, then so does an inclusive-or constraint (see [8]). In this case, the combination of both constraints is known as an exclusive-or constraint. A simple example is shown in Figure 3, declaring that each person is a male or female but not both. ORM allows the two constraints to be either combined orthogonally for display purposes, or displayed separately, as shown.
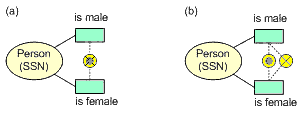
Figure 3. An exclusive-or constraint combines
an inclusive-or constraint with an exclusion constraint.
Internally, the exclusive-or constraint is treated as two constraints (allowing one to be dropped without the other). It may be verbalized as two separate constraints (using patterns discussed previously for inclusive-or and exclusion), or more compactly as a single constraint as follows.
Each Person is male or is female but not both.For each Person, exactly one of the following is true:that Person is male;that Person is female.
Figure 4 shows three different ways of modeling the example in UML. In Figure
4(a) the is-male and is-female predicates are modeled by optional
Boolean attributes. As discussed next, UML does have a graphical exclusive-or
constraint, but it is defined between associations, not attributes. So here
the exclusive-or constraint is specified as a note in OCL. The ORM verbalizations
given above provide a less technical verbalization. Figure 4(b) models the
situation with one mandatory Boolean attribute (isMale),
using the setting isMale = false
to capture is-female. Figure
4(c) uses an association to an enumeration type for the two sex values.
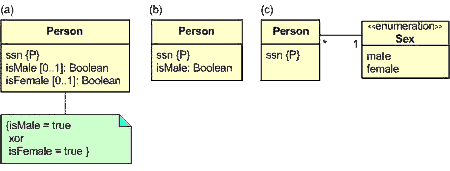
Figure 4. Different ways of modeling the
previous schema in UML.
UML provides a graphical exclusive-or constraint between associations,
attaching '{xor}' to a dotted
line between the relevant associations. As explained earlier however, an xor
constraint only makes sense between compatible association roles. Using
the UML notation, one may deduce the intended roles for the constraint if these roles
occur in binary associations, are played by the same class, and the other roles are
played by two different classes (e.g., Account
is owned by Person xor Account is owned by Organization).
If the other roles are played by the same class however, the notation is ambiguous. For example, consider the ORM schema in Figure 5(a). The exclusive-or constraint declares that each vehicle was either purchased (from some company) or leased (from some company) but not both. Now look at the UML class diagram in Figure 5(b). Here the xor constraint is declared between the two associations, not between roles. We have no formal way to determine which roles are intended, so the constraint must be disambiguated by an additional textual constraint, here specified in OCL within a note. Even with this note, it is unclear whether the note is there to disambiguate the graphical xor constraint, or to add a second xor constraint. It is best to never display UML's graphical xor constraint in such cases, as the wrong interpretation might be taken. Unfortunately, this fundamental problem with the semantics of UML's xor constraint is still present in the latest version (UML 2.0). For validation with domain experts, a high level verbalization is safest.
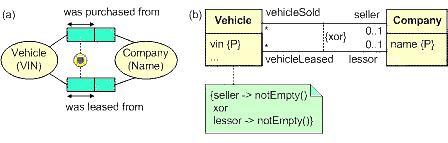
Figure 5. An xor constraint in ORM that
is graphically ambiguous in UML.
Verbalization of exclusion constraints between role sequences
Exclusion constraints may also be specified between compatible role sequences (of two or more roles). Figure 6 shows an ORM schema for a simple example, where each role sequence is a pair of roles comprising a full association. The constraint indicates that nobody may author and review the same book.
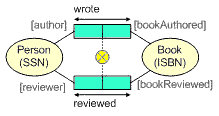
Figure 6. An exclusion constraint between
two role-sequences, each of which contains 2 roles.
This pair-exclusion constraint may be verbalized in relational style as follows. The second and third alternatives scale easily to cases with more than two role-sequences. The third case caters best for cases where the same object type plays more than one role in the role sequence.
No Person wrote and reviewed the same Book.For each Person and Book, at most one of the following is true:that Person wrote that Book;that Person reviewed that BookFor each Person1 and Book1, at most one of the following is true:Person1 wrote Book1 ;Person1 reviewed Book1.
If inverse readings are supplied for the fact types, these may be used to provide
alternative verbalizations, e.g., No
Book was written by and reviewed by the same Person.
Attribute-style verbalizations may be obtained by using role names. The use
of singular names for the roles does not imply single-valued results (e.g., for each
person, bookAuthored and bookReviewed each return a set).
The attribute-style verbalizations differ depending on which object type is used
as the base of the verbalization. For example, starting with Person we may verbalize the exclusion constraint
thus:
For each Person, the following sets are disjoint:bookAuthored;bookReviewed.
Figure 7 depicts the same example in UML. As UML has no graphical exclusion
constraint (except within an xor constraint), the exclusion constraint must be specified
textually. Here rather than using OCL, the constraint is informally expressed
as a note attached to the Person
class. Alternatively, the constraint could have been expressed by a note attached
to the Book class (author intersect reviewer = { }), or by a note
attached to both the associations.

Figure 7. The previous example modeled
in UML, with the exclusion constraint expressed informally.
Conceptually, the exclusion constraint under consideration applies between two associations, regardless of whether we verbalize it directly in terms of the associations, or base it on a class or object type at one end, using attribute-style wording. If the m:n conceptual fact types are implemented as relation schemes in a relational database system, then the constraint needs to be checked on insert or update to either relation scheme. If the conceptual fact types are implemented as pointer sets in a class model, the constraint needs to be checked on creation or update of objects in each class. Such implementation details are irrelevant to validating the business rule with the domain expert, who simply confirms whether the high-level verbalization accurately captures the semantics of the business constraint.
The verbalization patterns discussed above for exclusion constraints may be extended in obvious ways to cater for other cases, where each role-sequence may contain more than two roles from all or part of an association, or is projected from a role path spanning multiple associations.
That completes our coverage of exclusion constraints and their verbalization. The next article considers frequency and ring constraints.
References
[1] T.A. Halpin. Information Modeling and Relational Databases. Morgan Kaufmann, San Francisco, 2001.
[2] T.A. Halpin. "Join Constraints," Proc. EMMSAD'02: 7th Int. IFIP WG8.1 Workshop on Evaluation of Modeling Methods in Systems Analysis and Design. Toronto, (June, 2002). Available online at http://www.orm.net/pdf/JoinConstraints.pdf
[3] T.A. Halpin. "Metaschemas for ER, ORM and UML Data Models: A Comparison," Journal of Database Management, Vol. 13, No. 2 (2002), pp. 20-29. Idea Publishing Group, Hershey, PA, USA.
[4] T.A. Halpin. "Verbalizing Business Rules
(part 1)," Business Rules Journal, Vol. 4, No. 4 (April 2003).
URL: http://www.BRCommunity.com/a2003/b138.html ![]()
[5] T.A. Halpin. "Verbalizing Business Rules
(part 2)," Business Rules Journal, Vol. 4, No. 6 (June 2003). URL: http://www.BRCommunity.com/a2003/b152.html ![]()
[6] T.A. Halpin. "Verbalizing Business Rules
(part 3)," Business Rules Journal, Vol. 4, No. 8 (August 2003).
URL: http://www.BRCommunity.com/a2003/b163.html ![]()
[7] T.A. Halpin. "Verbalizing Business Rules
(part 4)," Business Rules Journal, Vol. 4, No. 10 (October 2003).
URL: http://www.BRCommunity.com/a2003/b172.html ![]()
[8] T.A. Halpin. "Verbalizing Business Rules
(part 5)," Business Rules Journal, Vol. 5, No. 2 (February 2004).
URL: http://www.BRCommunity.com/a2004/b179.html ![]()
[9] T.A. Halpin. "Verbalizing Business Rules
(part 6)," Business Rules Journal, Vol. 5, No. 4 (April 2004).
URL: http://www.BRCommunity.com/a2004/b183.html ![]()
[10] T.A. Halpin. "Verbalizing Business Rules
(part 7)," Business Rules Journal, Vol. 5, No. 7 (July 2004). URL: http://www.BRCommunity.com/a2004/b198.html ![]()
[11] T.A. Halpin. "Verbalizing Business Rules
(part 8)," Business Rules Journal, Vol. 5, No. 8 (September 2004).
URL: http://www.BRCommunity.com/a2004/b205.html ![]()
[12] T.A. Halpin, K. Evans, P. Hallock, & B. MacLean. Database Modeling with Microsoft Visio for Enterprise Architects. Morgan Kaufmann, San Francisco, 2003.
[13] Object Management Group. UML 2.0 Infrastructure. Object Management Group, 2003. URL: http://www.omg.org/uml
[14] Object Management Group. UML 2.0 Object Constraint Language. Object Management Group, 2003. URL: http://www.omg.org/uml
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules