Verbalizing Business Rules (Part 14)
Business rules should be validated by business domain experts, and hence specified in a language easily understood by business people. This is the fourteenth in a series of articles on expressing business rules formally in a high-level, textual language. This article discusses why subtype definitions are needed, and how to verbalize them.
The first article[3] discussed criteria for a business rules language, and verbalization of simple uniqueness and mandatory constraints on binary associations. Article two[4] examined hyphen-binding, and verbalization of internal uniqueness constraints that span a whole association, or that apply to n-ary associations. Article three[5] covered verbalization of basic external uniqueness constraints. Article four[6] considered relational-style verbalization of external uniqueness constraints involving nesting or long join paths, as well as attribute-style verbalization of uniqueness constraints and simple mandatory constraints. Article five[7] discussed verbalization of mandatory constraints on roles of n-ary associations, and disjunctive mandatory constraints (also known as inclusive-or constraints) over sets of roles.
Article six[8] considered verbalization of value constraints. Article seven[9] examined verbalization of subset constraints. Article eight[10] discussed verbalization of equality constraints. Article nine[11] covered verbalization of exclusion constraints. Article ten[12] dealt with verbalization of internal frequency constraints on single roles. Article eleven[13] considered verbalization of multi-role, and external, frequency constraints. Article twelve[14] discussed verbalization of ring constraints. Article thirteen[15] covered verbalization of basic subtype constraints.
Why Subtype?
There are three main reasons for including subtyping in an information model. The most important reason is to constrain certain roles to be played only by specific subtypes. For example, in a hospital domain, prostate status may be recorded only for male patients, and pregnancy counts (number of pregnancies) may be recorded only for female patients. Figure 1 depicts this situation in ORM 2[16], UML[18], and Barker ER[1] notations.
Figure 1.
MalePatientandFemalePatientsubtypes in (a) ORM2, (b) UML, and (c) Barker ER notation.
The {P} notation in the UML figure is a non-standard extension indicating preferred identification scheme (and hence mandatory and unique). Previous articles used the ORM notation supported in Microsoft Visio for Enterprise Architects.[17] ORM 2 is a second generation version of ORM supported in the Neumont ORM Architect (NORMA) tool, an open source plug-in to Visual Studio .NET 2005. As an early prototype of NORMA should be released by the time this article is published, and ORM 2 incorporates significant advances over ORM 1, the ORM 2 notation will be used in this and future articles in this series. As indicated in Figure 1(a), ORM 2 diagrams no longer use arrow tips on uniqueness constraint bars, and object type names are enclosed by default in rounded rectangles rather than ellipses (as a configuration option, ellipses or hard rectangles may also be used). ORM 2 diagrams are also more compact than corresponding ORM 1 diagrams.
A second reason for including subtyping is to explicitly display taxonomy,
by displaying categories resulting from a classification scheme. In
our current example, gender is used to classify patients into male and female patients.
For such cases, taxonomy may be modeled more compactly without subtyping, simply
by declaring the relevant fact type in the classification scheme (here Patient
is of Gender), together with a listing of the possible values of the relevant
value type value (here GenderCode) by declaring a value constraint (here
{'M', 'F'}) or by entering them in the type's population
(if the number of instances is large or variable).
In some cases, this is the only practical way to declare a classification scheme.
For example, there are hundreds of different kinds of animal. It is far more
efficient and compact to enter these by populating AnimalKind in the
fact type Animal is of AnimalKind, than by explicitly introducing hundreds
of subtypes for Dog, Cat, Kangaroo, etc. Of course, if there are some specific
roles of interest for a few specific subtypes, we would normally introduce just those
few subtypes.
A third reason for introducing subtypes is to facilitate reuse of model components,
thus leading to efficiency gains in representation and implementation. For
example, if we want to know details such as name, gender, address, and phone number
for both male and female patients, it is more convenient to attach these details
to the supertype Patient, from which MalePatient and FemalePatient
inherit, rather than attach them directly to MalePatient and FemalePatient.
Subtype Discriminators and the Need for Subtype Definitions
The schema under discussion requires that each patient has exactly one of two
genders, referenced by the gender codes "M" and "F", each male
patient has at most one prostate status, referenced by a description (e.g., "OK",
"benign enlargement"), and each female patient has exactly one pregnancy
count, referenced by a whole number (0, 1, 2, etc.). As discussed in the previous
article [15], the subtyping constraints in all three
notations ensure that MalePatient and FemalePatient are
mutually exclusive and collectively exhaustive of Patient (i.e., they
form a partition of Patient).
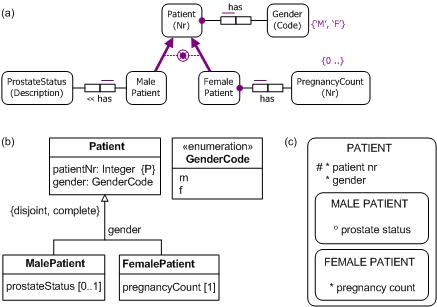
For discussion purposes, suppose the schema is populated with five facts, as shown in the ORM model in Figure 2. Here patients 101 and 103 are male, patient 102 is female, patient 102 has a prostate status of OK, and patients 101 and 103 have each had four pregnancies. Notice that this population satisfies all the constraints. But there is still something wrong. What is the problem?
Figure 2. The constraints are satisfied, but there is still a problem with the population.
You no doubt spotted that the population incorrectly assigns a prostate status
to the female patient, while assigning a pregnancy count to the male patients.
This nonsensical situation is allowed by the schema, because the schema currently
provides no formal connection between the classification fact type (Patient
has Gender) and the subtypes (MalePatient and FemalePatient).
This is the case not just for the ORM schema, but also for
the UML and Barker ER schemas. The UML schema in Figure 1(b) goes part of the
way by including gender as a discriminator on the subtype graph. Though
not supported in Barker ER, discriminators are supported in some other versions of
ER as well as the ER-relational hybrid IDEF1X (e.g., see [2] p.
342). The gender discriminator informally enables a human reader to
understand that patients are being classified into subtypes on the basis of gender,
and humans may use their background knowledge to associate the name 'MalePatient'
with the gender code 'm' and the name 'FemalePatient' with the gender
code 'f'. But the UML schema provides no formal specification of this understanding,
so without further information a computer would still accept the population shown.
In cases like this, where both the classification fact type(s) and related subtypes are included in the schema, the only solution to this problem is to require formal definitions for subtypes, thus establishing the required formal connection. Of the three approaches mentioned, only ORM stipulates this requirement as part of its modeling procedure, and only ORM requires that such definitions be verbalized at a high enough level to be readily understood by non-technical domain experts. In ORM the subtype definitions are normally verbalized thus:
EachMalePatient is a Patient who is of Gender 'M'
EachFemalePatient is a Patient who is of Gender 'F'
The pronoun 'who' is used if Patient is declared to be a personal
object type; otherwise 'that' is used. If desired, the
verbose form of the gender reference may be used. For example, "Gender
'M'" may be automatically unabbreviated to "Gender that
has GenderCode 'M'".
Once such definitions are supplied and formally interpreted, the population shown
in Figure 2 must be rejected since it violates the schema (which now includes the
subtype definitions, typically displayed below the diagram). Notice also that
the subtype exclusion and totality constraints displayed in the schema are now implied
by the subtype definitions, in conjunction with the constraints on the defining fact
type (Patient is of Gender). Given the subtype definitions, the
mandatory constraint and value constraint imply subtype totality, and the uniqueness
constraint implies that the subtypes are mutually exclusive. For this reason,
display of subtype totality and exclusion constraints is optional in ORM, when subtype
definitions are declared.
Though not required in UML, one could extend that approach by requiring subtype definitions for cases like our patient example. UML already provides OCL[19] as a language that could be used to express subtype definitions formally. However OCL expressions are often too mathematical in nature to be readily understood by non-technical business people, so we recommend that ORM-like verbalizations be used instead (for which a transform could be provided to map to OCL if desired).
Three Kinds of Subtype
In ORM 1, the modeling procedure requires that all subtypes be formally and fully defined in terms of roles played by their supertype(s). In ORM 2, this requirement has been relaxed to allow three kinds of subtypes: asserted, fully-derived, and partly-derived.
An asserted subtype is one for which no subtype definition is provided -- one
merely asserts the existence of the subtype without defining it in terms of something
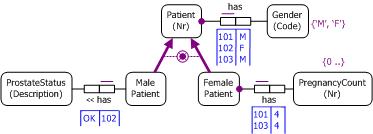
else. For example, suppose that for some reason we do not want to include
Patient is of Gender as a base fact type. Figure 3 illustrates
this situation in all three notations. In such a case, the totality and exclusion
subtyping constraints must be declared, since they are no longer implied, and they
may be verbalized as discussed in the previous article[15].
Although this example is somewhat contrived, since gender is normally recorded
explicitly in such a case, it is common practice to do this kind of thing in programming,
especially where the superclass is declared abstract. However, the notion of
subclass in programming is sub-conceptual. Instead of meaning subtype in the
conceptual sense, a subclass is basically a "factory" for creating instances,
and since instances can be created in only one factory, migration between subclasses
is not possible. In contrast, migration between subtypes is allowed for those
subtypes that do correspond to fundamental sortals (e.g., a person who is an instance
of InPatient might migrate later to become an instance of OutPatient).
Figure 3. Asserted subtypes in (a) ORM 2, (b) UML and (c) Barker ER.
In addition to asserted subtypes, ORM 2 allows fully-derived subtypes (full subtype definition provided) and partly-derived subtypes (partial subtype definition provided). Subtype definitions are supported as derivation rules in a high level formal language, and may be displayed in text boxes as footnotes on the diagram. The formal grammar and precise syntax for ORM 2's formal textual input language (as distinct from its output verbalization language) is still being refined, but the following examples are indicative. Equivalence (if and only if) rules are used for full derivation, and implication (if) rules for partial derivation. Here are sample rules in both ORM 2's textual language and predicate logic for fully and partly derived subtypes respectively:
EachAustralian is a Person who was born in Country 'AU'.x[Australian x(Person x &
y:Country
z:CountryCode (x was born in y & y has z & z = 'AU'))]
Person1 is a Grandparent if Person1 is a parent of some Person2 who is a parent of some Person3.x:Person [Grandparent x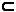
y:Person
z:Person (x is a parent of y & y is a parent of z)]
Expressing such definitions formally, instead of as mere comments, ensures they are unambiguous, and makes it possible to generate code automatically to enforce the constraints captured by the definitions.
Subtype Definitions involving Multiple Fact Types
In modeling complex business domains, one often encounters subtyping schemes where
a subtype is defined using multiple fact types. In such cases, the subtype
definitions are not readily expressible using the simple discriminator approach mentioned
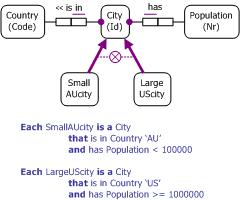
earlier. Figure 4 shows a simple example, with the subtype definitions below
the diagram. In general, subtype definitions may be of arbitrary complexity,
and (as in our earlier Patient example) the constraints that they express
cannot be fully captured by simple totality and exclusion constraints.
Figure 4. Subtype definitions involving multiple fact types.
References
[1] R. Barker. CASE*Method: Tasks and Deliverables.
Addison-Wesley: Wokingham, England, 1990. ![]()
[2] T.A. Halpin. Information Modeling and Relational
Databases. Morgan Kaufmann: San Francisco, 2001. ![]()
[3] T.A. Halpin. "Verbalizing Business Rules
(Part 1)," Business Rules Journal, Vol. 4, No. 4 (April 2003).
URL: http://www.BRCommunity.com/a2003/b138.html ![]()
[4] T.A. Halpin. "Verbalizing Business Rules
(Part 2)," Business Rules Journal, Vol. 4, No. 6 (June 2003). URL: http://www.BRCommunity.com/a2003/b152.html ![]()
[5] T.A. Halpin. "Verbalizing Business Rules
(Part 3)," Business Rules Journal, Vol. 4, No. 8 (August 2003).
URL: http://www.BRCommunity.com/a2003/b163.html ![]()
[6] T.A. Halpin. "Verbalizing Business Rules
(Part 4)," Business Rules Journal, Vol. 4, No. 10 (October 2003).
URL: http://www.BRCommunity.com/a2003/b172.html ![]()
[7] T.A. Halpin. "Verbalizing Business Rules
(Part 5)," Business Rules Journal, Vol. 5, No. 2 (February 2004).
URL: http://www.BRCommunity.com/a2004/b179.html ![]()
[8] T.A. Halpin. "Verbalizing Business Rules
(Part 6)," Business Rules Journal, Vol. 5, No. 4 (April 2004).
URL: http://www.BRCommunity.com/a2004/b183.html ![]()
[9] T.A. Halpin. "Verbalizing Business Rules
(Part 7)," Business Rules Journal, Vol. 5, No. 7 (July 2004). URL: http://www.BRCommunity.com/a2004/b198.html ![]()
[10] T.A. Halpin. "Verbalizing Business Rules
(Part 8)," Business Rules Journal, Vol. 5, No. 9 (September 2004).
URL: http://www.BRCommunity.com/a2004/b205.html ![]()
[11] T.A. Halpin. "Verbalizing Business Rules
(Part 9)," Business Rules Journal, Vol. 5, No. 12 (December 2004).
URL: http://www.BRCommunity.com/a2004/b215.html ![]()
[12] T.A. Halpin. "Verbalizing Business Rules
(Part 10)," Business Rules Journal, Vol. 6, No. 4 (April 2005).
URL: http://www.BRCommunity.com/a2005/b229.html ![]()
[13] T.A. Halpin. "Verbalizing Business Rules
(Part 11)," Business Rules Journal, Vol. 6, No. 6 (June 2005).
URL: http://www.BRCommunity.com/a2005/b238.html ![]()
[14] T.A. Halpin. "Verbalizing Business Rules
(Part 12)," Business Rules Journal, Vol. 6, No. 10 (October 2005).
URL: http://www.BRCommunity.com/a2005/b252.html ![]()
[15] ] T.A. Halpin. "Verbalizing Business
Rules (Part 13)," Business Rules Journal, Vol. 6, No. 12 (December 2005).
URL: http://www.BRCommunity.com/a2005/b261.html ![]()
[16] T.A. Halpin, "ORM 2," On the Move to
Meaningful Internet Systems 2005: OTM 2005 Workshops, eds. R. Meersman, Z. Tari,
P. Herrero, et al. Cyprus: Springer LNCS 3762, pp. 676-87, 2005. ![]()
[17] T.A. Halpin, K. Evans, P. Hallock, & B. MacLean.
Database Modeling with Microsoft Visio for Enterprise Architects. Morgan
Kaufmann: San Francisco, 2003. ![]()
[18] Object Management Group. UML 2.0 Infrastructure.
Object Management Group, 2003. URL: http://www.omg.org/uml ![]()
[19] Object Management Group. UML 2.0 Object
Constraint Language. Object Management Group, 2003. URL: http://www.omg.org/uml ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules