Improving Decision Table Rules with Data Mining
It is well known in business rules circles that rules engines often execute rules using an inference strategy known as forward chaining, most often implementing this using a rete network. Some problems are, arguably, more suited to a backward chaining strategy and, in some cases, to the combined approach where every rule acts as a demon (opportunistic or mixed chaining). However, there is another mode of inference that is seldom discussed in the context of Business Rules Management Systems (BRMS) and is more commonly the property of the data mining community. In this article, I want to show how this other strategy, rule induction, is related to the idea of decision tables and could be used to enhance the current generation of BRMS.[1]
This other mode of inference is rule induction . Broadly, while backward and forward chaining enable us to infer new facts from rules and data, induction enables us to infer new rules from collections of facts and data. The word 'induction' has two senses: the Aristotelian sense of a syllogism in which the major premise in conjunction with instances entails the generalization, or the sense of empirical generalization from observations. A third sense, the principle of mathematical induction, need not concern us here. It is with the second sense we shall be concerned.
Most authorities talk about induction in terms of probabilities; if we observe that sheep on two hundred hillsides all have wool and four legs, then we may induce the generalization 'all sheep have wool and four legs'. Every observation we then make increases the probability of this statement being true, but never confirms it completely. Only one observation of a shorn, three-legged merino is needed to refute the theory.
From our point of view, this cannot be correct because there are many kinds of uncertainty, and it can be said equally that a degree of knowledge, belief, possibility, or the relevance of the rules is what is changed by experience rather than probability. The obsession with probability derives (probably) from the prevailing empiricist climate in the philosophy of science -- experience being seen only as experiments performed by external observers trying to refute some hypothesis.
Another view is possible. The history of quantum physics shows that we can no longer regard observers as independent from what they observe. Experience takes place in a world of which we humans are an internal part but from which we are able to differentiate ourselves. We do this by internalizing a representation of nature and checking the validity of the representation through continuous practice. However, the very internalization process is a practice, and practice is guided by the representation so far achieved. From this point of view, induction is the process of practice that confirms our existing theories of all kinds. The other important general point to note is that the syllogism of induction moves from the particular to the general, whereas deductive and abductive syllogisms tend to work in the opposite direction -- from the general to the particular.
But to get away from such abstruse concerns, the probabilistic definition of induction does have merit in many cases, especially in the case of new knowledge. It is this case that current computer learning systems always face. In nearly every case, computer programs which reason by induction are presented with a number of examples and expected to find a pattern, generalization, or program that can reproduce and extend the training set.
Suppose we are given the training set of examples shown in Table 1.
Table 1. Training set
NameEye
colourHair
colourSex
Job
J. Stalin
blue
blonde
male
programmer
A. Capone
grey
brown
male
programmer
M. Thatcher
brown
black
female
analyst
R. Kray
brown
brown
male
operator
E. Braune
blue
black
female
analyst
The simplest possible algorithm enables us to infer that:
IF female
THEN analyst
IF male AND (blue eyes OR grey eyes)
THEN programmer
IF brown hair AND brown eyes
THEN operator
However, the addition of a new example (brown eyes, brown hair, female, programmer) makes the position less clear. The first and last rules must be withdrawn, but the second can remain although it no longer has quite the same force.
The first attempts at machine learning came out of the cybernetics movement of the 1950s. Cybernetics, according to its founder Norbert Wiener, is the science of control and communication in animal and machine. Several attempts were made, using primitive technology by today's standards, to build machinery-simulating aspects of animal behaviour. In particular, analogue machines called, by Ross Ashby, homeostats simulated the ability to remain in unstable equilibrium. Perceptrons (two-layer neural nets) are hinted at in Wiener's earliest work on neural networks, and, as the name suggests, were attempts to simulate the functionality of the visual cortex. Learning came in because of the need to classify and recognise physical objects. The technique employed was to weight the input in each of a number of dimensions and, if the resultant vector exceeded a certain threshold, to class the input as a positive example. Neural network technology has now overcome an apparent flaw alleged by Marvin Minsky and Seymour Papert, and impressive learning systems have been built.
Rule-based learning systems also exist. Ross Quinlan's interactive dichotomizer algorithm, known as ID3, selects an arbitrary subset of the training set and partitions it according to the variable with the greatest discriminatory power using an information theoretic measure of the latter; basically minimizing entropy. This is repeated until a new rule is found, which is then added to the rule set as in the above example on jobs. Next the entire training set is searched for exceptions to the new rule and if any are found they are inserted in the sample and the process repeated. The difficulties with this approach are that the end result is a sometimes-huge decision tree which is difficult to understand and modify, and that the algorithm does not do very well in the presence of noisy data, though suitable modifications have been developed based on statistical tests.
One of the problems with totally deterministic algorithms like ID3 is that, although they are guaranteed to find a rule to explain the data in the training set (if one exists), they cannot deal with situations where the rules can only be expressed subject to uncertainty. In complex situations, such as weather forecasting or betting (where only some of the contributory variables can be measured and modelled), often no exact, dichotomizing rules exist. With the simple problem of forecasting whether it will rain tomorrow, it is well known that a reasonably successful rule is 'if it is raining today then it will rain tomorrow'. This is not always true but it is a reasonable approximation for some purposes. ID3 would reject this as a rule if it found one single counter-example. Statistical tests, however useful, require complex independence assumptions and interpretative skills on the part of users.
A completely different class of learning algorithm is based on the concept of adaptation or Darwinian selection. The general idea is to generate rules at random and compute some measure of performance for each rule relative to the training set. Inefficient rules are deleted and operations based on the ideas of mutation, crossover, and inversion are applied to generate new rules. These techniques are referred to as genetic algorithms.
Genetic algorithms are also closely related to neural nets as pattern classification devices. Genetic programming is a form of machine learning that takes a random collection of computer programs and a representation of some problem and then 'evolves' a program that solves the problem. It does this by representing each program as a binary vector, or string, that can be thought of as a chromosome. The chromosomes in each successive sample can 'mate' by crossing over portions of themselves, inverting substrings of their bodies and mutating at random. (Given two binary strings -- representing chromosomes -- 110101 and 111000, their crossover -- at the fourth place -- could either be 110000 or 111101. Crossing over at the first place corresponds to choosing one of the original strings.) Programs that score well against some objective function that represents the problem to be solved are allowed to participate in the next mating round and, after many generations, there is a good chance that a successful -- but not necessarily optimal -- program will evolve.
None of the BRMS products on the market today offers any sort of rule induction facility. However, there are several products on the market that do, and we envisage some benefit from taking the output from such systems and offering the resultant rules to a BRMS.
In all BRMS products, rules are represented as sentences, usually containing the words if and then. Both Ron Ross and Tony Morgan recommend a better style aimed at removing ambiguity, making relationships explicit, avoiding obscure terminology, removing wordiness, and so on. This style is remarkably close to natural language, preferring forms such as
A loan may be approved
if the status of the customer is high and the loan is less than 2000
unless the customer has a low rating
to
if the customer status is high and the loan is less than 2000
and the customer does not have a low rating
then approve the loan
if the customer status is high and the loan is less than 2000
and the customer has a low rating
then don't approve the loan
In some products there are representations alternative to rules. We now consider two of these: decision trees and decision tables.
Decision Trees
Behavioural science has evolved several theories as to how people reach decisions. Such descriptive theories usually conclude by stating that managers do not make decisions on a purely rational basis. To help managers improve their decision making, however, a normative theory such as decision analysis is required.
Decision analysis consists of three principal stages:
- Determine problem structure and objective function (desirable outcome and measure thereof);
- Assess uncertainties and possible outcome states and their consequences;
- Determine a 'best' strategy for achieving a desirable outcome.
A decision problem is characterised as one of selecting one from several options so as to maximise some function of possibly many variables, attributes, or criteria. The naïve formulation is to organize these into a table of options against attributes. Many methods are available to achieve the requisite selection: maximizing, minimaxing, regret, and so on.
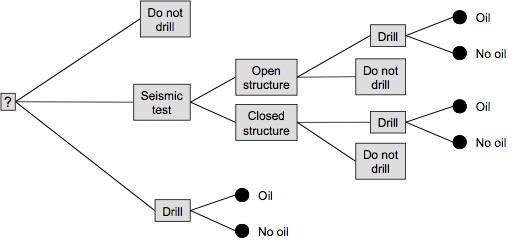
The disadvantage of decision analysis of this kind is that complex problems are sometimes oversimplified by it; a method of overcoming this will be considered in due course. The so-called modelling school of decision analysis would attempt to construct a more explicit model of the relationships, usually as a decision tree such as the one in Figure 1.
In most professions and businesses, decision making takes place in an environment where the cost of obtaining precise information is unjustifiably high. In recognition of this fact the classical theories of decision analysis, operational research, and decision theory make extensive use of normative statistical techniques. The decision problem is either a question of choosing an optimal course of action (such as the ideal mix of ingredients in animal foodstuffs, subject to constraints such as lowest cost and some requisite nutritional value), or it is concerned with generating a plausible set of alternatives. It is the first case that has received most attention.
A decision problem, in this latter sense, is given by stating a set of options, a set of states, a transformation which, to every pair consisting of a state and an option, returns a new state representing the consequence of choosing that option, ceteris paribus. Since the null option (do nothing) is always included, this provides a model of the evolution of the system to which may be added feedback and/or feedforward control of options.
Figure 1. The oilman's problem
Thus, we see that cybernetics becomes a special case of decision theory, and indeed many of the mathematical techniques are held in common. In addition, decision models include a utility function, which represents the ranking of outcomes with regard to their desirability in a given context. This function is analogous to the metrics required for homeostasis in cybernetic systems. In the cases where decisions can be made in the presence of certain data, the techniques of operational research, such as linear and dynamic programming and systems dynamics, are the most commonly used.
This leaves us with essentially only one tool: the decision tree. A decision tree is merely a hierarchy showing the dependencies between decisions. It is a shorthand description of some aspects of the general decision model whose chief value is to clarify our thinking about the consequences of certain decisions being made. However, with the introduction of probabilities, the decision tree becomes a powerful tool.
To see this, consider a very simple example. If one wishes to open a sweet shop, one must decide where it is to be located. There are, let us suppose, three options: near a school in an expensive suburb, in the busy high street, or opposite a playground in a deprived inner city area. Let us call these options A, B, and C. To each of these we can assign a probability of financial success, based on basic cost/revenue calculations and the history of similar ventures. In each case, however, there are other decisions to make, such as how much to invest in stock. Suppose the options and probabilities of success are as displayed in Figure 2, where X, Y, and Z represent these other decisions.
Figure 2. A decision tree with probabilities.
Combining the probabilities shows that option C is the most likely to succeed, despite the fact that, on the basis of the first level of decision, it was the worst option. Exploring the decision tree further might change the position again. Enhancements of this application of probability theory have proved most effective in attacking a wide range of decision problems. It is also possible to use certainty factors in place of probabilities, in which case the arithmetic is different.
In many cases the branches of a tree will be annotated with and followed when particular ranges of values hold for a variable. For example we might set a particular credit limit for a client with annual income in the range 50,000 to 100,000.
Decision Tables
Decision tables represent the same knowledge and rules as decision trees in a tabular format. For example, Table 2 is equivalent to a ruleset stating:
If card type is "Standard"
then discount code is 1
unless age is between 18 and 30If card type is "Standard" and age is between 18 and 30
then discount code is unknownIf card type is "Gold"
then discount code is 2
unless age is between 31 and 40If card type is "Gold" and age is between 31 and 40
then discount code is 1If card type is "Platinum"
then discount code is 3
unless age is between 31 and 40If card type is "Platinum" and age is between 31 and 40
then discount code is 1
We can see that the techniques of rule induction discussed above may be applied to extract the rules from the table automatically. We can also generate a table from a ruleset.
Table 2. A decision table
Min age
Max age
Card type
Discount
code18
30
Standard
18
30
Gold
2
18
30
Platinum
3
31
40
Standard
1
31
40
Gold
1
31
40
Platinum
1
41
50
Standard
1
41
50
Gold
2
41
50
Platinum
3
51
60
Standard
1
51
60
Gold
2
51
60
Platinum
3
61
70
Standard
1
61
70
Gold
2
61
70
Platinum
3
71
120
Standard
1
71
120
Gold
2
71
120
Platinum
3
The main problem with decision tables is that they grow unmanageably large when there is a large number of conditions in the rulebase. Even in the example above, where this is not the case, six rules translate to 72 table entries. Their advantage arises when the organization already holds the knowledge in this form: pricing charts, rate tables, etc.
There is a cruder approach that regards each row in the table as a separate rule, so that row two would correspond to a rule stating:
If card type is "Gold" and age is between 18 and 30
then discount code is 2
Clearly this approach gives us a larger number of rules -- one for each row -- and the rules will be hard to read and understand. We characterize the approach as row-oriented decision tables. Rule subsumption checks may allow the rule author to tidy up the resultant rulesets but, I think, the induction approach is far sounder, potentially. It is better to use a data mining system to extract rules from decision tables and feed them into a BRMS. Less is more.
References
[1] This article is largely excepted from my book Business Rules Management and Service Oriented Architecture (Wiley, 2006). ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.