Temporal Modeling (Part 3)
This is the third in a series of articles on the impact of time on the conceptual modeling of business domains. The first article[6] discussed the temporal data types instant (point in time), interval (duration of time), and period (anchored duration of time), classified temporal object types into once-only (e.g., Date) and repeatable (e.g., WeekDay) object types, and discussed four kinds of fact type: definitional (truth of instances is a matter of definition), once-only (instances correspond to a single event), repeatable (instances may correspond to multiple events), and time-deictic (the meaning of instances depends on the time of utterance/inscription). It then showed how to model temporal details about point events or period events underlying instances of once-only fact types that are unchangeable. The second article[7] examined the modeling of temporal information about events underlying changeable fact types (their non-null fact populations may change over time, by replacing, adding, or deleting facts) that are initially functional (n:1 or 1:1 associations).
The focus of this third article is on maintaining history of changeable fact types that are non-functional (e.g. m:n binaries, or higher arity fact types). Three graphical notations are used for examples: second generation Object-Role Modeling (ORM 2)[4] [5] as supported by the open source (Neumont ORM Architect) NORMA tool[3] [8]; the Unified Modeling Language (UML)[9]; and the Barker notation[1] for Entity-Relationship Modeling (ER)[2].
Maintaining History of Non-functional, Changeable Fact Types
Figure 1 shows a number of ways one might try to model visits of employees to countries, assuming that we know the start date for each visit. Since some visits might still be in progress, an end date for a visit is optional. Figure 1(a) models Visit as an objectified association in ORM, and Figure 1(b) takes a similar approach in UML, modeling Visit as an association class. The "{P}" notation is a non-standard extension to UML to indicate a primary identifier.
As an alternative, Figure 1(c) models Visit as a co-referenced entity type in ORM. The circled double-bar depicts a preferred, external uniqueness constraint, indicating that any instance of Visit may be identified by combining the employee visitor with the country visited. Figure 1(d) takes a similar approach in UML, modeling Visit as a Class with associations to Employee and Country. Since UML has no graphical way to depict an external uniqueness constraint, this constraint is captured in a note.
Figure 1(e) adopts a similar approach to the class diagram in Figure 1(d), but uses the Barker ER notation. The strokes "|" on the association lines indicates that these associations with Employee and Country provide the primary identifier for Visit. Unlike ORM and UML, Barker ER does not support objectification, so it has no analog to the (a) and (b) models.
These models are similar to ones discussed in an earlier article [6]. It should be obvious however, that all of these models have a potential problem. You might like to identify this problem for yourself before reading on.
The main difference between the ORM model in Figure 1(a) and examples in earlier articles is that the fact type Employee visited Country is non-functional (in this case m:n) and repeatable. For example, I have visited Belgium several times. Suppose my employee number is 1001. The fact instance Employee '1001' visited Country 'BE' may be repeated, with one occurrence for each of my visits to Belgium. But the uniqueness constraint spanning the roles of the fact type Employee visited Country requires that such a fact instance appears at most once in any population of the fact type. In other words the model in Figure 1(a) has no way to record multiple visits to the same country by the same employee. The same is true of all the other variations in Figure 1 -- they wrongly assume that a visit may be identified simply by combining the visitor with the country visited. If we are not interested in recording repeated visits, then no change is needed. But suppose we do want to record a full history of visits. How do we do this? Try answering this yourself before reading on.
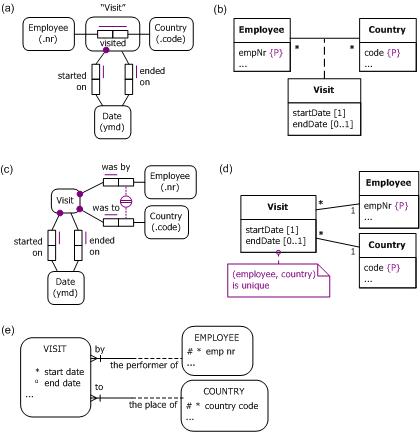
Figure 1. Some attempts to model visits in (a) ORM, (b) UML, (c) ORM, (d) UML, and (e) Barker ER.
There are at least three ways to resolve this problem. The first approach is to include a distinguishing temporal role as part of the identifier. For example, assuming that each employee starts to visit at most one country on any given date, we may identify a visit by combining the visitor, the country visited, and the start date of the visit. The ORM solutions are now remodeled as shown in Figure 2. The additional external uniqueness constraint (circled bar) indicates that where a visit end date exists, each combination of visitor, country visited, and end date applies to at most one visit.
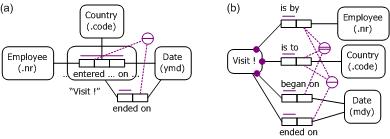
Figure 2. ORM models including start date as part of the identifier for Visit.
The UML and Barker ER versions of the co-referenced approach in Figure 2(b) are shown in Figure 3. UML has no graphic for either external uniqueness constraint so these are captured informally in a note. They could be specified formally in UML's Object Constraint Language (OCL)[10] but the formulae are likely to be unintelligible to non-technical domain experts. The Barker ER version uses an octothorpe "#" to include start-date in the primary identifier, but has no way to specify the external uniqueness constraint involving end-date.
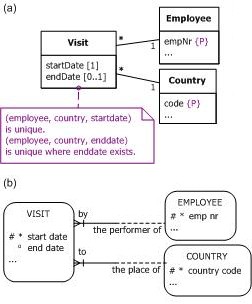
Figure 3. UML and Barker ER models including start date as part of the identifier for Visit.
If an employee may start to visit more than one country on the same date, we need to refine the temporal granularity (e.g., to hour or minute, instead of date) to provide an appropriate visit identifier. The models in Figure 4 choose a granularity of minute. For the rest of the discussion we return to Date, assuming a temporal granularity of one day is sufficient.
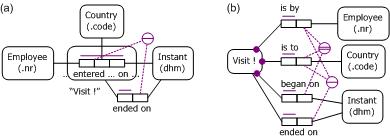
Figure 4. Refining the temporal granularity to minute.
A second approach is to introduce a simple, visible identifier for Visit, as shown in Figure 5. Of course, both of the former external uniqueness constraints still apply, but neither provides the preferred identifier (see the ORM model in Figure 5(a)).
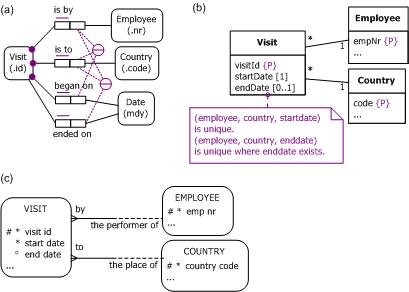
Figure 5. Introducing a simple, visible identifier in (a) ORM, (b) UML, and (c) Barker ER.
In UML, hidden surrogate identifiers are assumed for all objects in all classes. However, we use visitId here as a visible identifier that is used by humans in the business domain to communicate about visits. This requires the addition of a visitId attribute to the UML solution as shown in Figure 5(b). Again, the non-standard "{P}" notation is used to indicate the primary identifier.
In the Barker ER solution (Figure 5(c)), a visit-id attribute is added, with "#" marking it as the primary identifier, and the stroke is removed from the association lines. Unfortunately, Barker ER has no notation for alternate identifiers, so now both external uniqueness constraints are lost.
A third approach is to introduce an ordinal number as part of the identifier. Here the number is used to count the number of times the same employee visited the same country. For example, my first visit to Belgium is distinguished from my second visit to Belgium simply by including "first" and "second" in the definite descriptions. This visit number is included in the models in Figure 6. For example, the first and second visits of employee 1001 to Belgium and Norway map to the tuples ('1001', 'BE', 1), ('1001', 'BE', 2), ('1001', 'NO', 1), and ('1001', 'NO', 2) respectively.
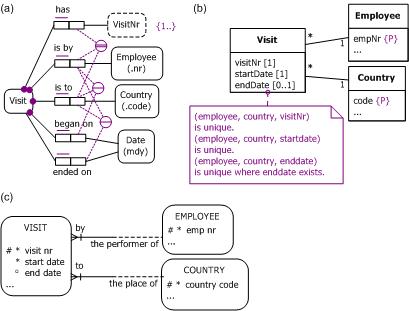
Figure 6. Adding ordinal numbers to help identify visits in (a) ORM, (b) UML, and (c) Barker ER.
Conclusion
This article discussed three ways to maintain a basic history of non-functional, changeable fact types for the common case of a repeatable, many:many fact type:
- include a distinguishing temporal role as part of the identifier;
- introduce a simple, visible identifier;
- introduce an ordinal number as part of the identifier.
While this covers the most common data model pattern in this category, in practice other complexities can arise that require further analysis. We examine some of these tricky cases in the next article.
References
[1] R. Barker. CASE*Method: Tasks and Deliverables. Addison-Wesley: Wokingham, England (1990). ![]()
[2] P. P. Chen. "The Entity-Relationship Model -- Towards a Unified View of Data," ACM Transactions on Database Systems, Vol. 1, No. 1 (1976), pp. 9-36. ![]()
[3] M. Curland & T. Halpin. "Model Driven Development with NORMA," Proc. 40th Int. Conf. on System Sciences (HICSS-40). IEEE Computer Society (January 2007), 10 pages, CD-ROM. ![]()
[4] T.A. Halpin. Information Modeling and Relational Databases. Morgan Kaufmann: San Francisco (2001). ![]()
[5] T.A. Halpin. "ORM 2," On the Move to Meaningful Internet Systems 2005: OTM 2005 Workshops. eds. R. Meersman, Z. Tari, P. Herrero, et al. Springer LNCS 3762: Cyprus (2005), pp. 676-687. ![]()
[6] Terry Halpin, "Temporal Modeling (Part
1)," Business Rules Journal, Vol. 8, No. 2 (Feb. 2007), URL: http://www.BRCommunity.com/a2007/b332.html ![]()
[7] Terry Halpin, "Temporal Modeling (Part
2)," Business Rules Journal, Vol. 8, No. 6 (June 2007), URL: http://www.BRCommunity.com/a2007/b351.html ![]()
[8] NORMA website: http://sourceforge.net/projects/orm ![]()
[9] Object Management Group. UML 2.0 Infrastructure.
Object Management Group (2003). URL: http://www.omg.org/uml ![]()
[10] J. Warmer, A. Kleppe. The Object Constraint Language, 2nd Edition. Addison-Wesley (2003). ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules