Ontological Modeling (Part 4)
This is the fourth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL). OWL is based on description logic. A later series of articles will explore other logic-based languages such as Datalog.
The first article[4] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[5] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[6] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). This fourth article discusses OWL in further detail, focusing on basic features expressed in Manchester syntax.
OWL Syntaxes
From now on, our discussion of OWL relates to OWL 2, the latest version of OWL, which was recommended in October 2009 by the W3C.[11] An overview of OWL 2 and its various sublanguages was presented in the previous article.[6]
Table 1 lists the five concrete syntaxes proposed for expressing an OWL 2 ontology in textual form. RDF/XML is the only syntax that is required to be supported by OWL 2 conformant tools, but it is awkward to read and onerous to write. OWL/XML is also designed for processing by XML tools, so it too is painful to read and write. The Functional Syntax is designed to expose the formal structure of an OWL ontology, and is readable by technical users. For general readability purposes, the Manchester syntax[15] and the Turtle (Terse RDF Triple Language) syntax[1] are far easier for non-technical people to use than the other three syntaxes. The Turtle syntax is a subset of Notation 3 (N3), which was the main syntax used in previous articles to express statements in RDF, RDFS, and OWL. Though popular, Turtle is not a product of the OWL working group. The Manchester syntax is typically a little easier to read than Turtle syntax, and is structured in a way to facilitate specifying a large list of OWL statements in one go.
OWL Syntax |
Status |
Purpose |
RDF/XML |
Required |
Interchange between tools |
OWL/XML |
Optional |
Facilitate processing by XML tools |
Manchester Syntax |
Optional |
Facilitate reading/writing OWL DL ontologies |
Functional Syntax |
Optional |
Expose the formal structure of ontologies |
Turtle |
Optional and unofficial |
Facilitate reading/writing RDF triples |
As a simple example of all five syntaxes, the statements in Table 2 can be used to assert that Obama is a politician (i.e., the individual thing referenced in the current document as Obama is an instance of the class referenced in the current document as Politician) and that each politician is a person (i.e., the Politician class is a subclass of the Person class). Overall, I consider the Manchester Syntax to be the most convenient of the five syntaxes for communicating typical ontologies to non-technical people. So from now on, I'll phrase most of the OWL examples in terms of Manchester syntax.
OWL Syntax |
Statement that |
Statement that |
RDF/XML |
<Politician rdf:about="Obama"/> |
<owl:Class rdf:about="Politician"> |
OWL/XML |
<ClassAssertion>
|
<SubClassOf> |
Manchester |
Individual: Obama |
Class: Politician |
Functional |
ClassAssertion( :Politician :Obama ) |
SubClassOf( :Politician :Person ) |
Turtle |
:Obama rdf:type :Politician . |
:Politician rdfs:subClassOf :Person . |
Manchester Syntax for Previously Discussed Features
This section reviews the features of OWL that were discussed in previous articles, this time presenting the Manchester syntax instead of the N3 syntax used earlier. OWL statements are binary relationships expressed in RDF as (subject, predicate, object) triples. Subjects and predicates are resources, which in OWL 2 are identified using IRIs (Internationalized Resource Identifiers)[2] instead of URIs, to cater for non-English characters. Objects may be resources or literals. For convenience, namespace prefixes may be declared as abbreviations, using a prefix command of the form:
Prefix: namespacePrefix: IRI
This is similar to Turtle, except "Prefix:" is used instead of "@prefix". The prefixes "rdf:", "rdfs:", "owl:", and "xsd:" are predefined. Each user-defined prefix used in an ontology document must have exactly one prefix declaration in the ontology document. Here are two example prefix declarations, one predefined and one user-defined:
Prefix: owl: <http://www.w3.org/2002/07/owl#>
Prefix: gup: <http://www.galacticUni.edu/programs#>
If no prefix is supplied, the current document is assumed to be the namespace. I will make this assumption for the following examples. Literals are delimited by double-quotes (e.g., "64"), and may be typed (e.g., "64"^^xsd:integer).
An individual resource may be declared by prepending "Individual: " to its name, optionally followed by a declaration of properties that apply to it. For example, the classes to which the individual belongs may be listed after "Types: ". An individual may belong to many classes at once. For example:
Individual: Obama
Types: Politician, MalePerson
In Turtle this could be expressed (using "a" for "rdf:type") as
:Obama a :Politician.
:Obama a :MalePerson.
or (using a semicolon to assume the same subject) as
:Obama a :Politician; a :MalePerson.
A class may be declared after "Class: ", and declared as a subclass of some (typically other) class using "SubClassOf". For example:
Class: Politician
SubClassOf: Person
In OWL, subclassing is reflexive (so each class is a subclass of itself) and transitive (so if A is a subclass of B, and B is a subclass of C, then A is a subclass of C). This differs from the subtyping relationship in ORM, which for efficiency reasons is used only for proper subtyping (and hence is irreflexive) that is direct (and hence is intransitive).
In Manchester syntax, a binary fact that relates individuals may be specified by declaring the subject as an individual and then listing the predicate and object of that statement after "Facts: ". One or more facts may be listed using comma separators. For example, we could express the facts that Terry is the husband of Norma and that Terry is the father of Selena as follows:
Individual: Terry
Facts: isHusbandOf Norma, isFatherOf Selena
In Turtle, the same two facts may be expressed as: ":Terry :isHusbandOf :Norma; :isFatherOf :Selena.".
Recall that a domain of a binary predicate is a class to which its subject must belong, and a range of a binary predicate is a class to which its object must belong. In Manchester syntax, a predicate may be declared as an ObjectProperty, and its domain(s) and ranges(s) specified after "Domain: " and "Range: " respectively. For example:
ObjectProperty: isFatherOf
Domain: MalePerson
Range: Person
In Turtle, this could be declared thus:
:isFatherOf rdfs:domain :MalePerson.
:isFatherOf rdfs:range :Person.
A predicate may be assigned multiple domains and ranges, in which case the subject must belong to the intersection of the predicate's domains and the object must belong to the intersection of the predicate's ranges.
As discussed in the previous article,[6] the rdfs:subPropertyOf predicate may be used to declare that all (subject, object) instances of one predicate must be instances of another. In Manchester syntax, this predicate subsetting is declared using the SubPropertyOf predicate. For example:
ObjectProperty: isFatherOf
SubPropertyOf: isaParentOf
In Turtle, this may be expressed thus: ":isFatherOf rdfs:subPropertyOf :isaParentOf.". Note that in Manchester syntax, once a resource is declared you can immediately list all of its properties in one go without having to repeatedly declare the resource in order to list each property one at a time. For example, you could declare the fatherhood predicate along with its superproperty, domain, and range together thus:
ObjectProperty: isFatherOf
SubPropertyOf: isaParentOf
Domain: MalePerson
Range: Person
The second article in this series[5] discussed the use of blank nodes in N3 to deal with cases that would be formalized in logic using existential quantifiers. For example, suppose we want to assert that Obama is a father of some person. In predicate logic, using the individual constant o for Obama, we could express this as follows: ∃x(Person x & o isFatherOf x). You can read this as: There exists something (let's call it x), such that x is a person, and Obama is father of x. In both N3 and Turtle, an expression of the form a R [ S b ], where a and b are individuals and R and S are predicates, may be read as a R's something that S's b. Hence the following Turtle expression states that Obama is a father of some person:
:Obama :isFatherOf [ a :Person].
i.e., Obama is father of something that is a person. This blank node notation is awkward, and becomes even harder to understand once you use it to define derived predicates (as we'll see in a later article). Happily, the Manchester syntax allows you to use "some" for the existential quantifier. So we can state that Obama is father of somebody simply as follows:
Obama isFatherOf some Person
I think you'll agree that this is much easier to read than the blank node formulation. With more complex examples, the Manchester syntax is often much more intuitive than the other syntaxes. I'll be covering many such cases later, but if you want some quick evidence in support of this readability claim, look at the comparative examples in the W3C's primer on OWL 2.[12]
The previous article briefly discussed cardinality restrictions using RDF/XML syntax, but those need to be understood as local restrictions applying only to the class being defined rather than as global restrictions on the underlying predicate. Because this is radically different from the way in which related constraints in information modeling approaches such as ORM, ER, and UML are interpreted, I'll postpone a detailed discussion of them until the next article. For now, we'll look instead at how OWL deals with some notions that are commonly found in information modeling approaches.
Comparing Individuals and Comparing Classes
Recall that OWL predicates are directed, binary relationship types that map subject individuals (instances) to object individuals. OWL includes a predefined, universal class called owl:Thing that includes all individuals. It also predefines the empty class owl:Nothing, which has no members. By default, all OWL predicates have an unrestricted domain and range (equal to owl:Thing).
In mathematics and logic, the identity relationship is usually denoted by "=" and read as "equals". Similarly, the non-identity relationship is usually denoted by "≠" and is read as "is not equal to". In mathematics and logic, these two operators can be used between any compatible expressions (e.g., 2 = 1+1, {1, 2} = {2, 1}).
OWL predefines the owl:sameAs and owl:differentFrom predicates for "=" and "≠" respectively, when they apply between individuals (so their range and domain is owl:Thing). These predicates are used to declare whether two IRIs refer to the same individual or to different individuals. This is quite useful for relating individuals that may be named differently in different documents, but can also be used to equate or distinguish individuals in the same document.
OWL predefines the owl:equivalentClass predicate for equating two classes or class expressions. In Manchester syntax, this is called "EquivalentTo". OWL does not define a single predicate for expressing non-identity between classes, but this can be expressed using negation (see later article). However, OWL DL (but not OWL Lite) includes the owl:disjointWith predicate to indicate that the extensions of two class descriptions are mutually exclusive (i.e., they have no individuals in common). In Manchester syntax, "DisjointClasses: " is prepended before the two class descriptions. Table 3 shows some simple examples of these kinds of comparisons in both Manchester and Turtle syntax.
Manchester syntax |
Turtle Syntax |
Individual: Elvis |
:Elvis owl:sameAs :TheKing. |
Class: Person |
:Person owl:equivalentClass :Human. |
DisjointClasses: Man, Woman |
:Man owl:disjointWith :Woman. |
Functional, Inverse, and Key Relationships
By default, all OWL predicates are optional and many-to-many (m:n). Although the predefined predicates for equating and distinguishing individuals have unrestricted domains and ranges, user-defined predicates typically do have at least one domain and at least one range explicitly declared, and this is always the case for relationship types declared in information modeling approaches such as ORM, ER, and UML.
Figure 1 depicts two associations in (a) ORM and (b) augmented UML notation. Read from left-to-right, the fact type Politician was born in Country is a many-to-one (n:1) association (here each politician was born in at most one country, but many politicians may be born in the same country). In ORM, a predicate reading (in this case "was born in") must be supplied. In UML role names are used, and association names are typically rarely used. The birth role played by instances of Politician is functional (birth country in this association is a function of politician). This is shown in ORM by the uniqueness constraint on the birth role (depicted as a bar over the role), and in UML by a maximum multiplicity of 1 at the country end of the association.
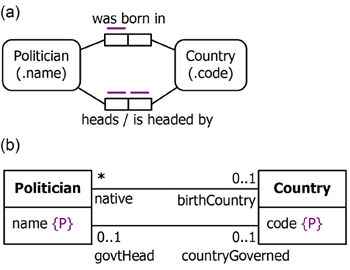
Figure 1. n:1 and 1:1 associations in (a) ORM and (b) UML.
In the real world, each politician must be born in a country. However, in this example, we allow that our information may be incomplete, so that we might not know the birth country of some politicians in our model. For this reason, the birth role has been left optional (as shown by the absence of mandatory role dot on the birth role in ORM, and declaration of a minimum multiplicity of 0 on the birthCountry role in UML).
The fact type Politician heads Country is one-to-one (1:1), because each politician heads at most one country and each country is headed by at most one politician. This is shown in ORM by a uniqueness constraint on each of the two roles, and in UML by a maximum multiplicity of 1 at each association end. Figure 2 depicts these two cases using an instance diagram to populate a binary predicate R.
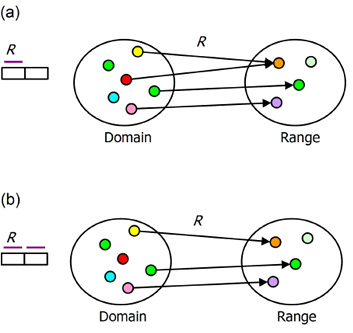
Figure 2. (a) The predicate R is n:1. (b) The predicate R is 1:1.
Recall that OWL confusingly uses the term "property" to mean predicate. Hence an n:1 predicate is called a functional property. In Manchester syntax, a functional predicate is declared as an object property, and then its functional nature is declared by including Functional as one of its characteristics. In Turtle, the predicate is classified to be of type owl:FunctionalProperty.
ORM treats an elementary fact type as a set of one or more typed predicates. In Figure 1(a). the head of government fact type has a forward predicate reading (heads) as well as an inverse predicate reading (is headed by) directed from Country to Politician (a slash "/" separates forward and inverse readings). OWL allows you to declare one predicate to be the inverse of another using the owl:inverseOf predicate. In Manchester syntax, you prepend "InverseOf: " to the inverse predicate.
OWL 2 allows you declare an identification scheme for each instance of a class by declaring a collection of one or more key predicates (cf. the relational data model notion of a primary key), using the owl:hasKey predicate. For example, in Figure 1 politicians are identified by their name and countries by their country codes. Here the ORM diagram depicts this compactly using parenthesized reference modes, but internally these are expanded to the injective reference relationships Politician has PoliticianName and Country has CountryCode. UML has no graphic notation to depict unique attributes, much less primary keys, so I have augmented UML here with the {P} annotation for that purpose. In Manchester syntax, you prepend "HasKey: " to the key predicate(s). Table 4 provides examples of Manchester and Turtle syntax for the OWL 2 features discussed in this section, based on the model in Figure 1.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: wasBornIn |
:wasBornIn a owl:FunctionalProperty. |
ObjectProperty: heads |
:heads a owl:FunctionalProperty. |
Class: Politician |
:Politician owl:hasKey ( :hasName ) . |
Knowledge of functional properties enables OWL tools to make useful inferences. For example, given the following
Individual: Terry
Facts: wasBornIn TheLuckyCountry, wasBornIn Australia
we may deduce
TheLuckyCountry SameAs Australia.
As another example based on different spellings being allowed for the name of the Goddess of the Earth in Greek mythology, given the following
ObjectProperty: isMotherOf
Characteristics: InverseFunctional
Individual: Gaia
Facts: isMotherOf Chronos
Individual: Gaea
Facts: isMotherOf Chronos
we may deduce
Gaia SameAs Gaea.
Functional and inverse functional declarations apply globally to the predicate in all its contexts. OWL cardinality constraints, however, apply only locally to the domain classes being introduced in a local context. This local nature of cardinality restrictions differs markedly from the usual approach in information modeling, and I'll have more to say about this in the next article.
Conclusion
This article introduced the Manchester syntax for OWL 2, reviewed previously-discussed OWL features using this new syntax, and covered some further features of OWL, including comparison operators, functional predicates, and inverse functional predicates. The next article examines further features of OWL 2, and discusses some major differences between OWL and popular information modeling approaches.
References
[1] D. Beckett & T. Berners-Lee. Turtle – Terse RDF Triple Language. W3C (2008). URL: http://www.w3.org/TeamSubmission/turtle/#sec-diff-n3 ![]()
[2] M. Duerst & M. Suignard. RFC 3987: Internationalized Resource Identifiers (IRIs). IETF, (January 2005). URL: http://www.ietf.org/rfc/rfc3987.txt ![]()
[3] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition. Morgan Kaufmann: San Francisco (2008).
[4] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html ![]()
[5] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html [Erratum: In the original version of the second article in this series, the discussion of transitivity of subclassing incorrectly used "a" instead of "rdfs:subClassOf" in the inference example for MaleSinger, Singer, and Person.] ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[7] W3C. RDF Vocabulary Description Language 1.0: RDF Schema, (2004). URL: http://www.w3.org/TR/rdf-schema/
[8] W3C. OWL Web Ontology Language Overview. W3C (2004). URL: http://www.w3.org/TR/2004/REC-owl-features-20040210/
[9] W3C. Notation 3 (N3): A Readable RDF Syntax, ed. T. Berners-Lee, (2006). URL: http://www.w3.org/DesignIssues/Notation3
[10] W3C. OWL 2 Web Ontology Language: New Features and Rationale. W3C (2009). URL: http://www.w3.org/TR/owl2-new-features/
[11] W3C. OWL 2 Web Ontology Language: Document Overview. W3C (2009). URL: http://www.w3.org/TR/owl2-overview/ ![]()
[12] W3C. OWL 2 Web Ontology Language: Primer. W3C (2009). URL: http://www.w3.org/TR/owl2-primer/ ![]()
[13] W3C. OWL 2 Web Ontology Language: Profiles. W3C (2009). URL: http://www.w3.org/TR/owl2-profiles/
[14] W3C. OWL 2 Web Ontology Language: Quick Reference Guide. W3C (2009). URL: http://www.w3.org/TR/owl2-quick-reference/
[15] W3C. OWL Web Ontology Language Manchester Syntax . W3C (2009). URL: http://www.w3.org/TR/owl2-manchester-syntax/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules