Ontological Modeling (Part 5)
This is the fifth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL). OWL is based on description logic. A later series of articles will explore other logic-based languages such as datalog.
The first article[3] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[4] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[5] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[6] discussed basic features of OWL, mainly using Manchester syntax. The current article explores OWL in more depth.
Some OWL Taxonomy
From now on, we use the term "OWL" by default for version 2 of OWL (OWL 2). Figure 1 shows a class diagram in the Unified Modeling Language (UML) notation for several concepts in OWL. This diagram is based on a figure in one of the many World Wide Web Consortium (W3C) documents on OWL.[10] Many of the terms in the figure have been discussed briefly in earlier articles. What we called "resources" in our discussion of RDF are now called "entities" in OWL. OWL entities may be named individuals, classes, properties (binary predicates), or data types. This differs somewhat from the use of the term "entity" in Object-Role Modeling (ORM)[2] and Entity Relationship modeling (ER), where all entities are non-lexical individuals (not types or classes).
In OWL, entities are identified by Internationalized Resource Identifiers (IRIs),[1] but unlike some approaches, OWL does not adopt the Unique Name Assumption (UNA). So in OWL the same entity may be assigned different IRIs, even within the same document. Hence the multiplicity constraint of 1 on entityIRI in Figure 1 should instead be 1..* (1 or more). As discussed earlier,[6] OWL includes the SameAs predicate to indicate when two different IRIs denote the same entity (e.g., DownUnder SameAs Australia).
Literals (data values such as names or numerals) are not treated as individuals. This practice differs from formal logic, where literals do count as individuals. Only OWL individuals (not literals) may be members of OWL classes. Recall that owl:Thing is predefined as the class of all individuals, and owl:Nothing is the empty class. In description logic, owl:Thing and owl:Nothing are called the top concept and bottom concept respectively.
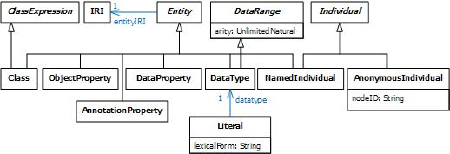
Figure 1.
A UML class diagram of some basic OWL concepts, based on [10]. 
Object properties are binary predicates that relate entities to entities. Data properties are binary predicates that relate entities to literals. Here are some simple examples in Manchester Syntax:
ObjectProperty: wasBornIn
DataProperty: hasName
Individual: Einstein
Facts: wasBornIn Germany, hasName "Albert Einstein"^^xsd:string
The following extreme OWL predicates ("properties") are predefined. The owl:topObjectProperty is the class of all object properties, and hence is a binary predicate relating all individuals in the model to all individuals in the model (its population is the Cartesian product Thing ´ Thing). Every object property is a subproperty of this property. The owl:topDataProperty is the class of all data properties, and hence is a binary predicate relating all individuals to all literals. Every data property is a subproperty of this property. The owl:bottomObjectProperty is the empty object property, and hence is a subproperty of every object property. The owl:bottomDataProperty is the empty data property, and hence is a subproperty of every data property.
Annotation properties are binary predicates that provide informal documentation annotations about ontologies, statements, or IRIs. For instance, the rdfs:comment annotation property is used to provide a comment. Table 1 shows a simple example.
|
Manchester Syntax |
Turtle Syntax |
|
Class: Moon Annotations: rdfs:comment "Natural satellite of a planet or other celestial body." |
:Moon rdfs:comment "Natural satellite of a planet or other celestial body.". |
Other predefined annotation properties are shown below:
- The rdfs:label annotation property is used to provide a human-readable label.
- The rdfs:seeAlso annotation property is used to provide an IRI with another IRI such that the latter provides additional information about the former.
- The rdfs:isDefinedBy annotation property is used to provide an IRI with another IRI where the latter provides a definition of the former.
- An annotation with the owl:deprecated annotation property and the value equal to "true"^^xsd:boolean is used to specify that an IRI is deprecated.
- The owl:versionInfo annotation property is used to provide an IRI with a string that describes the IRI's version.
- The owl:priorVersion annotation property specifies the IRI of a prior version of the containing ontology.
- The owl:backwardCompatibleWith annotation property specifies the IRI of a prior version of the containing ontology that is compatible with the current version of the containing ontology.
- The owl:incompatibleWith annotation property specifies the IRI of a prior version of the containing ontology that is incompatible with the current version of the containing ontology.
OWL tools typically support ontology parsing — the process of converting an ontology document written in a particular syntax into an OWL ontology. Depending on the syntax used, the ontology parser may need to know which IRIs are used for which kinds of entity (e.g., is a predicate an object property, data property, or annotation property?). For example, is wasBornIn an object property or a data property? This typing information can be extracted from declarations — axioms that associate IRIs with entity types (e.g., ObjectProperty: wasBornIn).
Comparing Classes or Datatypes
The previous article[6] discussed the use of the EquivalentTo predicate (Manchester syntax) or owl:equivalentClass predicate (Turtle syntax) for declaring equivalence between two classes or class expressions. In Manchester syntax. "EquivalentTo" may also be used to define a data range. For example, the datatype RatingNr may be confined to {1..7} thus:
Datatype: RatingNr
EquivalentTo: integer[>=1, <=7]
Turtle still uses owl:equivalentClass in combination with restrictions for this task, even though classes and data types are considered disjoint. When the values in the data range comprise a small finite list (as in the above case) the data range may also be specified using an enumerated type (see later article).
The previous article[6] discussed the use of the DisjointWith predicate (Manchester syntax) or owl:disjointWith predicate (Turtle syntax) for declaring that two classes (or class expressions) are disjoint (i.e., mutually exclusive). The class DisjointClasses (Manchester syntax) or owl:AllDisjointClasses (Turtle syntax) is predefined to be a class whose members are pairwise exclusive (i.e., each pair of member classes are disjoint). This provides an efficient way to declare that many classes are pairwise disjoint.
In ORM, top-level entity types are assumed to be mutually exclusive. For example, in the ORM schema in Figure 2(a), if Person, Car, and Dog are not subtypes, then they are assumed to be disjoint. In OWL, however, this disjointness needs to be explicitly stated, as shown in the first statement of Figure 2(b). Here the domain and range specifications restrict the predicates to the object types indicated.

Figure 2 . Declaring some fact types in (a) ORM and (b) OWL (using Manchester syntax).
The single statement using DisjointClasses is equivalent to the lengthier approach of using DisjointWith to declare disjointness between each pair, which in Manchester syntax may be formulated as:
Class: Person
DisjointWith: Car, Dog
Class: Car
DisjointWith: Dog
When using owl:AllDisjointClasses predicate in Turtle syntax, a blank node "[]" (read as "something") is typically used as the subject and the owl:members predicate is typically used to list members. For our current example, this leads to the following Turtle formulation:
[ ] a owl:AllDisjointClasses ;
owl:members ( :Person :Car :Dog ).
Disjoint classes have no individual in common. Recall that the DifferentFrom predicate is used to declare inequality between individuals.[6] Hence, given the following statements (in Manchester syntax)
Individual: Adam
Types: Man
Individual: Eve
Types: Woman
DisjointClasses: Man, Woman
we may infer
Individual: Adam
DifferentFrom: Eve
Comparing Predicates
Previous articles discussed the use of the rdfs:SubPropertyOf predicate for declaring that all (subject, object) instances of one predicate must be instances of another predicate. In Manchester syntax, this predicate subsetting is declared with the SubPropertyOf predicate, e.g.,
ObjectProperty: isFatherOf
SubPropertyOf: isaParentOf
If two predicates must always have the same instance populations, they are said to be (materially) equivalent. This is the same as declaring a subPropertyOf relationship in both directions. In Manchester syntax, equivalence between predicates is declared by listing the predicates after the EquivalentProperties header. In Turtle, the generic owl:equivalentProperty predicate may be used. (If the predicates haven't already been declared as object or data properties, it's better to use the more specific owl:equivalentObjectProperty or owl:equivalentDataProperty.)
Table 2 shows some examples. The first example might be used to assert the constraint that people drive a car if and only if they own the car (this constraint does actually apply in some taxi companies). In ORM, this could be expressed as a pair-equality constraint between the predicates, but it would be more efficient to simply collapse the predicate into one (ownsAndDrives). The second example could be used to support synonyms for predicate readings in the same document (or different documents). A third use of equivalent properties is to specify derivation rules for derived predicates.
Manchester Syntax |
Turtle Syntax |
EquivalentProperties: owns, drives |
:owns owl:equivalentProperty :drives. |
EquivalentProperties: worksFor, isEmployedBy |
:worksFor owl:equivalentProperty :isEmployedBy. |
The DisjointWith predicate (Manchester syntax) or owl:propertyDisjointWith predicate (Turtle syntax) may be used to indicate that the populations of binary predicates must be mutually exclusive. This is equivalent to a pair-exclusion constraint in ORM. For example, in Figure 3 the circled "X" connected to the two predicates graphically depicts the exclusion constraint that no person authored and reviewed the same book. This constraint may be declared in Manchester and Turtle syntax as shown in Table 3.
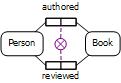
Figure 3. A pair-exclusion constraint in ORM to ensure that nobody reviews a book that he/she authored.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: authored |
:authored rdfs:domain :Person.
|
If more than two predicates are mutually exclusive, it's more efficient in Manchester syntax to simply list them after the DisjointProperties header, e.g.,
ObjectProperty: gotFirstPlaceIn
ObjectProperty: gotSecondPlaceIn
ObjectProperty: gotThirdPlaceIn
DisjointProperties: gotFirstPlaceIn, gotSecondPlaceIn, gotThirdPlaceIn
More about Inverses, Functional Roles, and Keys
The previous article[6] introduced the notions of inverse predicates, functional and inverse functional characteristics, and HasKey predicates in OWL. We now discuss these in more depth. In logic, a binary predicate R is the inverse of a binary predicate S if and only if, given any individuals x and y, xRy if and only if ySx. For example, isaChildOf is the inverse of isaParentOf. In ORM, a slash "/" is used to separate forward and inverse predicate readings (as in Figure 4).
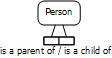
Figure 4. An ORM fact type with forward and inverse predicate readings.
An object property (or object property expression) in OWL may be declared to be the inverse of another other object property (or object property expression) by prepending "InverseOf: " to the inverse predicate (Manchester syntax) or using the owl:inverseOf predicate (Turtle syntax). For example, the forward and inverse predicates in Figure 4 may be declared in OWL as shown in Table 4.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: isaChildOf
|
:isaChildOf owl:inverseOf :isaParentOf. |
OWL does not allow an inverse to be declared for a data property, partly because it never allows a literal to be the subject of a predicate. This is an unfortunate restriction, because we may wish to talk about literals. Consider, for example, the ORM model in Figure 5. OWL lets us declare the data property misspelt, but not its inverse wasMisspeltBy. Moreover, OWL does not let us assert the synonym fact at all. To work around such problems in OWL, you have to cheat, for example by treating Word as an entity type rather than as a value type (literal type).

Figure 5. In ORM, a literal may appear as the subject of a predicate.
By default, all OWL predicates are optional and many-to-many (m:n). To add a uniqueness constraint to the subject role of a binary predicate (object property or data property), declare the predicate to be functional, so that the object is a function of the subject (i.e., for each subject there is at most one object).

Figure 6. Four ORM fact types involving functional predicates.
Figure 6 depicts four ORM fact types involving functional (in this case, n:1) predicates. In information modeling approaches such as ORM, ER, and UML, the two wasBornIn predicates would be treated as different predicates/relationships/associations. However, in OWL we may treat these instead as different occurrences of the same predicate, simply by assigning them the same IRI. A similar situation applies for the two hasName predicate occurrences. (In ER and UML, these predicates would typically be modeled instead as attributes.)
In OWL, if you declare a predicate to be functional, this applies globally to all occurrences of the predicate in the model. For example, the declarations in Table 5 assert that the subject roles of wasBornIn and hasName are functional in every fact type in which they occur (e.g., the fact types in Figure 6 as well as any other fact types involving these predicates).
Manchester Syntax |
Turtle Syntax |
ObjectProperty: wasBornIn
|
:wasBornIn a owl:ObjectProperty,
|
DataProperty: hasName
|
:hasName a owl:DatatypeProperty,
|
If a predicate is an object property, you can add a uniqueness constraint to its object role by declaring the predicate as an inverse functional property. In Manchester syntax, include InverseFunctional as a characteristic of the predicate. In Turtle, declare the predicate as an instance of owl:InverseFunctionalProperty. Inverse functional declarations apply globally to all occurrences of the predicate. For example, the two manages predicates in the ORM model in Figure 7 may be treated as two occurrences of the same predicate in OWL by assigning them the same IRI. The inverse functional nature of the predicate may then be declared as shown in Table 6.
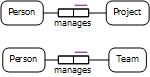
Figure 7. Two ORM fact types involving inverse functional predicates.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: manages |
:manages a owl:ObjectProperty,
|
OWL does not allow a data property to be declared inverse functional. This restriction is again unfortunate, but is consistent with OWL's forbidding of inverses of data properties. In practice, many data properties are either 1:1 or 1:n, thus requiring a uniqueness constraint on the role played by the literal. Although we can't declare uniqueness constraints on roles played by literals as inverse functional characteristics, we can specify such constraints using HasKey declarations.
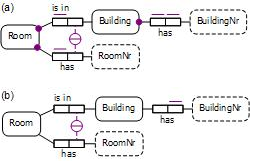
Figure 8. Two ORM fact types involving inverse functional predicates.
The HasKey feature, introduced in OWL 2, partly addresses the need to specify identification schemes (simple or compound) for entity types. For example, consider the ORM schema in Figure 8(a). Here each building is identified by its building number, and each room is identified by combining its local room number with its building. The large dots depict mandatory role constraints (each building has a building number, and each room is in a building and has a room number). Each bar over a role depicts a simple uniqueness constraint, and the circled bar depicts an external uniqueness constraint.
In OWL, the hasBuildingNr predicate would be treated as a key predicate for Building, and the isInBuilding and hasRoomNr predicates would collectively be treated as key predicates for Room. This may be specified as shown in Table 7.
Manchester Syntax |
Turtle Syntax |
Class: Building
|
:Building owl:hasKey ( :hasBuildingNr ).
|
The OWL 2 Primer[7] includes the following claim about keys (my bolding):
"In OWL 2 a collection of (data or object) properties can be assigned as a key to a class expression. This means that each named instance of the class expression is uniquely identified by the set of values which these properties attain in relation to the instance."
A literal reading of this claim suggests that key declarations in OWL provide full identification schemes for entity types, which would entail all the mandatory role and uniqueness constraints shown in Figure 8.
However, the formalization in the OWL 2 direct semantics document[8] indicates that declaring one or more key properties for a class expression simply asserts that each related object set relates to at most one subject. This entails that in this example, only the right-hand uniqueness constraints are captured by the key declarations, as shown in Figure 8(b). In that case, further declarations would be needed to capture the left-hand uniqueness constraints (e.g., by declaring the predicates to be functional) and mandatory role constraints (see next article). With this interpretation, OWL keys capture only part of the notion of keys in database modeling. Given that the direct semantics document provides a formalization, it's safer to assume that the direct semantics document is correct in this regard and hence that the above claim from the primer is misleading.
Conclusion
This article covered further aspects of OWL 2, discussing terminology (e.g., object, data, and annotation properties), comparison operators on classes, datatypes, and predicates, and then explored inverses, functional characteristics and HasKey predicates in more depth.
Functional and inverse functional declarations apply globally to the predicate in all its contexts. In contrast, OWL cardinality constraints apply only locally to the domain classes being introduced in a local context. This local nature of cardinality restrictions differs markedly from the usual approach in information modeling. Another major difference between OWL and data modeling approaches is that OWL schemas do not constrain fact populations to conform in the way that database models do. For example, if you assert that each parent has at least one child, and that Obama is a parent, no check will be made to ensure that some named individual is declared as a child of Obama. I'll have more to say about such differences in following articles, as well as discussing further features of OWL 2.
References
[1] M. Duerst & M. Suignard. RFC 3987: Internationalized Resource Identifiers (IRIs). IETF, (January 2005). URL: http://www.ietf.org/rfc/rfc3987.txt ![]()
[2] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[3] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html ![]()
[4] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html ![]()
[5] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[7] W3C. OWL 2 Web Ontology Language: Primer. W3C (2009). URL: http://www.w3.org/TR/owl2-primer/ ![]()
[8] W3C. OWL 2 Web Ontology Language: Direct Semantics . W3C (2009). URL: http://www.w3.org/TR/owl2-direct-semantics/ ![]()
[9] W3C. OWL Web Ontology Language Manchester Syntax . W3C (2009). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[10] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax . W3C (2009). URL: http://www.w3.org/TR/owl2-syntax/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules