This is the sixth in a series of articles on ontology-based approaches to modeling.  The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL).  OWL is based on description logic.  A later series of articles will explore other logic-based languages such as datalog.

The first article^[2] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches.  The second article^[3] discussed the N3 notation for RDF, and covered the basics of RDF Schema.  The third article^[4] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL).  The fourth article^[5] discussed basic features of OWL, mainly using Manchester Syntax.  The fifth article^[6] discussed OWL taxonomy, comparison operators for classes, data types and predicates, and examined inverses, functional roles and keys in more depth.  The current article provides a detailed coverage of cardinality restrictions in OWL 2.

Unqualified Cardinality Restrictions in OWL 2

An earlier article^[4] provided basic coverage of cardinality restrictions in OWL 1.  We now provide a deeper coverage of cardinality restrictions, as defined in OWL 2.^[7]  Unless otherwise indicated, we henceforth use "OWL" to mean "OWL 2."  OWL statement triples are the form (subject, predicate, object).  OWL properties are binary predicates that map instances of a class (called the domain of the relation) to instances of a class or datatype (called the range of the relation).  By default, OWL properties are many-to-many (m:n) relationships with each role optional for its type.  Figure 1 provides an abstract example of this situation.

Declaring a predicate to be functional adds a uniqueness constraint to its first role (so each subject instance relates to at most one object).  Declaring an object property (entity to entity relationship) to be inverse functional adds a uniqueness constraint to its second role (so each object relates to at most one subject).  Data properties (entity-to-literal relationships) cannot be declared to be inverse functional.

Roughly speaking, cardinality restrictions in OWL provide one way to specify constraints that in the Unified Modeling Language (UML) are known as multiplicity constraints and in Object-Role Modeling (ORM)^[1] involve mandatory role constraints, uniqueness constraints, and/or frequency constraints.  As we'll see, cardinality restrictions go further by allowing you to apply these constraints to specific domains (e.g., subclasses or even individuals) and specific ranges.  This differs from functional and inverse functional declarations, which always apply globally to the predicate in all its contexts.^[6]

The class owl:Thing is the class of all individuals, and is said to be unrestricted.  A class expression may be specified as a named or an unnamed subclass of owl:Thing by declaring it to be a restriction (an instance of the class owl:Restriction) obtained by applying some condition (e.g., a cardinality constraint) to a predicate (object of the owl:onProperty predicate).

For a given predicate R with domain A and range B, minCardinality is the minimum number of instances of B to which each population instance of the subject class A relates via R (cf. minMultiplicity in UML).  To declare the first role of R to be mandatory for the subject class A, you can assign a minimum cardinality of 1 (at least).  We now illustrate this with an example.

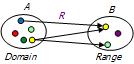
Figure 1.  The predicate R maps instances of domain A to instances of range B.  Here, R is m:n with roles optional.

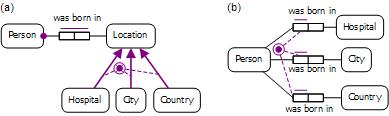
Figure 2.  Some different options in ORM for constraining persons to be born somewhere.

Figure 2(a) is an ORM schema with the fact type Person was born in Location, with Location partitioned into three subtypes.  For simplicity, reference schemes are omitted.  The large dot attached to Person's role in the birth fact type depicts a mandatory role constraint, which verbalizes as:  Each Person was born in some Location.  In this model, we must know at least one birth location (possibly two or three, depending partly on how complete our knowledge is) for each person.  The bar over the birth predicate depicts a spanning uniqueness constraint, indicating that the fact type is m:n and that its fact entries are unique.

Figure 2(b) shows an alternative ORM schema, with three fact types:  Person was born in Hospital; Person was born in City; Person was born in Country.  The circled dot is an inclusive-or constraint (also known as a disjunctive mandatory role constraint), which may be verbalized as:  Each Person was born in some Hospital or some City or some Country.  The bars over the roles played by Person denote uniqueness constraints:  Each Person was born in at most one Hospital; Each Person was born in at most one City; Each Person was born in at most one Country.  In ORM there is no way to graphically add these uniqueness constraints to Figure 2(a), unless we first derive the fact types in Figure 2(b), and assert the uniqueness constraints on those derived fact types.  Although the constraints could be added to model (a) as textual constraints in FORML, many ORM modelers would prefer model (b), as it captures all the constraints visually and has a more efficient relational mapping.

In ORM, the three "was born in" predicates in Figure 2(b) are considered to be distinct.  In OWL, however, we may treat these as the same predicate by assigning them the same Internationalized Resource Identifier (IRI).  If we do this, and no other occurrences of "was born in" exist in the model, then in OWL we could define the range of the wasBornIn predicate to be Hospital or City or Country (the union of the three).

In OWL, we could even allow the range of the wasBornIn predicate to be owl:Thing, as shown in Figure 3.  Here we have made it mandatory to know some birthplace for people but we have made it optional to know this for animals.  Again, OWL allows us to treat both occurrences of wasBornIn as the same predicate.  Regardless of which of Figure 2(a), Figure 2(b), or Figure 3 we use for the model, we may declare Person's mandatory birthplace constraint in OWL by declaring Person to be a subclass of those things that play the subject role of the wasBornIn predicate with a minCardinality of 1 (or more).  Table 1 shows how to declare this in Manchester Syntax and Turtle Syntax, choosing a minimum cardinality of 1.

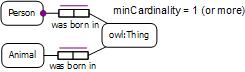
Figure 3.  Restricting Person to be a subclass of things that were born somewhere.

For a given predicate R, with domain A and range B, maxCardinality is the maximum number of instances of B to which each population instance of the subject class A relates via R (cf. maxMutiplicity in UML).  For example, to declare a uniqueness constraint on the first role of R for a given subject class, assign a maximum cardinality of 1.  As a shortcut, if minCardinality = maxCardinality, you can set both at once using exactCardinality.  For example, Table 2 shows the Manchester Syntax and Turtle Syntax for declaring that each person was born in at most one thing, and that each person was born in exactly one thing.  As discussed in the next section, maximum and minimum cardinality restrictions are typically qualified with respect to a specified range.

Qualified Cardinality Restrictions in OWL 2

Qualified Cardinality Restrictions also restrict the range (B) of the predicate R, for the subject class expression A being constrained.  In Manchester Syntax, we include the specific range after the relevant min n, max n, or exactly n cardinality specification.  In Turtle, we use the owl:onClass predicate to declare the range restriction after the owl:minQualifiedCardinality n, owl:maxQualifiedCardinality n, or owl:QualifiedCardinality n specification.  For example, Table 2 shows the Manchester Syntax and Turtle Syntax for declaring that each person was born in at least one country, each person was born in at most one country, and each person was born in exactly one country.

OWL DL and OWL Full (but not OWL Lite) allow restrictions with a minCardinality or minQualifiedCardinality of n > 1.  In ORM this is equivalent to adding the frequency constraint "≥ n" to the mandatory role constraint.  A frequency constraint of "≥ n" (or "≤ n") on a role means that, for each state of the information model, each instance that populates that role must appear at least n (or at most n) times in that role population.  Figure 4 illustrates these equivalences for minimum/maximum qualified cardinalities.

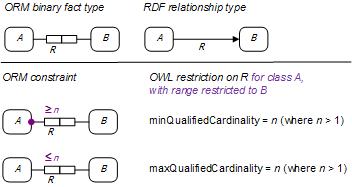
Figure 4.  Equivalent ORM for setting an OWL minQualifiedCardinality restriction = n when  n > 1.

For example, Figure 5(a) shows an ORM model for the m:n fact type Translator speaks Language.  The mandatory role constraint and frequency constraint on the role played by Translator combine to verbalize as follows:  Each Translator speaks at least 2 instances of Language.  In other words, each translator speaks at least two languages.  The UML class diagram in Figure 5(b) captures this by the "2..*" multiplicity constraint on the association role played by Language.  Figure 5(c) shows another ORM example where the maximum number of wives depends on the subject's religion (the OWL restrictions are also included on the diagram).  Table 4 shows how to declare these qualified cardinality restrictions in Manchester and Turtle Syntax.

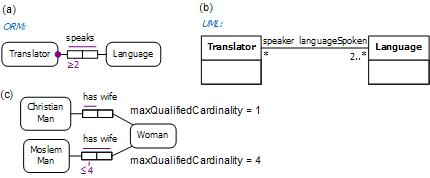
Figure 5.  Examples of minimum and maximum qualified cardinalities above 1.

Figure 6.  A restricted mandatory role constraint (footnote 1) and a restricted uniqueness constraint (footnote 2).

FunctionalProperty and InverseFunctionalProperty declarations are global constraints (as are inverseOf and ring constraints (see later article)), applying to the predicate in all its occurrences (for all its classes).  In contrast, OWL cardinality constraints apply only locally to the specific domain and range currently under consideration.  For example, consider the ORM schema in Figure 6.  In the fact type Employee drives Car, the drives predicate is optional and m:n.  However, the two textual constraints in FORML^{[1, p. 291]} add a restricted mandatory role constraint (shown as constraint footnote 1) and a restricted uniqueness constraint (shown as constraint footnote 2).

Here the drives predicate is functional only with respect to NonExecutive, not Employee.  For this case, we should not declare drives as a FunctionalProperty, because that would then apply to all employees (and any other subjects of the drives predicate in an OWL version of the model).  Both of these restricted constraints should be declared in OWL using qualified cardinality restrictions.  Table 5 shows how to do this using Manchester Syntax and Turtle Syntax.

In practice, it is very rare to encounter explicit declarations for minCardinality = 0 and minQualifiedCardinality = 0 because these apply by default, so may be ignored.  However, setting the maximum cardinality to zero does have some use.  The setting maxCardinality = 0 means that each instance of the subject class expression A is related via the predicate R to no object instance.  The setting maxQualifiedCardinality = 0 means that each instance of the subject class expression A is related via R to no instance of the specified range B.  These restrictions are used mainly in defining subclasses, and the qualified version is typically used in such cases.  Figure 7(a) and Figure 7(a) summarize the corresponding ORM patterns, while Figure 7(c) provides a concrete example.

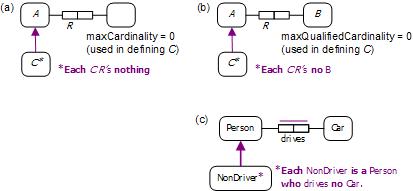
Figure 7.  Using zero-valued maxCardinality and maxQualifiedCardinality restrictions to define subtypes.

Table 6 shows how to express the NonDriver example in Manchester Syntax.  We'll see how to do it in Turtle Syntax in the next article after we have discussed intersections.  We will also see some alternative ways to formulate some of the Manchester Syntax expressions.

Note that individuals may also be declared to be members of class expressions that are defined using cardinality restrictions.  For example, the population of the derived fact type in Figure 8 reveals some facts about two of my favorite authors.  Isaac Asimov wrote 506 books, while J. R. R. Tolkien wrote 23 books.  If the population of the fact type Person authored Book is complete with respect to authors of interest, the derivation rule in Figure 8 may be used to derive the number of books written for each author.  Regardless, we can still assert these facts directly in OWL using the Manchester and Turtle Syntax shown in Table 7.

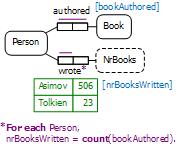
Figure 8. Two ORM fact types involving inverse functional predicates.

Conclusion

The current article provided a detailed coverage of cardinality restrictions (unqualified and qualified) in OWL 2.  The ability in OWL to reuse the same predicate with different subject and object classes/types allows considerable flexibility for defining classes in terms of predicate restrictions for specific domains and ranges.  The next article will explore other features of OWL, such as ring constraints and class-forming operations on classes (e.g., union, intersection, complement).

References

[1]  T.A. Halpin & T. Morgan.  Information Modeling and Relational Databases, 2nd edition.  Morgan Kaufmann:  San Francisco (2008).  

[2]  T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol. 10, No. 9 (Sep. 2009), URL:  http://www.BRCommunity.com/a2009/b496.html  

[3]  T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol. 10, No. 12 (Dec. 2009), URL:  http://www.BRCommunity.com/a2009/b513.html  

[4]  T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol. 11, No. 3 (Mar. 2010), URL:  http://www.BRCommunity.com/a2010/b527.html  

[5]  T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol. 11, No. 6 (Jun. 2010), URL:  http://www.BRCommunity.com/a2010/b539.html  

[6]  T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol. 11, No. 12 (Dec. 2010), URL:  http://www.BRCommunity.com/a2010/b570.html  

[7]  W3C.  OWL 2 Web Ontology Language:  Primer.  W3C (2009).  URL:  http://www.w3.org/TR/owl2-primer/  

[8]  W3C.  OWL 2 Web Ontology Language:  Direct Semantics .  W3C (2009).  URL:  http://www.w3.org/TR/owl2-direct-semantics/  

[9]  W3C.  OWL Web Ontology Language Manchester Syntax .  W3C (2009).  URL:  http://www.w3.org/TR/owl2-manchester-syntax/  

[10]  W3C.  OWL Web Ontology Language Structural Specification and Functional-Style Syntax .  W3C (2009).  URL:  http://www.w3.org/TR/owl2-syntax/  

# # #