Ontological Modeling (Part 9)
This is the ninth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL). OWL is based on description logic. A later series of articles will explore other logic-based languages such as datalog.
The first article[2] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[3] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[4] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[5] discussed basic features of OWL, mainly using Manchester syntax. The fifth article[6] discussed OWL taxonomy, comparison operators for classes, data types and predicates, and examined inverses, functional roles and keys in more depth. The sixth article[7] covered cardinality restrictions in OWL 2. The seventh article[8] discussed the union, intersection, and complement operators in OWL 2. The eighth article[9] explored support for ring constraints within OWL 2. The current article discusses enumerated types as well as value restrictions on properties in OWL 2.
Enumerated Types in OWL 2
Recall that in OWL, entities are identified by Internationalized Resource Identifiers (IRIs), and are grouped into classes (e.g., Person, Book) to indicate their type(s). In contrast, literals (data values such as names or numbers) are grouped into datatypes (e.g., xsd:string, xsd:nonNegativeInteger). An earlier article[8] discussed how to define a new class or datatype by specifying its intension (i.e., meaning) in terms of operations on classes or datatypes that are already declared. A type definition that specifies the necessary and sufficient conditions for an item to be a member of the type is said to be an intensional definition of the type. For example, Table 1 provides intensional definitions for StudentEmployee and PassGradeNr, in both Manchester and Turtle syntax, assuming that the types referenced (Student, Employee, GradeNr, FailGradeNr) have been previously declared.
Manchester Syntax |
Turtle Syntax |
Class: StudentEmployee |
:StudentEmployee a owl:Class; |
Datatype: PassGradeNr |
:PassGradeNr a rdfs:Datatype; |
The set of all possible instances of a type is said to be the extension of the type. If a class or data range is composed of a known, finite set of items, it may be defined by enumerating (i.e., listing) those items. For example, while EvenDigit could be defined intensionally as {x | x is a digit that is divisible by 2} it could also be defined extensionally as a member of {0, 2, 4, 6, 8}. A type that is defined by enumerating its extension is said to be an enumerated type, and its definition is said to be an extensional definition. In Manchester syntax, the usual set notation is used to specify the extension, using braces as set delimiters and commas as element separators. Turtle syntax instead uses parentheses as set delimiters, spaces as element separators, and owl:oneOf for the set membership operator. Table 2 provides some examples in both syntaxes.
Manchester Syntax |
Turtle Syntax |
Class: Weekday |
:Weekday a owl:Class; |
Datatype: EvenDigit |
:EvenDigit a rdfs:Datatype; |
"Value" Restrictions on Predicates
In its treatment of 'value restrictions', OWL uses the term 'value' loosely to mean either an individual entity or a literal. Given this understanding, a named class or (unnamed) class expression may be defined as the subject of a predicate whose range is restricted to include:
- some specific value
- some value from a specified class or data range
- only values from a specified class or data range
We consider these cases in turn. Figure 1 depicts a binary relation R from a set A to a set B, with elements of the domain and range of the relation depicted as colored dots. Each member of the subset C relates via R to at least the value v in B. So C = {x | xRv}. As shown in the depiction, it is possible that an element of C relates not just to v but also some other element of B. However, each element of C must relate at least to v.
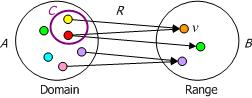
Figure 1. C is restricted to those A domain items that relate via R to at least the value v in the range B.
In Manchester syntax, the set of all elements that relate via R to the value v is expressed simply as "R value v". In Turtle syntax, this is expressed as "[ owl:Restriction; owl:onProperty :R; owl:hasValue :v]". As a simple example, consider the data model in Figure 2, shown in the notations of both Object-Role Modeling (ORM)[1] and the Unified Modeling Language (UML)[10]. Here, MalePerson is a derived subtype, whose instances are restricted to those instances of Person that have male gender. The UML subclass definitions are presented as informal notes.
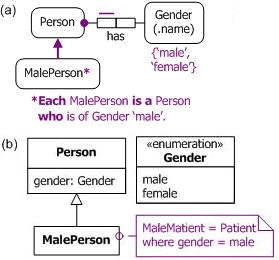
Figure 2. Restricting MalePerson to Person instances that have male gender in (a) ORM and (b) UML.
Treating Gender as an enumerated class of two individuals (male and female), these subtype definitions may be captured in OWL as shown in Table 3. For simplicity, other aspects of the data model are omitted in the OWL code (e.g., the mandatory, functional nature of the hasGender predicate).
Manchester Syntax |
Turtle Syntax |
Class: Gender |
:Gender a owl:Class; |
Class: MalePerson |
:MalePerson a owl:Class; |
Now consider Figure 3, which depicts a binary relation R from a set A to a set B. In this case, each member of the subset C relates via R to some value in D, a subset of B. So C = {x | ∃y(y ∈ D & xRy)}.
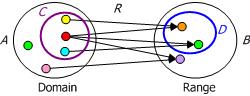
Figure 3. C is restricted to those A domain items that relate via R to some value in the subrange D.
In Manchester syntax, the set of all elements that relate via R to some value in a specified subrange D is expressed simply as "R some D". In Turtle syntax, this is expressed as "[ owl:Restriction; owl:onProperty :R; owl:someValuesFrom :D]". As a simple example, consider the subtyping data model in Figure 4, shown in both ORM and UML notation. Here, Driver is a derived subtype, whose instances are restricted to those instances of Person who drive some vehicle.
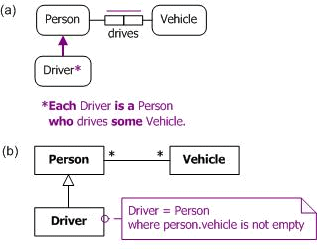
Figure 4. Restricting Driver to Person instances that drive some Vehicle in (a) ORM and (b) UML.
These subtype definitions may be captured in OWL as shown in Table 4. In this case, the subrange Vehicle is the same as the range.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: drives |
:drives rdfs:domain :Person. |
Class: Driver |
:Driver a owl:equivalentClass |
As an example where the subrange is smaller than the range, consider the data model in Figure 5, shown in both ORM and UML notation. Here, CarDriver is a derived subtype, whose instances are restricted to those instances of Person who drive some vehicle that is a car.
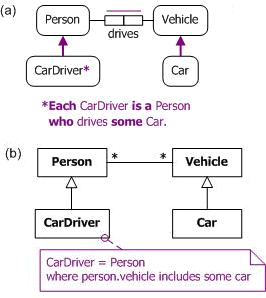
Figure 5. Restricting CarDriver to Person instances that drive some Car in (a) ORM and (b) UML.
Assuming the same object property declarations for the drives predicate, the subtype definitions may be captured in OWL as shown in Table 5.
Manchester Syntax |
Turtle Syntax |
Class: Car |
:Car rdfs:subClassOf :Vehicle. |
Class: Driver |
:Driver owl:equivalentClass |
Now consider Figure 6, which again depicts a binary relation R from a set A to a set B. In this case, each member of the subset C relates via R to some value in the subrange D only. Here we interpret "only" to include in C any domain element that relates via R to no element at all. So the only domain elements excluded from C are those that relate via R to some range element not in D. So C = {x | ∀y(xRy → y ∈ D)}.
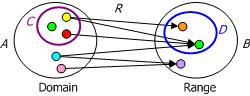
Figure 6. C is restricted to those A domain items that relate via R only to some value in the subrange D (if at all).
As a simple example, consider the data model in Figure 7, shown in both ORM and UML notation. Here, CarOnlyDriver is a derived subtype, whose instances are restricted to those instances of Person who drive only vehicles that are cars. This subtype includes those people who drive no vehicles at all.
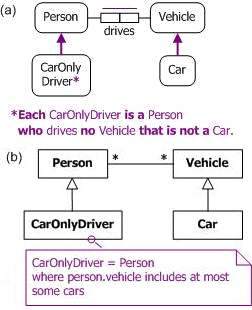
Figure 7. Restricting CarOnlyDriver to Person instances that drive only cars (if at all) in (a) ORM and (b) UML.
In Manchester syntax, the set of all elements that relate via R to some value in a specified subrange D only (if at all) is expressed simply as "R only D". In Turtle syntax, this is expressed as "[ owl:Restriction; owl:onProperty :R; owl:allValuesFrom :D]". Assuming the previous declarations for the drives predicate and Car subclass, the subtype definition for CarOnlyDriver may be captured in OWL as shown in Table 6.
Manchester Syntax |
Turtle Syntax |
Class: CarOnlyDriver |
:CarOnlyDriver owl:equivalentClass |
Conclusion
The current article discussed how to specify enumerated types in OWL, and how to define a subclass by restricting its members to those domain elements of a predicate that relate to: (a) a specific value; (b) some value from a specified (sub)range; or (c) only values from a specified (sub)range. The next article will discuss some advanced features of OWL 2, such as property chains.
References
[1] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[2] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html ![]()
[3] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html ![]()
[4] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[5] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol.
11, No. 12 (Dec. 2010), URL: http://www.BRCommunity.com/a2010/b570.html ![]()
[7] T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol.
12, No. 2 (Feb. 2011), URL: http://www.BRCommunity.com/a2011/b579.html ![]()
[8] T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol.
12, No. 6 (Jun. 2011), URL: http://www.BRCommunity.com/a2011/b602.html ![]()
[9] T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol.
12, No. 9 (Sep. 2011), URL: http://www.BRCommunity.com/a2011/b614.html ![]()
[10] Object Management Group. UML 2.0 Superstructure Specification.
Object Management Group (2003). URL: http://www.omg.org/uml ![]()
[11] Object Management Group. UML OCL 2.0 Specification. Object Management Group (2005). URL: http://www.omg.org/docs/ptc/05-06-06.pdf
[12] W3C. OWL 2 Web Ontology Language: Primer. W3C (2009). URL: http://www.w3.org/TR/owl2-primer/
[13] W3C. OWL 2 Web Ontology Language: Direct Semantics. W3C (2009). URL: http://www.w3.org/TR/owl2-direct-semantics/
[14] W3C. OWL Web Ontology Language Manchester Syntax. W3C (2009). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[15] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax. W3C (2009). URL: http://www.w3.org/TR/owl2-syntax/
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules