This is the eleventh in a series of articles on ontology-based approaches to modeling.  The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL).  OWL is based on description logic.  A later series of articles will explore other logic-based languages such as datalog.

 The first article^[2] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches.  The second article^[3] discussed the N3 notation for RDF, and covered the basics of RDF Schema.  The third article^[4] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL).  The fourth article^[5] discussed basic features of OWL, mainly using Manchester syntax.  The fifth article^[6] discussed OWL taxonomy, comparison operators for classes, data types and predicates, and examined inverses, functional roles and keys in more depth.  The sixth article^[7] covered cardinality restrictions in OWL 2.  The seventh article^[8] discussed the union, intersection, and complement operators in OWL 2.  The eighth article^[9] explored support for ring constraints within OWL 2.  The ninth article^[10] discussed enumerated types as well as value restrictions on properties in OWL 2.  The tenth article^[11] examined OWL 2's support for property chains, and compared this with related concepts in data modeling approaches.  The current article discusses the logical status of structural statements in OWL 2, contrasting this with other data modeling approaches that support both integrity constraints and derivation rules.

Some Differences between OWL Ontologies and Typical Databases

In OWL, a named individual is an entity that is named (identified by) a global Internationalized Resource Identifier (IRI).  OWL also allows unnamed or anonymous individuals (corresponding to blank nodes in RDF), which may be referenced within a given ontology by a local nodeID that starts with an underscore, e.g., _:x or _:p1.  If the same nodeID is used in two different ontologies, it need not denote the same individual in both.  So if _:p1 occurs in ontology A and ontology B, and we import the _:p1 in B into A, then we must replace it in A by a fresh nodeID that is new to A (e.g., _:p2).

NodeIDs allow us to assert the existence of an individual without naming it.  Table 1 provides two simple examples.  The first example asserts the existence of a god, using the nodeID "_:g" to denote this god.  This assertion may be rendered in English as "There is a god".  Using "∃" for the existential quantifier "there exists some", and "God x" for the predication "x is a god", this may be formalized in predicate logic as ∃x God x.  The second example asserts the existence of a woman prime minister of Australia, using the node ID "_:p1" to denote this person.  In English, we could express this as "There is a woman who is prime minister of Australia" without knowing her name (at the time of writing, it is Julia Gillard).  Using "&" for "and", this may be formalized in logic as ∃x (Woman x & x isPrimeMinisterOf Australia).

In relational databases, all individuals of interest are normally identified by simple or compound names, so existential assertions like those above are typically not supported, although we can store specific facts that imply them (e.g., "Yahweh is a god", "Julia Gillard is a woman and prime minister of Australia").

From a logical perspective, IRIs correspond to individual constants rather than names in the usual sense they have in relational databases.  For example, the IRI :Paris might be used in a document to denote the capital city of France, whereas the character string 'Paris' might be used for the name of one or more cities or towns or pet cats, as well as a given name of one or more people (e.g., Paris Hilton), and so on.  As discussed in earlier articles^{[3, 5]} an IRI like :Paris is understood to be implicitly prepended by a namespace prefix that identifies the current document, thus providing a truly global identifier.

To illustrate how OWL's treatment of IRI-based identification schemes differs from the value-based identification schemes used in typical data modeling and relational database approaches, consider the simple data model shown in Figure 1.  Here countries are primarily identified by their country code (e.g., "AU" for Australia, and "DE" for Germany), and also have an identifying country name.  Figure 1(a) displays this in Object-Role Modeling (ORM)^[8] notation, using a parenthesized reference mode for the primary reference scheme and an explicit, mandatory, 1:1 fact type for the country name relationship.  Figure 1(b) displays the example in an extended version of the Barker Entity Relationship (ER) notation,^[8] where I have added "{U1}" to indicate that country names are unique for countries.  The "#" indicates the primary identifier and the "*" indicates a mandatory attribute.  Figure 1(c) displays the example in an extended version of the Unified Modeling Language (UML) notation,^[8] where I have added "{P}" to indicate the preferred reference scheme, and "{U1}" to indicate that country names are also unique.  Figure 1(d) displays a relational database schema for the example, using "PK" for the primary key, "U1" for uniqueness, and a bold font for columns that are not nullable.

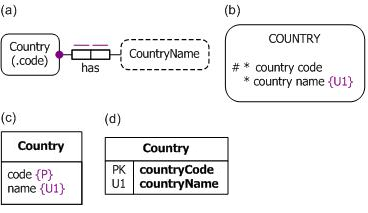
Figure 1.  Identifying countries in (a) ORM, (b) extended Barker ER,
                (c) extended UML, and (d) a relational database.

Table 2 shows one way to code this example in OWL, using techniques discussed in earlier articles.  The data properties are binary relationships that map countries to country code and country name strings.  The subclass restriction for Country declares that each country has exactly one country code and exactly one country name.  The HasKey declarations state that at most one country has any given country code and any given country name.

Notice that OWL has no way to choose one of the hasCountryCode or hasCountryName relationships to be the preferred reference scheme.  So the database distinction between primary and alternate keys is lost.  The OWL code in Table 2 explicitly declares hasCountryCode and hasCountryName as predicates.  Since countries are entities, OWL requires them to be identified by IRIs.  In practice, most OWL users would probably use IRIs such as :Australia and :Germany as IRIs, rather than IRIs such as :AU and :DE.  Although :Australia and :Germany are individual constants rather than name literals, they resemble the names so closely that if we make this choice for IRI we could omit the hasCountryName declarations entirely, thus halving the amount of code used in Table 2.

Regardless of whether we omit the hasCountryName declarations, let us assume that we do use IRIs that resemble country names, and then wish to add just the fact instances shown in Table 3.  Here we have asserted that Australia and Germany are countries, and that Australia has the country code "AU".  Recall that in Table 2 we declared that each country has a country code.  However, in Table 3 we have declared that Germany is a country without explicitly providing a country code for it.  Is this allowed?

If we tried to assert these facts into the relational database shown earlier, we would generate an error because our declaration that each country has a country code is implemented as an integrity constraint, forbidding the countryCode column to include any nulls.  Any attempt to populate the Country table as shown in Table 4 violates this constraint.  This violation would occur regardless of which column is chosen as the primary key.

In contrast, OWL allows the transaction shown in Table 3, because the declaration that each country has a country code is interpreted simply as a proposition, not as a constraint.  Using "∀" for the universal quantifier ("for all") and "→" for "implies", this proposition may be formalized in logic as ∀x(Country x ) → ∃y x hasCountryCode y).  Since we asserted that Germany is a country, the system infers that Germany has a country code, which is currently unknown.  This is allowed in OWL, which adopts open world semantics and permits unnamed individuals.  This marked difference between OWL and typical database approaches is a consequence of its foundation in description logics.  For a readily accessible introduction to description logic (DL), see [12], which also makes the point that "mistaking DL axioms for constraints is a very common source of modeling errors."  The next section explores this issue in more detail.

Propositions, Derivation Rules, and Integrity Constraints

The OWL ontology in Table 5 uses the speaks predicate to relate persons to the languages they speak (if any), and the isFluentIn predicate to relate persons to the languages in which they are fluent (if any).  The subproperty declaration asserts the proposition that each person who is fluent in a language also speaks that language.  In the context of the predicate type declarations, this subproperty declaration may be formalized in logic thus:  ∀x,y (x isFluentIn y → x speaks y).  Hence, from the fact that Terry is fluent in English the system may infer that Terry speaks English. 

Notice that OWL treats the subproperty declaration simply as a conditional proposition.  If we were to model this in a relational database, we have a choice as to how to implement the conditional.  Figure 2(a) shows an ORM schema that implements the conditional as a subset constraint between the two predicates.  With this choice, we must explicitly assert all relevant facts, and the database system will check that each (person, language) pair in the fluency table matches a (person, language) pair in the speaks table.  If we asserted just the two fact instances in Table 5, the subset constraint would be violated because we asserted that Terry is fluent in English without also asserting that Terry speaks English.

Figure 2(b) shows an alternative ORM schema that implements the conditional as a derivation rule on a semiderived fact type indicated by the "+" superscript.  This allows us to assert some speaks facts, and have other speaks facts derived from fluency facts, so the data entry in in Table 5 would now be acceptable.  Semiderived fact types may easily be implemented in database systems by using two fact types, one for the asserted instances and one to include the derived instances.  There is no way in OWL of choosing between different implementation options for the subproperty proposition.

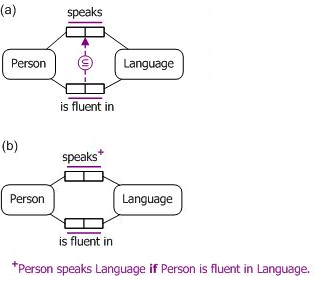
Figure 2.  (a) ORM model with a subset constraint; (b) ORM model with a semiderived fact type.

As a final example, consider the OWL ontology in Table 6.  Here the class Driver matches the set of individuals who drive some car, and the class MultiLinguist matches the set of individuals who speak at least two languages.  In the context of the predicate type declarations, and using "≡" for "if and only if" and "∃^2.." for the "there exists at least 2" numeric quantifier, these equivalency propositions may be formalized in logic as ∀x(Driver x ≡ ∃ y x drives y) and ∀x(MultiLinguist x ≡ ∃^2..y x speaks y).

If we assert that Terry drives a specific car and speaks at least two specific languages, the system will infer that Terry is a driver and a multilinguist.  An ORM model using derived subtypes for this situation is shown in Figure 3(a).

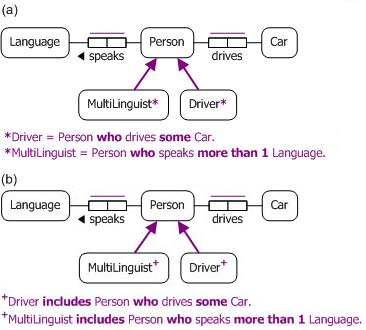
Figure 3.  (a) ORM model with derived subtypes; (b) ORM model with semiderived subtypes.

The ORM schema in Figure 3(b) shows an alternative implementation choice, using semiderived subtypes.  This allows us to simply assert that Terry is a driver and that Terry is a multilinguist without providing specific cars and languages for those facts.  The OWL ontology itself also allows this possibility.  For example, if we simply assert the following facts, the system will infer that Terry drives some car (yet to be explicitly named) and speaks at least two languages (currently unnamed).  Of course, if a specific drives fact and two specific speaks facts are supplied for Terry, the system will also infer that Terry is a driver and a multilinguist.

OWL itself has no support for choosing between such alternative implementations of the equivalency propositions.  Given that implementation choices often do matter in practice, especially for database applications, some proposals have been made to extend OWL with the ability to classify Tbox propositions as either derivation rules or as constraints (e.g., see [13]).

Conclusion

The current article discussed the logical status of structural statements in OWL 2, contrasting this with other data modeling and database approaches that support both integrity constraints and derivation rules.  The next article examines further advanced aspects of OWL.

References

[1]  T.A. Halpin & T. Morgan.  Information Modeling and Relational Databases, 2nd edition.  Morgan Kaufmann:  San Francisco (2008).  

[2]  T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol. 10, No. 9 (Sep. 2009), URL:  http://www.BRCommunity.com/a2009/b496.html  

[3]  T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol. 10, No. 12 (Dec. 2009), URL:  http://www.BRCommunity.com/a2009/b513.html  

[4]  T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol. 11, No. 3 (Mar. 2010), URL:  http://www.BRCommunity.com/a2010/b527.html  

[5]  T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol. 11, No. 6 (Jun. 2010), URL:  http://www.BRCommunity.com/a2010/b539.html  

[6]  T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol. 11, No. 12 (Dec. 2010), URL:  http://www.BRCommunity.com/a2010/b570.html  

[7]  T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol. 12, No. 2 (Feb. 2011), URL:  http://www.BRCommunity.com/a2011/b579.html  

[8]  T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol. 12, No. 6 (Jun. 2011), URL:  http://www.BRCommunity.com/a2011/b602.html  

[9]  T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol. 12, No. 9 (Sep. 2011), URL:  http://www.BRCommunity.com/a2011/b614.html  

[10]  T.A. Halpin, "Ontological Modeling (Part 9)," Business Rules Journal, Vol. 12, No. 12 (Dec. 2011), URL:  http://www.BRCommunity.com/a2011/b629.html  

[11]  Terry Halpin, "Ontological Modeling (Part 10)," Business Rules Journal, Vol. 13, No. 3 (Mar. 2012), URL:  http://www.BRCommunity.com/a2012/b644.html  

[12]  Krötzsch, M., Simancik, F.,  & Horrocks, I.  2012, "A Description Logic Primer," eprint arXiv:1201.4089, URL:  http://arxiv.org/abs/1201.4089  

[13]  Motik, B., Horrocks, I.,  & Sattler, U.  2009, "Bridging the Gap Between OWL and Relational Databases," J.  of Web Semantics, 7(2):74-89, April 2009.  

[14]  Object Management Group.  UML 2.0 Superstructure Specification.  Object Management Group (2003).  URL:  http://www.omg.org/uml  

[15]  W3C.  OWL 2 Web Ontology Language:  Primer.  W3C (2009).  URL:  http://www.w3.org/TR/owl2-primer/  

[16]  W3C.  OWL 2 Web Ontology Language:  Direct Semantics.  W3C (2009).  URL:  http://www.w3.org/TR/owl2-direct-semantics/  

[17]  W3C.  OWL Web Ontology Language Manchester Syntax.  W3C (2009).  URL:  http://www.w3.org/TR/owl2-manchester-syntax/  

[18]  W3C.  OWL Web Ontology Language Structural Specification and Functional-Style Syntax.  W3C (2009).  URL:  http://www.w3.org/TR/owl2-syntax/  

# # #