Ontological Modeling (Part 13)
This is the thirteenth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL).
The first article[3] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[4] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[5] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[6] discussed basic features of OWL, mainly using Manchester syntax. The fifth article[7] discussed OWL taxonomy, comparison operators for classes, data types, and predicates, and examined inverses, functional roles, and keys in more depth. The sixth article[8] covered cardinality restrictions in OWL 2. The seventh article[9] discussed the union, intersection, and complement operators in OWL 2. The eighth article[10] explored support for ring constraints within OWL 2. The ninth article[11] discussed enumerated types as well as value restrictions on properties in OWL 2. The tenth article[12] examined OWL 2's support for property chains, and compared this with related concepts in data modeling approaches. The eleventh article[13] reviewed the logical status of structural statements in OWL 2, contrasting this with other data modeling approaches that support both integrity constraints and derivation rules.
The twelfth article[14] discussed how to express negated facts in OWL 2 and avoid circularity when declaring subproperty chains. The current article provides a detailed comparison of the ways in which OWL 2, ORM, Barker ER, UML 2.5, and relational databases support simple identifiers.
Simple Identifiers
Figure 1(a) models some ways to refer to a country using the Object-Role Modeling (ORM) notation.[2] Let's assume that the model documentation declares that country codes are ISO 3166 alpha-2 codes (e.g., "AU" for Australia and "US" for the United States of America) and that ISO names are used for country names. The reference mode "(.code)" indicates that countries are primarily identified by their country code, so each country has exactly one country code (for this model we ignore other country codes such as ISO 3166 alpha-3 codes), and each country code refers to at most one country.
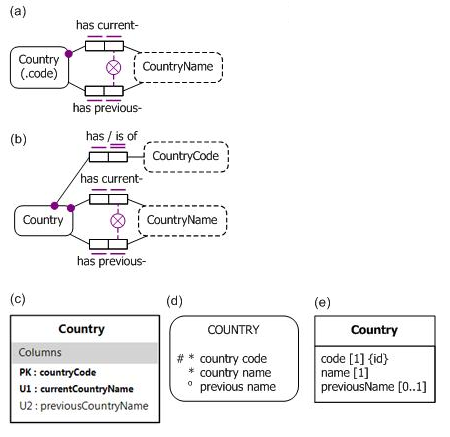
Figure 1. A schema in (a) compact ORM, (b) explicit ORM, (c) Relational, (d) Barker ER, and (e) UML notation.
The large dot attached to the Country role of the fact type Country has current-CountryName depicts the mandatory role constraint "Each Country has some current CountryName". Each bar next to a role depicts a uniqueness constraint on its role, so the current name relationship is one-to-one (each country has at most one current country name, and vice versa). The fact type Country has previous-CountryName is also one-to-one, but is optional for Country. Only a few countries have a previous name (e.g., Sri Lanka was called "Ceylon" until 1972, and Myanmar formerly had the ISO country name "Burma"). The circled "X" denotes the exclusion constraint that no country name is both a current and a previous ISO country name.
The Country(.code) reference mode notation is a convenient abbreviation for the mandatory 1:1 fact type Country has CountryCode shown in Figure 1(b), where the uniqueness constraint on the role of the CountryCode value type is chosen for the preferred or primary identifier (as indicated by a double bar). In ORM, the simplest kind of identification scheme for an entity type is a mandatory, 1:1 relationship from the entity type to a value type. In this example, each of the country code and current country name relationships provide such a simple identification scheme for Country. The previous country name relationship is not an identification scheme for Country, since not all instances of Country have to participate in this relationship. Nevertheless, previous country names are identifiers for those countries that have a previous name.
Figure 1(c) displays the relational database schema diagram generated from the ORM schema using the NORMA tool,[16] an open source plug-in to Microsoft Visual Studio. The table scheme for Country has three columns (a.k.a. attributes). The countryCode and currentCountryName attributes are in bold type, indicating that they are mandatory (not nullable). The previousCountryName attribute is unbolded, so is optional (nullable). The "PK" marks countryCode as a primary key component for Country. Since no other columns in Country are marked "PK", countryCode is the whole primary key of that table. The "U1" on the currentCountryName column marks it as a component of another uniqueness constraint (named U1 in the scope of this table). No other columns in the table are marked "U1", so entries in the currentCountryName column are unique (no duplicates). Since currentCountryName is also mandatory, it is an alternate key for Country. The "U2" applied just to the previousCountryName column indicates that its non-null entries are unique, so those countries that have a previous name can also be identified by that previous name.
Figure 1(d) depicts the example in the Barker Entity Relationship (ER) notation,[1] arguably the best of the popular, industrial versions of ER. The "#" on the country code attribute means that it is a component of the primary identifier for the Country entity type. In this case, it is the whole primary identifier. An asterisk "*" preceding an attribute indicates that it is mandatory for its entity type, and a small "o" indicates that the attribute is optional. Graphically, the only identifier that Barker ER can depict is the primary identifier, so it cannot mark the country name attribute as an alternate key. Nor can it display the uniqueness constraint on the non-null entries for the previous name attribute.
Figure 1(e) depicts the example as a class diagram in the Unified Modeling Language (UML) notation. Attribute multiplicities appear in square brackets after the attribute name. A multiplicity of 1 indicates that the attribute is mandatory and single valued, so each country has exactly one code and exactly one (current) name. A multiplicity of "0..1" means the attribute is optional and single-valued, so each country has at most one previous name. In 2011, UML version 2.4.1 introduced the capability to declare a class property (attribute or association end owned by the class) to be a component of a value-based identifier for the class. On a class diagram, the class property is annotated with an "{id}" modifier (in the UML metamodel, this sets the isID attribute of the property to true). The semantics of this feature remains the same in the latest version at the time of writing, UML 2.5 beta 1.[15] In Figure 1(e) the code attribute is the only one marked with "{id}" so this declares it as the natural identifier for the Country class. While UML does not require value-based identifiers to be declared, for human communication purposes such identifiers are essential.
UML allows at most one identification scheme per class to be depicted with the {id} modifier, so cannot graphically depict the name attribute as an alternate identifier for Country. Even if Class had no other identification schemes, we cannot use the {id} modifier to depict the previousName attribute as unique for its non-null entries, since UML does not allow all components of an {id} scheme to be optional.
Using techniques discussed in earlier articles, and ignoring the exclusion constraint between current and previous country names, the example may be specified in OWL as shown in Table 1. For readability, we consider only Manchester and Turtle syntax. We could shorten the code by assuming ISO alpha-2 codes (with implicit prefixes for the containing document) are used as Internationalized Resource Identifiers (IRIs) for countries, but let's assume other terms are used for the country IRIs (e.g., ":USA" for the United States of America, ":Oz" for Australia). Many country names contain embedded spaces (e.g., "Czech Republic") so can't be used directly as IRIs (though modified names using underscores or hyphens for spaces could be).
In practice, many OWL ontologies use meaningless, automatically generated identifiers as IRIs just as some relational database designers prefer artificial, surrogate keys for their table schemes. Human-readable labels can be associated with IRIs using rdfs:label annotation properties, and OWL software tools such as Protégé (http://protege.stanford.edu/) can be configured to display labels instead of IRIs to make the ontologies more readable.
Our decision in OWL to use IRIs to identify all countries of interest is not reflected in the Figure 1 data models, which are designed for database applications where country codes are standardly used to identify countries. As discussed further later, declaration of HasKey properties for a class is relevant only for the class individuals with IRIs explicitly declared.
|
Manchester Syntax |
Turtle Syntax |
|
DataProperty: hasCountryCode |
:hasCountryCode a owl:DatatypeProperty, |
In OWL, declaring a predicate as a HasKey property is similar to saying that it is inverse functional (in ORM terms, this simply adds a uniqueness constraint to the second role of the predicate). For example, "HasKey: hasCountryCode" declares that each character string is the country code of at most one named country. The HasKey feature has to be used for this declaration, since OWL does not allow data properties (that relate individuals to literals) to be directly declared as inverse functional properties (e.g., using the InverseFunctional characteristic in Manchester syntax, or owl:InverseFunctionalProperty in Turtle syntax).
However, OWL does allow object properties (that relate individuals to individuals) to be directly declared inverse functional. Recall that in OWL an individual may be named (identified by an IRI) or unnamed (represented by a blank node). This allows OWL to capture identification schemes that identify individuals by relating them directly to other individuals.
For example, the schemas in Figure 2 identify top politicians (e.g., presidents or prime ministers) by the country that they head (as chief politician). In the ORM schema of Figure 2(a), this is modeled using the mandatory 1:1 fact type TopPolitician heads Country, with the double-bar indicating the uniqueness constraint for the preferred identifier. For simplicity, the value constraint on gender codes ('M', 'F' for males and females) is omitted. This schema allows us to record the current facts that the top politician of the USA is male and the top politician of Australia is female, without knowing their names ('Barack Obama' and 'Julia Gillard').
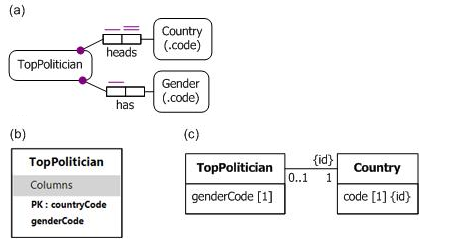
Figure 2. Identifying top politicians by the country they head, using (a) ORM, (b) Relational, and (c) UML notation.
Figure 2(b) shows the relational schema generated from the ORM schema using the NORMA tool. Here the countryCode primary key is used to identify the top politicians. For example, the two facts mentioned earlier may be entered as the tuples ('US', 'M') and ('AU', 'F'), respectively. Figure 2(c) shows a UML class diagram for this example, using the {id} modifier to mark the association end TopPolitican.country as the identifier for instances of the TopPolitician class.
Although Barker ER allows relationships as components of a composite primary identifier, it does not cater for cases like this where a single relationship provides the whole identifier [1, p. 3-13]. So, Barker ER does not support this kind of identification scheme.
Table 2 shows one way to code the TopPolitician schema in OWL, using Manchester or Turtle syntax. Here we assume that instances of Country and Gender have IRIs other than codes (e.g., :USA, :male). The identification scheme for TopPolitician is captured by specifying the object property headsCountry as an injective (mandatory, 1:1 into) relationship from TopPolitician to Country by declaring its minCardinality to be 1 and characterizing the predicate as both functional and inverse functional. Because the headsCountry predicate is an object property rather than a data property, its inverse functional nature can be directly declared without classifying it as a HasKey property.
|
Manchester Syntax |
Turtle Syntax |
|
DataProperty: hasCountryCode |
:hasCountryCode rdfs:domain :Country ; |
Although the OWL code in Table 1 and Table 2 provides a reasonable way to emulate the data models in Figure 1 and Figure 2, the semantics are not precisely the same. As discussed in a previous article [13], constraints specified in data models are not translated into actual constraints in OWL, but rather logical propositions that are understood in terms of open world semantics where some individuals may be unnamed. For example, declaring the subclass restriction "hasCountryCode min 1" for Country simply says that each country has a country code—it doesn't require the system to know what that code is. The next section further illustrates how OWL's support for unnamed individuals differs from what might be intuitively expected by users of typical database systems.
HasKey vs. InverseFunctional
Declaring a predicate to be InverseFunctional in OWL is not quite the same as declaring a predicate to be a HasKey property. A declared InverseFunctional characteristic applies to the predicate for all its applicable subject classes, whereas each HasKey declaration applies to only a single subject class or class expression. Moreover, an InverseFunctional characteristic may be applied only to an object property, whereas both object properties and data properties can be declared as HasKey properties. Another important difference is that the uniqueness aspect of HasKey applies only to named individuals (i.e., individuals that are explicitly named by an IRI in the Abox (the set of fact assertions)). In contrast, InverseFunctional declarations apply to any kind of individual (named individuals, anonymous individuals, and individuals whose existence is implied by existential quantification).[20, sec. 9.5]
We now illustrate this third difference with some simple examples. Consider the ORM schema displayed in Figure 3(a), which is used to record where politicians are born. In this case, we identify politicians simply by their IRIs (e.g., d:Obama, where d is the part of the IRI for the relevant document—in the following code, we as usual assume the current document, so "Obama" (in Manchester syntax) or ":Obama" (in Turtle) would suffice). In Figure 3(a) the lack of special punctuation (e.g., a dot or colon) in the reference mode "(IRI)" indicates that this is a general reference mode, so the value type IRI shown explicitly in Figure 3(b) can also be used to identify other entity types if desired. However, in this ORM model countries are identified by their country codes. In OWL, an entity can have multiple IRIs (e.g., :Venus owl:sameAs :TheMorningStar), but in this ORM model each politician has only one IRI. In ORM, fact roles may optionally be named, with their name displayed in square brackets beside the role (e.g., "birthCountry").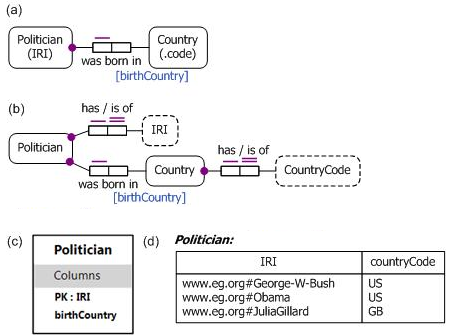
Figure 3. (a) Compact ORM schema, (b) expanded ORM schema, (c) relational schema, (d) sample data.
Figure 3(c) shows the relational database table scheme Politician (IRI, birthCountry) that NORMA generates from the ORM schema. Figure 3(d) shows the relational table populated with some sample data tuples ('http://eg.org/#George-W-Bush', 'US'), ('http://eg.org/#Obama', 'US'), and ('http://eg.org/#JuliaGillard', 'GB') to record the facts that George W. Bush and Obama were born in the USA, and Julia Gillard was born in the United Kingdom. While this varied choice of identifiers for politicians and countries might be unusual, it is nevertheless possible to model things this way in data modeling approaches such as ORM, ER, UML, and relational databases. Now let's consider how one might model this example in OWL.
The schema itself may be coded as shown in Table 3. In OWL, each class (in this case, Politician and Country) is typically understood to have an identification scheme based on IRIs. Although hasCountryCode is declared as a HasKey property for Country, each named individual that is an instance of Country has to be explicitly identified by an IRI in the fact base.
|
Manchester Syntax |
Turtle Syntax |
|
ObjectProperty: wasBornInCountry |
:wasBornInCountry rdfs:domain :Politician ; |
Given the schema in Table 3, the code in Table 4 asserts that Julia Gillard was born in some country that has country code "GB". We could assert this without knowing which country has that country code. In Manchester syntax, we've used the nodeID "_:c1" as an anonymous variable for the unnamed country. As an alternative, we could instead use the following code:
Individual: JuliaGillard Types: wasBornInCountry some
( hasCountryCode value "GB").
|
Manchester Syntax |
Turtle Syntax |
|
Individual: JuliaGillard |
:TheUK :hasCountryCode "GB". |
Now suppose we discover that the United Kingdom has the country code "GB" (chosen by ISO based on the long name "The United Kingdom of Great Britain and Northern Ireland"). Let's choose "TheUK" as an intuitive IRI fragment for the United Kingdom. We can now add the code shown in Table 5 to assert that the UK has the country code "GB".
|
Manchester Syntax |
Turtle Syntax |
|
Individual: TheUK |
:TheUK :hasCountryCode "GB". |
Given the OWL code in Table 3, Table 4, and Table 5, one might expect that it is correct to infer the fact that Julia Gillard was born in the United Kingdom, which may be expressed in Turtle thus:.
:JuliaGillard :wasBornInCountry :The UK.
However, this fact does not follow! This is because HasKey declarations apply only to named individuals (those with IRIs explicitly asserted). So ":Country owl:hasKey ( :hasCountryCode )." says that at most one named individual has a given country code, while allowing that there could be many unnamed individuals with that same country code. The assertion ":JuliaGillard :wasBornInCountry [ :hasCountryCode "GB "]." says that Julia Gillard was born in some (i.e., at least one, perhaps more) country (which might be named or unnamed) that has the country code "GB". So it is wrong to assume that this is the same as the named country (:TheUK) that has that country code.
This restriction of HasKey semantics to named individuals is designed to help ensure that inference rules using HasKey properties are "DL-safe" [18, sec. 9.5], so they will execute in a finite time. The basic idea is that we can explicitly name only a finite set of individuals, so by restricting rules to that input and applying only "finite operations" we ensure that the output from the rule is finite also.
Now consider the ORM schema in Figure 4(a). Here top politicians are identified by the country that they head, and their birth countries are also recorded. The birthcountry fact type is given a forward reading "TopPolitician heads Country" and an inverse reading "Country is headed by TopPolitician". The fact roles played by instances of Country are named to determine the column names generated by NORMA for the relational schema shown in Figure 4(b). A sample population of the relational database table is shown in Figure 4(c). The tuple ('AU', 'GB") in the sample data records the fact that the top politician of Australia was born in the United Kingdom (to be more precise, Julia Gillard, the prime minister of Australia, was born in Wales).
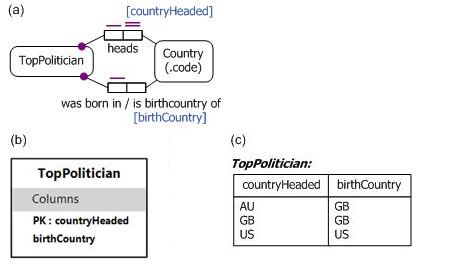
Figure 4. (a) An ORM schema, (b) its generated relational schema, and (c) a sample table population.
Table 6 shows one way to code the schema in OWL. The uniqueness constraint on the countryHeaded fact role in Figure 4(a) is captured by the inverse functional declaration for the headsCountry predicate.
|
Manchester Syntax |
Turtle Syntax |
|
ObjectProperty: wasBornInCountry |
:wasBornInCountry rdfs:domain :TopPolitician ; |
Suppose we now add the facts shown in Table 7. The first fact uses a blank node to state that something (we know this is a top politician because of the earlier domain declaration) heads the country Australia and was born in the United Kingdom. The second fact says that Julia Gillard heads the country Australia. An alternative way to express the first fact in Manchester syntax is:
Individual: TheUK Types: isBirthCountryOf some
( headsCountry Australia).
Manchester Syntax |
Turtle Syntax |
|
Individual: _:p |
:wasBornInCountry rdfs:domain :TopPolitician ; |
Unlike HasKey declarations, the inverse functional characteristic of headsCountry applies to all individuals, not just named individuals. So from the above facts, the following fact may be inferred (Manchester syntax shown on the left, Turtle syntax of the right).
| Individual: JuliaGillard | :JuliaGillard :wasBornInCountry :TheUK. |
| Facts: wasBornInCountry TheUK |
Conclusion
The current article compared the different ways in which OWL 2, ORM, Barker ER, and UML support simple identifiers. Compound identification schemes in OWL were briefly discussed in [7], but there is more to the story. The next article contrasts the support provided in OWL 2 and popular data modeling approaches for complex cases of identification schemes (compound identifiers, disjunctive reference, and context-dependent reference).
References
[1] R. Barker. CASE*Method: Tasks and Deliverables. Addison-Wesley: Wokingham, England (1990). ![]()
[2] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[3] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html
![]()
[4] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html [Erratum: In the original version of the second article in this series, the discussion of transitivity of subclassing incorrectly used "a" instead of "rdfs:subClassOf" in the inference example for MaleSinger, Singer, and Person.]
![]()
[5] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[7] T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol.
11, No. 12 (Dec. 2010), URL: http://www.BRCommunity.com/a2010/b570.html
![]()
[8] T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol.
12, No. 2 (Feb. 2011), URL: http://www.BRCommunity.com/a2011/b579.html
![]()
[9] T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol.
12, No. 6 (Jun. 2011), URL: http://www.BRCommunity.com/a2011/b602.html
![]()
[10] T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol.
12, No. 9 (Sep. 2011), URL: http://www.BRCommunity.com/a2011/b614.html
![]()
[11] T.A. Halpin, "Ontological Modeling (Part 9)," Business Rules Journal, Vol. 12, No. 12 (Dec. 2011), URL: http://www.BRCommunity.com/a2011/b629.html
![]()
[12] T.A. Halpin, "Ontological Modeling (Part 10)," Business Rules Journal, Vol. 13, No. 3 (Mar. 2012), URL: http://www.BRCommunity.com/a2012/b644.html
![]()
[13] T.A. Halpin, "Ontological Modeling (Part 11)," Business Rules Journal, Vol. 13, No. 6 (Jun. 2012), URL: http://www.BRCommunity.com/a2012/b657.html
![]()
[14] T.A. Halpin, "Ontological Modeling (Part 12)," Business Rules Journal, Vol. 13, No. 11 (Nov. 2012), URL: http://www.BRCommunity.com/a2012/b678.html
![]()
[15] Object Management Group. OMG Unified Modeling Language Specification (OMG UML), version 2.5 FTF Beta 1.
Object Management Group (2012). Available online at:
http://www.omg.org/spec/UML/2.5/ ![]()
[16] NORMA tool (www.ORMSolutions.com) available online at
www.ORMFoundation.org ![]()
[17] W3C. OWL 2 Web Ontology Language: Primer (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-primer/
[18] W3C. OWL 2 Web Ontology Language: Direct Semantics (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-direct-semantics/
[19] W3C. OWL Web Ontology Language Manchester Syntax (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[20] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax (Second Edition).
W3C (2012). URL: http://www.w3.org/TR/owl2-syntax/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules