Ontological Modeling (Part 14)
This is the fourteenth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL).
The first article[3] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[4] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[5] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[6] discussed basic features of OWL, mainly using Manchester syntax. The fifth article[7] discussed OWL taxonomy, comparison operators for classes, data types, and predicates, and examined inverses, functional roles, and keys in more depth. The sixth article[8] covered cardinality restrictions in OWL 2. The seventh article[9] discussed the union, intersection, and complement operators in OWL 2. The eighth article[10] explored support for ring constraints within OWL 2. The ninth article[11] discussed enumerated types as well as value restrictions on properties in OWL 2. The tenth article[12] examined OWL 2's support for property chains, and compared this with related concepts in data modeling approaches. The eleventh article[13] reviewed the logical status of structural statements in OWL 2, contrasting this with other data modeling approaches that support both integrity constraints and derivation rules.
The twelfth article[14] discussed how to express negated facts in OWL 2 and avoid circularity when declaring subproperty chains. The thirteenth article[15] provided a detailed comparison of the ways in which OWL 2, ORM, Barker ER, UML 2.5, and relational databases support simple identifiers. The current article discusses modeling of unary facts, and extends the comparison of identification schemes in [16] by considering one complex case of reference schemes (compound identifiers).
Unary Facts
Figure 1(a) depicts a simple data model about hospital patients in the graphical notation of Object-Role Modeling (ORM).[2] Each patient is identified by a patient number and has exactly one patient name (not necessarily identifying). The fact type Patient smokes is used to record which patients smoke. Sample data are provided in the fact tables. The entry 102 in the fact table for Patient smokes indicates that Patient 102 smokes. This model adopts closed world semantics, so the absence of an entry for patients 101 and 102 in this fact table indicates that patients 101 and 103 do not smoke. The fact type Patient smokes is said to be a unary fact type because its logical predicate (smokes) is unary (i.e., has a single argument). Figure 1(b) and Figure 1(c) show equivalent schemas without the sample data in the notation of Barker ER[1] and UML[17] respectively. Both of these capture smoking facts by using a Boolean attribute (e.g., Patient.isSmoker). Alternatively, all three notations could model smoking facts by introducing a Smoker subtype/subclass of Patient.
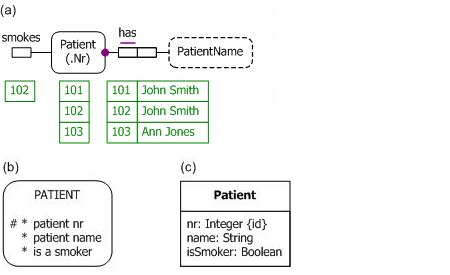
Figure 1. A simple Patient model in the graphical notation of (a) ORM, (b) Barker ER, and (c) UML.
Previous articles in this series discussed how to model subtyping and binary relationships in OWL, but not unary facts expressed as unary relationships (e.g., Patient 102 smokes) or Boolean attribute assignments (e.g., 102:Patient.isSmoker = true). Recall that all facts in OWL must be expressed subject-predicate-object triples, where the predicate is a binary relationship. Hence, unary facts are expressed in OWL by using a binary predicate to relate the subject to an object that is either a Boolean value (true or false) or a status value with two possibilities (e.g., "Smoker", "NonSmoker").
Table 1 shows an OWL encoding of the model in Figure 1 using the data property isSmoker to map patients onto Boolean values (see the code highlighted in italics). We assert that patient 102 smokes by mapping its isSmoker data property to the value true. OWL adopts open world semantics, so the absence of a proposition (e.g., Patient 101 smokes) does not imply that the proposition is false. To match the models shown in Figure 1, we need to apply closed world semantics for smoking facts. We therefore make the isSmoker data property mandatory (minimum multiplicity of 1) for Patient, and explicitly assert that patients 101 and 103 do not smoke by mapping their isSmoker data property to the value false.
|
Manchester Syntax |
Turtle Syntax |
|
DataProperty: hasPatientNr |
:hasPatientNr a owl:DatatypeProperty , |
|
DataProperty: hasPatientName |
:hasPatientName a owl:DatatypeProperty , |
|
DataProperty: isSmoker |
:isSmoker a owl:DatatypeProperty ; |
|
Class: Patient |
:Patient owl:hasKey ( :hasPatientNr ) ; |
|
Individual: Patient101 |
:Patient101 a :Patient , |
|
Individual: Patient102 |
:Patient102 a :Patient , |
|
Individual: Patient103 |
:Patient103 a :Patient , |
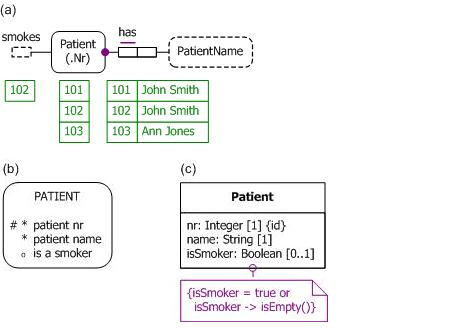
Figure 2. Adopting open world semantics for smoking facts in (a) ORM, (b) Barker ER, and (c) UML.
Figure 2(a) shows an ORM model where open world semantics is adopted for the fact type Patient smokes, as shown by the dashed (and hence open) line for the smokes predicate. In this case, the absence of entries for 101 and 103 in the smokes fact table indicates that it is unknown whether they smoke. In this model, there is no way to explicitly assert that a given patient does not smoke. Figure 2(b) partly captures this in the Barker ER version of the model by indicating that the "is a smoker" attribute is optional (as indicated by the preceding "o" instead of "*"). We also need to ensure that the only values allowed for this attribute are true and null, but the Barker ER notation does not display this on the diagram. Figure 2(c) fully captures the semantics in UML by assigning a multiplicity of [0..1] to the isSmoker attribute and adding a note to prevent the attribute being assigned the value false.
The open world semantics model in Figure 2(a) may be coded in OWL by modifying the code shown in Table 2 as follows: remove the minimum multiplicity of 1 restriction on the isSmoker data property; remove the "isSmoker false" fact assertions for patients 101 and 103.
Figure 3(a) shows an ORM model where open world with negation semantics is adopted for the fact type Patient smokes, as shown by the tilde "~"(a logical symbol for negation) inside the dashed line box for the smokes predicate. In this case, the entry "~101" in the smokes fact table indicates that patient 101 does not smoke, the 102 entry indicates that patient 102 does smoke, and the absence of an entry for 103 in the smokes fact table indicates that it is unknown whether patient 103 smokes. Figure 3(b) and Figure 3(c) show the equivalent schemas in Barker ER and UML respectively: the isSmoker attribute is optional but may be assigned true or false where known.
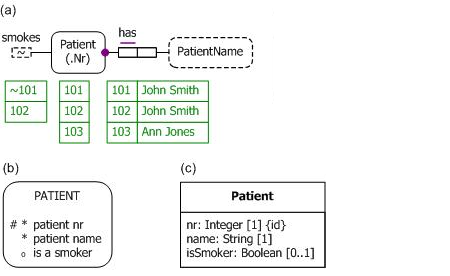
Figure 3. Adopting open world with negation semantics for smoking facts in (a) ORM, (b) Barker ER, and (c) UML.
The open world with negation semantics model in Figure 3(a) may be coded in OWL by modifying the code shown in Table 2 as follows: remove the minimum multiplicity of 1 restriction on the isSmoker data property; remove the "isSmoker false" fact assertion for patient 103.
As you can see, how unary facts are coded in OWL depends on how complete your knowledge is. If you have complete knowledge of the relevant property, choose the code for closed world semantics. If you know some instances where the property is true, and some where the property is false, but there are also some instances where you don't know the truth value of the property, then choose the code for open world with negation semantics. If you know some instances where the property is true but have no knowledge of where the property is false, then choose the code for simple, open world semantics. In practice, closed world semantics and open world with negation semantics are the most common cases.
Compound Identifiers
A compound reference scheme identifies entities of a given type by means of a combination of two or more attributes or relationships. For example, in the ORM schema of Figure 4(a), rooms are identified by combining their building number with their local room number (e.g., the room in building 1 with room number 205 is distinct from the room in building 2 with room number 205). The circled double bar denotes an external uniqueness constraint underlying this compound, preferred reference scheme for Room. This corresponds to fact verbalizations that identify rooms by compound definite descriptions (e.g., "the Room that is in the Building with BuildingNr 1 and has RoomNr 205").
The circled single bar depicts an external uniqueness constraint for a compound, alternate reference scheme for buildings based on a combination of their x and y coordinates. Buildings also have a simple, preferred reference scheme (based on building number). The unary fact type Room is windowed is used to record which rooms have a window.
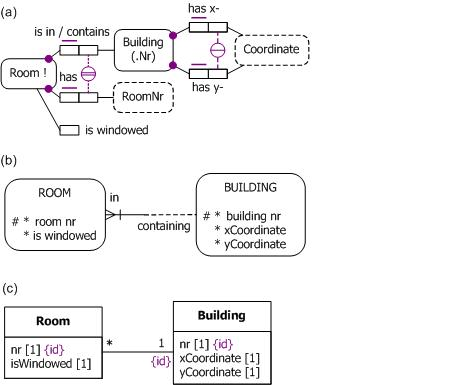
Figure 4. A compound reference scheme for rooms in the notation of (a) ORM, (b) Barker ER, and (c) UML.
Figure 4(b) shows a Barker ER schema for the same example. The composite reference scheme for Room is indicated by the # on the room nr attribute and the vertical stroke "|" through Room's role in its containment relationship with Building. The simple reference scheme for Building is captured by the # on the building nr attribute. However, Barker ER has no way to indicate that the building coordinate pair provides an alternate reference scheme for Building.
Figure 4(c) shows a UML class diagram for the same example. The composite reference scheme for Room is captured by marking the attribute Room.nr and the association end Room.building with the {id} modifier. The simple reference scheme for Building is indicated by the {id} modifier on Building.nr. However, UML cannot graphically depict that the coordinate combination is also unique for buildings.
Table 2 lists the OWL code for the model in Figure 4, along with a sample population. The isWindowed predicate is declared as a data property with domain Room and range xsd:Boolean, with individual facts using true or false as appropriate. For the external uniqueness constraints in Figure 4(a), composite HasKey properties are declared as shown in italics.
However, as explained in the previous article [15], these HasKey declarations have no effect on specific room or building instances unless an IRI is also explicitly declared for those instances. In this case, I've used meaningful IRIs (e.g., Room1-205 for room 205 in building 1). However, in cases where this is impractical (e.g., consider IRIs for street addresses), we could use surrogate identifiers (e.g., address_1, address_2, etc.) or instead simply abandon any attempt to capture the uniqueness semantics in the OWL ontology.
Manchester Syntax |
Turtle Syntax |
|
ObjectProperty: isInBuilding |
:isInBuilding a owl:FunctionalProperty , |
|
ObjectProperty: containsRoom |
:containsRoom a owl:ObjectProperty ; |
|
DataProperty: hasBuildingNr |
:hasBuildingNr a owl:DatatypeProperty , |
|
DataProperty: hasXcoordinate |
:hasXcoordinate a owl:DatatypeProperty , |
|
DataProperty: hasYcoordinate |
:hasYcoordinate a owl:DatatypeProperty , |
|
DataProperty: hasRoomNr |
:hasRoomNr a owl:DatatypeProperty , |
|
DataProperty: isWindowed |
:isWindowed a owl:DatatypeProperty , |
|
Class: Building |
:Building a owl:Class ; |
|
Class: Room |
:Room a owl:Class ; |
|
Individual: Building1 |
:Building1 a :Building , |
|
Individual: Building2 |
:Building2 a :Building , |
|
Individual: Room1-205 |
:Room1-205 a :Room , |
|
Individual: Room2-205 |
:Room2-205 a :Room , |
Conclusion
The current article discussed how to model unary facts in ORM, Barker ER, and UML, and how to encode them in OWL by using data properties with a Boolean range. It also compared the different ways in which ORM, Barker ER, UML, and OWL support compound identification schemes. The next article discusses how these various modeling notations support more complex kinds of identification schemes (viz. disjunctive reference and context-dependent reference).
References
[1] R. Barker. CASE*Method: Tasks and Deliverables. Addison-Wesley: Wokingham, England (1990). ![]()
[2] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[3] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html
![]()
[4] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html [Erratum: In the original version of the second article in this series, the discussion of transitivity of subclassing incorrectly used "a" instead of "rdfs:subClassOf" in the inference example for MaleSinger, Singer, and Person.]
![]()
[5] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[7] T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol.
11, No. 12 (Dec. 2010), URL: http://www.BRCommunity.com/a2010/b570.html
![]()
[8] T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol.
12, No. 2 (Feb. 2011), URL: http://www.BRCommunity.com/a2011/b579.html
![]()
[9] T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol.
12, No. 6 (Jun. 2011), URL: http://www.BRCommunity.com/a2011/b602.html
![]()
[10] T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol.
12, No. 9 (Sep. 2011), URL: http://www.BRCommunity.com/a2011/b614.html
![]()
[11] T.A. Halpin, "Ontological Modeling (Part 9)," Business Rules Journal, Vol. 12, No. 12 (Dec. 2011), URL: http://www.BRCommunity.com/a2011/b629.html
![]()
[12] T.A. Halpin, "Ontological Modeling (Part 10)," Business Rules Journal, Vol. 13, No. 3 (Mar. 2012), URL: http://www.BRCommunity.com/a2012/b644.html
![]()
[13] T.A. Halpin, "Ontological Modeling (Part 11)," Business Rules Journal, Vol. 13, No. 6 (Jun. 2012), URL: http://www.BRCommunity.com/a2012/b657.html
![]()
[14] T.A. Halpin, "Ontological Modeling (Part 12)," Business Rules Journal, Vol. 13, No. 11 (Nov. 2012), URL: http://www.BRCommunity.com/a2012/b678.html
![]()
[15] T.A. Halpin, "Ontological Modeling (Part 13)," Business Rules Journal, Vol. 14, No. 3 (Mar. 2013), URL: http://www.BRCommunity.com/a2013/b693.html ![]()
[16] T.A. Halpin, "Modeling of Reference Schemes," BPMDS 2013 and EMMSAD 2013, eds. I. Bider et al. LNBIP 147, Springer-Verlag, Berlin Heidelberg (2013), pp. 308–323. ![]()
[17] Object Management Group. OMG Unified Modeling Language Specification (OMG UML), version 2.5 FTF Beta 1.
Object Management Group (2012). Available online at:
http://www.omg.org/spec/UML/2.5/ ![]()
[18] NORMA tool (www.ORMSolutions.com) available online at www.ORMFoundation.org
[19] W3C. OWL 2 Web Ontology Language: Primer (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-primer/
[20] W3C. OWL 2 Web Ontology Language: Direct Semantics (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-direct-semantics/
[21] W3C. OWL Web Ontology Language Manchester Syntax (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[22] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-syntax/
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules