Ontological Modeling (Part 15)
This is the fifteenth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL).
The first article[3] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[4] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[5] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[6] discussed basic features of OWL, mainly using Manchester syntax. The fifth article[7] discussed OWL taxonomy, comparison operators for classes, data types, and predicates, and examined inverses, functional roles, and keys in more depth. The sixth article[8] covered cardinality restrictions in OWL 2. The seventh article[9] discussed the union, intersection, and complement operators in OWL 2. The eighth article[10] explored support for ring constraints within OWL 2. The ninth article[11] discussed enumerated types as well as value restrictions on properties in OWL 2. The tenth article[12] examined OWL 2's support for property chains, and compared this with related concepts in data modeling approaches. The eleventh article[13] reviewed the logical status of structural statements in OWL 2, contrasting this with other data modeling approaches that support both integrity constraints and derivation rules.
The twelfth article[14] discussed how to express negated facts in OWL 2 and avoid circularity when declaring subproperty chains. The thirteenth article[15] provided a detailed comparison of the ways in which OWL 2, ORM, Barker ER, UML 2.5, and relational databases support simple identifiers. The fourteenth article[16] discussed modeling of unary facts, and extended the comparison of identification schemes to compound reference schemes in which all components are mandatory. The current article focuses on compound reference schemes in which some components are optional.
Join Semantics of External Uniqueness Constraints
Figure 1(a) depicts a fragment from the metamodel for Object-Role Modeling (ORM),[2] together with a sample fact population. A role is a part played in a fact type (relationship type). Each role and each fact type is primarily identified by a surrogate id (for discussion purposes these ids are displayed on the diagram). Each role occurs in exactly one fact type, and optionally may be given a role name. The sample data in the fact tables effectively populates the metamodel with itself. The fact table for fact type ft1 (with reading Role is in FactType) records that roles r1 and r2 are in fact type ft1, and roles r3 and r4 are in fact type ft2. The fact table for fact type ft2 (Role has Rolename) declares that role r4 has the role name 'name'.
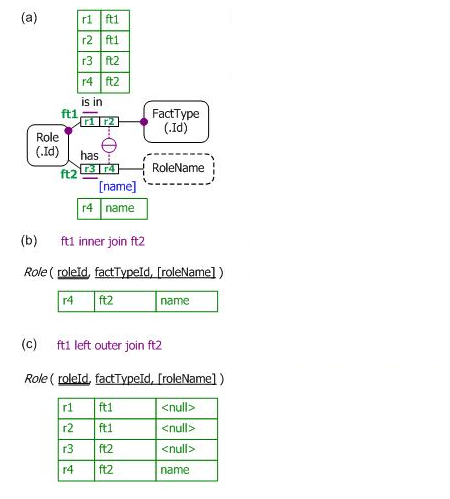
Figure 1. (a) An ORM metamodel fragment, and (b) the inner join and (c) outer join of its fact tables.
The circled bar in Figure 1(a) depicts an external uniqueness constraint to ensure that if a role does have a name, then the combination of that name and the role's fact type applies to only that role — in other words, no two roles in the same fact type can have the same name. Figure 1(b) shows the result of inner joining the fact tables for the fact types ft1 and ft2 on matching a role entry for r1 with a role entry for r3. As a match exists only for the entry r4, the inner join has only one row. In the relation scheme notation for the Role table, the primary key roleId is doubly underlined. The square brackets around "roleName" indicate that it is optional (nullable). Here the single underlining of the attribute pair factTypeId, roleName indicates that its pair entries are unique for those rows where roleName is not null. So for those roles that are named, the combination of their name and fact type provides a secondary reference scheme.
The populated ORM model in Figure 1(a) maps to the relational database table shown in Figure 1(c). The relational mapping performs an outer join from ft1 to ft2, so the resulting table includes four rows. This includes the inner join result, but adds rows for the entries r1, r2, and r3, where a match is not made, using a null entry for the role name. In the SQL standard, the uniqueness constraint on the factTypeId and roleName columns may be enforced by an assertion with the following body:
check (not exists
(select factTypeId, roleName from Role
where roleName is not null
group by factTypeId, roleName having count(*) > 1))
Notice that this restricts the rows to the inner join before checking for uniqueness. Although most commercial SQLs do not yet support assertions, they usually provide other ways to enforce the constraint, such as an appropriate trigger or a filtered index.
In ORM, an external uniqueness constraint depicted by a plain, circled bar is always interpreted with inner join semantics, not outer join semantics. Typically, the roles hosted by the referenced object type in its reference scheme are all mandatory, in which case inner join semantics is the only possibility. For example, see the compound reference scheme examples for Room and Building discussed in the previous article.[16]
However, if at least one of the roles in the reference scheme is optional, then in some cases inner join semantics applies, as in Figure 1(a) where r3 is optional, and in other cases outer join semantics applies, as in the ORM model in Figure 2(a). Here each course is primarily identified by its course code, but also has a course title. It is optional whether a course is offered by a department. For example, an inter-disciplinary course or a course offered by a visiting academic might not be associated with any specific department. The model is populated by three different courses, each of which has the same title 'Mechanics'.
The external uniqueness constraint in Figure 2(a) is depicted with an inner "o" through the uniqueness bar, indicating that the uniqueness constraint has outer join semantics, with the added proviso that nulls produced in the outer join are treated as actual values. Hence, in addition to being identified by its course code, each course that is offered by a department may be referenced by the combination of its course title and its department, e.g., (Mechanics, PY) and (Mechanics, MA). Each course offered by no department may be identified either by its code or its title.
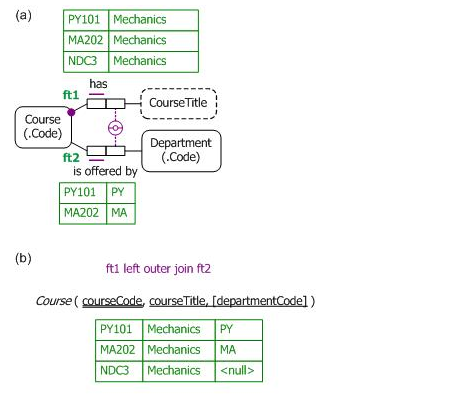
Figure 2. (a) An ORM model with an external uniqueness constraint with outer join semantics; (b) its relational map.
External uniqueness constraints of this nature are verbalized in two sentences, one for the inner join semantics and one for the additional semantics of the outer join. The external uniqueness constraint in Figure 2(a) verbalizes thus:
For each CourseTitle and Department,
at most one Course has that CourseTitle and is offered by that Department.
For each CourseTitle,
at most one Course has that CourseTitle and is offered by no Department.
Figure 3 shows an example of violating the external uniqueness constraint with outer join semantics. Adding the fact (shown in red color) that the course NDC4 has the title 'Mechanics' would result in two courses with the same title where the courses are offered by no department. In the outer join result shown in Figure 3(b), the pair ('Mechanics', <null>) appears twice, thus violating uniqueness (treating <null> as a normal value).
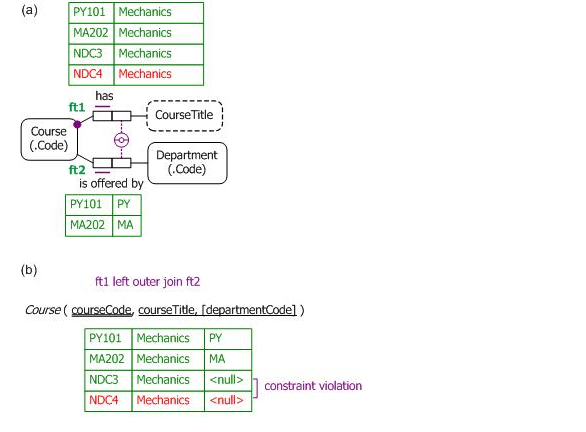
Figure 3. Adding the fact that course NDC4 has the title 'Mechanics' violates the external uniqueness constraint.
Neither the Unified Modeling Language (UML)[19] nor Entity Relationship Modeling (ER) dialects (e.g., Barker ER[1]) include a graphical notation to capture external uniqueness constraints involving optional roles, so we do not discuss them further here. However, we will now consider how to model such constraints in the Web Ontology Language (OWL).
External uniqueness constraints with inner join semantics may be declared in OWL by simply using compound HasKey properties on the referenced class, as discussed in earlier articles. For example, assuming the object property isInFactType and the data properties hasRoleId and hasRoleName, the reference schemes for Role in the ORM schema in Figure 1(a) may be specified in Manchester syntax as shown below. The external uniqueness constraint is captured in the final HasKey declaration, shown here in italics.
Class: Role
SubClassOf: hasRoleId min 1 xsd:string,
isInFactType min 1 FactType
HasKey: hasRoleId
HasKey: isInFactType, hasRoleName
Capturing external uniqueness constraints with outer join semantics in OWL requires more work. Typically, this will involve introducing a subclass for the instances that don't play the relevant optional role and then declaring a HasKey property for that subclass. To ensure that the HasKey declarations are affective, IRIs must be included for the referenced instances. For example, Table 1 shows an OWL encoding of the model in Figure 2(a), using IRIs such as Course-PY101 and Physics-Department for courses and departments. The subclass NonDepartmentalCourse is added for courses offered by no department, and hasCourseTitle is declared as a HasKey property for it (shown here in italics).
|
Manchester Syntax |
Turtle Syntax |
|
DisjointClasses: Course, Department |
|
|
ObjectProperty: isOfferedBy |
:isOfferedBy a owl:FunctionalProperty , |
|
DataProperty: hasCourseTitle |
:hasCourseTitle a owl:DatatypeProperty , |
|
DataProperty: hasCourseCode |
:hasCourseCode a owl:DatatypeProperty , |
|
DataProperty: hasDepartmentCode |
:hasDepartmentCode a owl:DatatypeProperty , |
|
Class: Course |
:Course a owl:Class ; |
|
Class: Department |
:Department a owl:Class ; |
|
Class: NonDepartmentalCourse |
:NonDepartmentalCourse a owl:Class ; |
|
Individual: Mathematics-Department |
:Mathematics-Department a :Department , |
|
Individual: Physics-Department |
:Physics-Department a :Department , |
|
Individual: Course-PY101 |
:Course-PY101 a :Course , |
|
Individual: Course-MA202 |
:Course-MA202 a :Course , |
|
Individual: Course-NDC3 |
:Course-NDC3 a :NonDepartmentalCourse , |
If we now add the test data shown in Table 2, this will violate the HasKey condition that non-departmental courses can be identified by their titles, since two non-departmental courses, NDC3 and NDC4, would have the same title 'Mechanics'.
Manchester Syntax |
Turtle Syntax |
|
Individual: Course-NDC4 |
:Course-NDC4 a :NonDepartmentalCourse , |
If you are using the free Protégé tool for OWL (http://protege.stanford.edu/), you will need to run one of its inbuilt reasoners before the violation is detected. In Protégé, ontologies may be entered using its graphical user interface or by opening a text file with the OWL code for the ontology. If you wish to use the OWL code supplied in tables in this series of articles, you should include relevant prefix abbreviations at the start of the file. In Manchester syntax you can use the following.
Prefix: : <http://eg.org#>
Prefix: dc: <http://purl.org/dc/elements/1.1/>
Prefix: owl: <http://www.w3.org/2002/07/owl#>
Prefix: rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#>
Prefix: xml: <http://www.w3.org/XML/1998/namespace>
Prefix: xsd: <http://www.w3.org/2001/XMLSchema#>
Prefix: rdfs: <http://www.w3.org/2000/01/rdf-schema#>
For Turtle, you can use the following:
@prefix : <http://eg.org#> .
@prefix dc: <http://purl.org/dc/elements/1.1/> .
@prefix owl: <http://www.w3.org/2002/07/owl#> .
@prefix rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#> .
@prefix xml: <http://www.w3.org/XML/1998/namespace> .
@prefix xsd: <http://www.w3.org/2001/XMLSchema#> .
@prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#> .
@base <http://www.w3.org/2002/07/owl#> .
If you copy the code to a plain text editor, such as Wordpad, then save it with a ".owl" file extension, you can open the file in Protégé, and inspect the contents in its graphical interface. Then run the reasoner to check for inconsistencies such as the HasKey violation discussed above.
Disjunctive Reference Schemes
In a disjunctive reference scheme, instances of an entity type are identified by a logical disjunction of attributes or relationships, at least one of which is optional for the entity type, while the disjunction itself is mandatory for the entity type. In practice disjunctive reference schemes are typically used only for secondary reference, as in Figure 3(a). However, they may also be used for the preferred reference scheme. For example, if courses do not have course codes, we would identify some instances (the departmental courses) by combining their title and department, and identify the other instances (the non-departmental courses) simply by their title. An ORM schema for this situation is shown in Figure 4(a). In ORM, if an external uniqueness constraint with outer join semantics is used for a preferred reference scheme, it is depicted graphically by a circled, double-bar with an embedded "o".
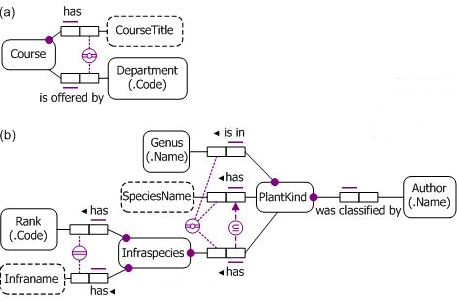
Figure 4. ORM models where the preferred reference scheme for Course and Plantkind is disjunctive.
Practical examples of disjunctive reference in industrial modeling include botanical classification schemes and complex addressing schemes. Figure 4(b) shows a simplified ORM model of the botanical case. Here some plant kinds are identified purely by their genus (e.g., Agrostis), some are identified by combining their genus and species name (e.g., Acacia interior), and others are identified by combining their genus, species name, and infraspecies (itself identified by combining rank and infraname), e.g., Eucalyptus fibrosa ssp. nubila.
Disjunctive reference schemes violate entity integrity (where all primary key components must be non-null), so cannot be implemented as primary keys in a pure relational model, but may be implemented in SQL systems since they do not require primary keys to be declared. For further discussion of this example, along with options for mapping it to a relational database, see [2, pp. 522-523]. In practice, it's usually best to introduce a simple identifier (e.g., CourseCode or PlantKindId), relegating the disjunctive scheme to secondary reference — in fact, this is required for implementing disjunctive reference in OWL, since HasKey properties are enforceable only on named individuals. The full treatment of the botanical classification model in [21] illustrates just how complex disjunctive reference schemes can be in practice.
Conclusion
The current article discussed compound reference schemes in which some components are optional, distinguishing cases where conceptually the underlying external uniqueness constraint has inner join or outer join semantics. Such cases can be depicted graphically in ORM, and coded in OWL by applying HasKey properties to subclasses that do not participate in relevant roles that are optional for their superclass, so long as all referenced individuals are named. Discussion of ORM support for other varieties of disjunctive reference schemes, as well as context-dependent reference may be found in [17, 18].
References
[1] R. Barker. CASE*Method: Tasks and Deliverables. Addison-Wesley: Wokingham, England (1990). ![]()
[2] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition. Morgan Kaufmann: San Francisco (2008).
[3] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html
![]()
[4] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html [Erratum: In the original version of the second article in this series, the discussion of transitivity of subclassing incorrectly used "a" instead of "rdfs:subClassOf" in the inference example for MaleSinger, Singer, and Person.]
![]()
[5] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[7] T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol.
11, No. 12 (Dec. 2010), URL: http://www.BRCommunity.com/a2010/b570.html
![]()
[8] T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol.
12, No. 2 (Feb. 2011), URL: http://www.BRCommunity.com/a2011/b579.html
![]()
[9] T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol.
12, No. 6 (Jun. 2011), URL: http://www.BRCommunity.com/a2011/b602.html
![]()
[10] T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol.
12, No. 9 (Sep. 2011), URL: http://www.BRCommunity.com/a2011/b614.html
![]()
[11] T.A. Halpin, "Ontological Modeling (Part 9)," Business Rules Journal, Vol. 12, No. 12 (Dec. 2011), URL: http://www.BRCommunity.com/a2011/b629.html
![]()
[12] T.A. Halpin, "Ontological Modeling (Part 10)," Business Rules Journal, Vol. 13, No. 3 (Mar. 2012), URL: http://www.BRCommunity.com/a2012/b644.html
![]()
[13] T.A. Halpin, "Ontological Modeling (Part 11)," Business Rules Journal, Vol. 13, No. 6 (Jun. 2012), URL: http://www.BRCommunity.com/a2012/b657.html
![]()
[14] T.A. Halpin, "Ontological Modeling (Part 12)," Business Rules Journal, Vol. 13, No. 11 (Nov. 2012), URL: http://www.BRCommunity.com/a2012/b678.html
![]()
[15] T.A. Halpin, "Ontological Modeling (Part 13)," Business Rules Journal, Vol. 14, No. 3 (Mar. 2013), URL: http://www.BRCommunity.com/a2013/b693.html ![]()
[16] T.A. Halpin, "Ontological Modeling (Part 14)," Business Rules Journal, Vol. 14, No. 9 (Sep. 2013), URL: http://www.BRCommunity.com/a2013/b720.html ![]()
[17] T.A. Halpin, "Modeling of Reference Schemes," BPMDS 2013 and EMMSAD 2013, eds. I. Bider et al. LNBIP 147, Springer-Verlag, Berlin Heidelberg (2013), pp. 308–323. ![]()
[18] T.A. Halpin & M. Curland. "Recent Enhancements to ORM," On the Move to Meaningful Internet Systems 2013: OTM 2013 Workshops, eds. Y.T. Demey and H. Panetto, Springer LNCS 8186 (2013), pp. 467-476. ![]()
[19] Object Management Group. OMG Unified Modeling Language Specification (OMG UML), version 2.5 FTF Beta 1.
Object Management Group (2012). Available online at:
http://www.omg.org/spec/UML/2.5/ ![]()
[20] NORMA tool (www.ORMSolutions.com) available online at www.ORMFoundation.org
[21] P. Ritson. Use of Conceptual Schemas for Relational Implementation. Doctoral dissertation, University of Queensland (1994). ![]()
[22] W3C. OWL 2 Web Ontology Language: Primer (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-primer/
[23] W3C. OWL 2 Web Ontology Language: Direct Semantics (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-direct-semantics/
[24] W3C. OWL Web Ontology Language Manchester Syntax (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[25] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax (Second Edition). W3C (2012). URL: http://www.w3.org/TR/owl2-syntax/
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules