Verbalizing Business Rules (Part 6)
Business rules should be validated by business domain experts, and hence specified using concepts and languages easily understood by business people. This is the sixth in a series of articles on expressing business rules formally in a high-level, textual language. This article considers verbalization of value constraints.
The first article[3] discussed criteria for a business rules language, and verbalization of simple uniqueness and mandatory constraints on binary associations. The second article[4] examined hyphen-binding, and verbalization of internal uniqueness constraints that span a whole association, or that apply to n-ary associations. The third article[5] covered verbalization of basic external uniqueness constraints. The fourth article[6] considered relational-style verbalization of external uniqueness constraints involving nesting or long join paths, as well as attribute-style verbalization of uniqueness constraints and simple mandatory constraints. The fifth article[7] discussed verbalization of mandatory constraints on roles of n-ary associations, and disjunctive mandatory constraints (also known as inclusive-or constraints) over sets of roles.
Verbalization of value constraints
For our purposes, a value as either a lexical constant such as a character string (e.g., 'Australia') or a number that is referenced using Hindu-Arabic notation (e.g., the number 'ten' depicted by the numeral '10'). A value type is a named set of possible values. In Object-Role Modeling (ORM), a value constraint may be used to declare the possible extension of a value type. When depicted graphically, an ORM value constraint is placed next to the object type it constrains, using braces to enclose the set of possible values.
If an entity type (non-lexical type) has a preferred identification scheme that maps the entity type to a value type, a value constraint may be applied to the entity type with the understanding that it strictly applies to the underlying value type. For example, if each gender is identified by a gender code whose possible values are 'M' (for male) and 'F' (for female), this may be depicted compactly as in Figure 1(a), which is taken to be an abbreviation of the explicit representation in Figure 1(b). If desired, the explicit representation may be used instead.
When value constraints are declared in full by listing each possible value, as in Figure 1, this is called an enumeration. In UML, enumeration types may be modeled as classes, stereotyped as enumerations, with their values listed as attributes, as in Figure 1(c).
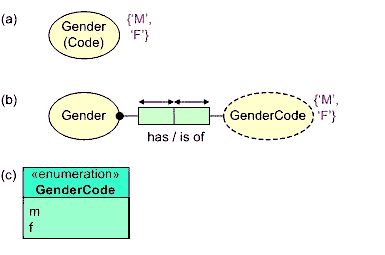
Figure 1. A value constraint may be used to enumerate the possible values for an object type.
Value constraints expressed as an enumeration of a value type A{a1, …, an} may be verbalized using the pattern: The possible values of A are a1, …, an. When applied to an entity type, the preferred reference mode should be included to avoid any chance of misinterpretation. For example,
The possible values of Gender(Code) are 'M', 'F'.
or alternatively
The possible values of GenderCode are 'M', 'F'.
If the values comprise a list of consecutive values, with a predefined ordering, they may be declared simply as a range with a start and end value. Figure 2 shows a simple example in both ORM and UML notations. As discussed in earlier articles, our use of '{P}' to denote the preferred reference scheme for papers is a not part of standard UML. In the UML example, we have chosen to model the 'rating' fact type using an attribute. Although we could have used an enumeration type with the values 1, 2, 3, 4, 5, 6, 7, the use of enumeration types becomes impractical if the ranges are large (e.g., 1..1000, or even 1..100). Here the constraint on rating is depicted with a textual constraint using the UML braces notation. In this case, the value constraint applies only to the 'rating' attribute, so if other attributes are based on the same domain the constraint needs to be repeated for each attribute.
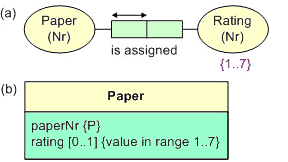
Figure 2. A value constraint expressed as a range in (a) ORM and (b) UML.
Value constraints expressed as a single range A{a1 .. an} may be verbalized using the pattern: The possible values of A are a1 .. an. The word 'to' may be used in place of '..'. Again, reference modes should be included if the constraint is specified on an entity type. For example, for the 'Rating' object type in Figure 2(a) the value constraint may be declared using any of the following:
The possible values of Rating(Nr) are 1..7.
The possible values of Rating(Nr) are 1 to 7.
The possible values of RatingNr are 1..7.
The possible values of RatingNr are 1 to 7.
and for the 'rating' attribute in Figure 2(b) we may declare
The possible values of Paper.rating are 1..7.
Numeric ranges with a lower bound of n but with no upper bound may be declared using the phrase 'greater than or equal to n', or 'at least n' or 'n or more'. Numeric ranges with an upper bound of n but with no lower bound may be declared using the phrase 'less than or equal to n', 'at most n' or 'up to n'. Figure 3 shows two simple examples.

Figure 3. It is possible that a value range is bounded at one end only.
The constraint in Figure 3(a) may be verbalized using any of the following:
The possible values of WholeNumber are greater than or equal to 0.
The possible values of WholeNumber are 0 or more.
Each WholeNumber has a value of at least 0.
The constraint in Figure 3(b) may be verbalized using any of the following:
The possible values of NegativeInteger are less than or equal to -1.
The possible values of NegativeInteger are up to -1.
Each NegativeInteger has a value of at most -1.
Note that the above constraints do not by themselves formally
restrict the instances of 'WholeNumber' or 'NegativeInteger' to integers, even though
the names of the types informally suggest this. To add this restriction to
integers, we need to either associate the types with an integer data type, or define
them explicitly as subtypes of an integer type. For example, if you are using
Microsoft Visio for Enterprise Architects™ to enter a value constraint, you should
also choose an appropriate data type for the object type.[8]
A single value constraint may also combine multiple enumerations and/or ranges. Two examples taken from [1] are shown in Figure 4. These may be verbalized as shown below. If desired, 'to' may be used instead of '..'. Notice the importance of including the reference mode (Celsius) for temperature, to avoid users applying this constraint in a different temperature scale (e.g., Fahrenheit or Kelvin).
The possible values of ExtremeTemperature(Celsius) are -100..-20,40..100.
The possible values of SQLcharacter are 'a'..'z', 'A'..'Z', '0'..'9', '_'.
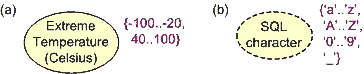
Figure 4. A value constraint may include multiple enumerations and ranges.
The value constraints considered so far correspond to a set of one or more value sets, each of which may be specified either as a set of values or as a range with a smallest value and/or a largest value. In rare cases we may wish to constrain values to a set that requires other kinds of expression. For example, let us use 'PositiveReal' to name the set of positive real numbers. We cannot specify a minimum value for this type, but we may define the type to be a real number that is greater than 0, using the same mechanism used for defining subtypes (see later article).
As another example, we mighty require that 'CommitteeSize' must map to an odd number. To specify this formally, it is useful to have relevant built-in numeric operations or functions. For example, the Object Constraint Language (OCL)[10] includes the modulo operation, which may be used to determine whether an integer x is odd (x is odd if and only if x mod 2 returns 1). Of course, any constraint may also be specified informally.
In ORM models, it is sometimes useful to specify a value constraint on a role rather than an object type. Although such constraints may be captured by applying value constraints to subtypes, it is often more convenient to apply value constraints to roles without explicitly introducing subtypes. Figure 5(a) shows two examples of such a role-value constraint, taken from one of my metamodels for information engineering.[2] While the object type 'Multiplicity' has three possible values, only two of these are available for the minimum multiplicity role, with a different value pair available for the maximum multiplicity role. Figure 5(b) shows a corresponding UML model, using a textual constraint for each of the 'multiplicity' attributes. These value constraints may be verbalized thus:
For each Role that has a minimum Multiplicitythe possible values of minMultiplicity(Code) are '0', '1'.For each Role that has a maximum Multiplicitythe possible values of maxMultiplicity(Code) are '1', 'n'.
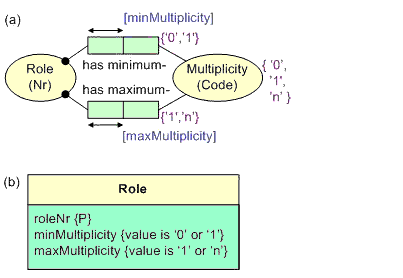
Figure 5. Role-value constraint in ORM is equivalent to an attribute-value constraint in UML.
The verbose verbalization above caters for the case where the mandatory constraints might not apply. If 'value' is understood to mean existing value (non-null), then a compact attribute-style verbalization may be used. For example,
The possible values of Role.minMultiplicity are '0', '1'.
Although role-value constraints have been used in ORM for some time, current ORM tools typically do not yet support their graphical declaration, restricting their coverage of value constraints to object types.
That completes our coverage of value constraints and their verbalization. The next article considers subset constraints.
References
[1] T.A. Halpin. Information Modeling and Relational
Databases. Morgan Kaufmann, San Francisco, 2001. ![]()
[2] T.A. Halpin. "Metaschemas for ER, ORM and
UML Data Models: A Comparison," Journal of Database Management,
Vol. 13, No. 2 (2002), pp. 20-29. Idea Publishing Group, Hershey, PA, USA. ![]()
[3] T.A. Halpin. "Verbalizing Business Rules
(part 1)," Business Rules Journal, Vol. 4, No. 4 (April 2003).
URL: http://www.BRCommunity.com/a2003/b138.html ![]()
[4] T.A. Halpin. "Verbalizing Business Rules
(part 2)," Business Rules Journal, Vol. 4, No. 6 (June 2003). URL: http://www.BRCommunity.com/a2003/b152.html ![]()
[5] T.A. Halpin. "Verbalizing Business Rules
(part 3)," Business Rules Journal, Vol. 4, No. 8 (August 2003).
URL: http://www.BRCommunity.com/a2003/b163.html ![]()
[6] T.A. Halpin. "Verbalizing Business Rules
(part 4)," Business Rules Journal, Vol. 4, No. 10 (October 2003).
URL: http://www.BRCommunity.com/a2003/b172.html ![]()
[7] T.A. Halpin. "Verbalizing Business Rules
(part 5)," Business Rules Journal, Vol. 5, No. 2 (February 2004).
URL: http://www.BRCommunity.com/a2003/b179.html ![]()
[8] T.A. Halpin, K. Evans, P. Hallock, & B. MacLean.
Database Modeling with Microsoft Visio for Enterprise Architects. Morgan
Kaufmann, San Francisco, 2003. ![]()
[9] Object Management Group. UML 2.0 Infrastructure. Object Management Group, 2003. URL: http://www.omg.org/uml
[10] Object Management Group. UML 2.0 Object
Constraint Language. Object Management Group, 2003. URL: http://www.omg.org/uml ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules