This is the eleventh article in a series on logic-based approaches to data modeling.  The first article^[A] briefly overviewed deductive databases and illustrated how simple data models with asserted and derived facts may be declared and queried in LogiQL^{[2], [8], [10]} a leading-edge deductive database language based on extended datalog.^[1]  The second article^[B] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL.  The third article^[C] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.  The fourth article^[D] discussed how to declare external uniqueness constraints. 

The fifth article^[E] covered derivation rules in a little more detail and showed how to declare inclusive-or constraints.  The sixth article^[F] discussed how to declare simple set-comparison constraints (i.e., subset, exclusion, and equality constraints) and exclusive-or constraints.  The seventh article^[G] explained how to declare subset, constraints between compound role sequences, including cases involving join paths.  The eighth article^[H] discussed how to declare exclusion and equality constraints between compound role sequences.  The ninth article^[I] explained how to declare basic subtyping in LogiQL.  The tenth article^[J] discussed how to declare relationships to be irreflexive (using a ring constraint) and/or symmetric (using a ring constraint or a derivation rule) in LogiQL.

The current article shows how to constrain a relationship to be asymmetric and/or intransitive.  The LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.

A Parenthood Chart from Egyptian Mythology

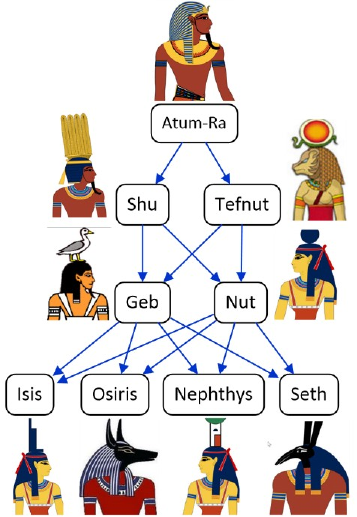
Figure 1 pictures the nine Egyptian gods collectively known as the Great Ennead of Heliopolis.  Each god is identified by its name and is a parent of zero or more gods in the same Ennead.   A downwards arrow depicts the parent to child relationship.  A similar example was discussed in a previous article^[C] to illustrate some basic derivation rules but wrongly included Horus (a son of Isis and Osiris) as part of the Ennead.

Figure 1.  Parenthood relationships of the Great Ennead of Heliopolis.

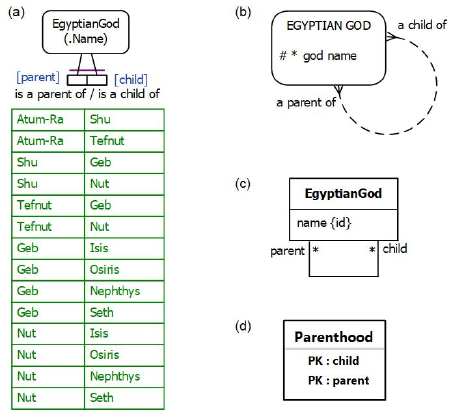
Figure 2(a) provides a simplified data model for this example using a populated Object-Role Modeling (ORM)^{[5], [6], [7]} diagram, showing both a forward predicate reading ("is a parent of") and an inverse predicate reading ("is a child of") for the parenthood relationship.  Role names ("parent", "child") for the parenthood relationship are also provided.  The example is schematized in Figure 2(b) as an Entity Relationship diagram in Barker notation (Barker ER),^[3] in Figure 2(c) as a class diagram in the Unified Modeling Language (UML),^[11] and in Figure 2(d) as a relational database (RDB) schema.

Figure 2.  Simplified data model for Figure 1 in (a) ORM, (b) Barker ER, (c) UML, and (d) RDB notation.

In the ORM schema in Figure 2(a), the preferred reference scheme for EgyptianGod is depicted by the popular reference mode "Name" shown in parentheses.  The spanning uniqueness constraint over the parenthood fact type (shown as a bar over the constrained roles) indicates that the relationship is many-to-many.  The absence of a mandatory role dot on the roles indicates that each role in the parenthood fact type is optional.

The Barker ER schema in Figure 2(b) depicts the primary reference scheme for EgyptianGod by prepending an octothorpe "#" to the god name attribute, with an asterisk "*" to indicate the attribute is mandatory.  The many-to-many nature of the parenthood relationship is depicted by a crowsfoot at each end, and the optionality of the roles is indicated by using a dashed line for the relationship.

The UML class diagram in Figure 2(c) depicts the primary identification for EgyptianGod by appending "{id}" to the name attribute.  The multiplicity constraints shown as a star ("*") at both ends of the parenthood association indicates the optional, many-to-many nature of the association.

Figure 2(d) shows the relational database schema diagram generated by the NORMA tool^[4] from the ORM schema.  Here, prepending "PK" to the child and parent attributes indicates that their combination provides the primary key of the table and hence each (parent, child) entry is unique.

The previous article^[J] discussed how to declare irreflexive ring constraints.  The parenthood relation is clearly irreflexive since no Egyptian god can be a parent of itself.  However, as discussed in the next section, the parenthood relation is also asymmetric, and since asymmetry implies irreflexivity there is no need to declare irreflexivity if asymmetry has already been declared.

In this article the Ennead parenthood example is used to illustrate how asymmetric and intransitive ring constraints may be specified in ORM and coded in LogiQL.  However, as discussed in later articles, a complete data model for this example involves recursive ring constraints (strongly intransitive and acyclic constraints) as well as a frequency constraint.

As Barker ER, UML, and RDB notations have no graphic way to depict ring constraints at all, those alternative modeling notations will be ignored for the rest of this article.

Asymmetric and Intransitive Ring Constraints

The ORM binary fact type EgyptianGod is a parent of Egyptian God in Figure 2(a) is a ring fact type.  As most easily seen from the parenthood chart in Figure 1, if one Egyptian god in the Ennead is a parent of another in the Ennead, then the other (the child) cannot be a parent of its parent (the parenthood arrows are directed down but not up).  In general, a binary predicate R is asymmetric if and only if, given any objects x and y, if xRy then it cannot be that yRx.   In other words, asymmetric relationships work in one direction only.

The alphabetical precedence constraint in the Country preborders Country example from the previous article^[J] implies that the preborders predicate is asymmetric (if x < y then it cannot be that y < x), so there is no need to explicitly add an asymmetry constraint for that example.   For the parenthood relationship in Figure 2(a), however, an asymmetric constraint needs to be explicitly declared.  In ORM this is done by attaching an asymmetric ring constraint shape to the pair of constrained roles.  If the roles are contiguous, the constraint is attached to the junction of the two role boxes.

The top part of Figure 3(a) displays an intuitive shape for asymmetry, and the lower part shows the simpler, asymmetric constraint shape actually used in ORM.  The black shape at the top of Figure 3(a) suggests asymmetry by using a dot for an object, a directed arrow for the relationship from left to right, and a stroke to indicate that the righthand object cannot relate to the lefthand object via this relationship.  The violet shape below this is the actual shape used in ORM to depict asymmetry.  The removal of the arrow-tip enables use of a smaller shape that can still be easily distinguished from other shapes.

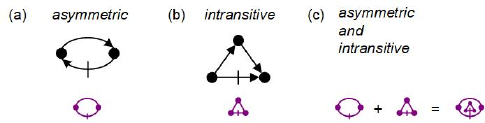
Figure 3.  ORM graphical notation for asymmetric and intransitive ring constraints.

As most easily seen from the Ennead parenthood chart in Figure 1, if one Egyptian god is a parent of second Egyptian god who is parent of a third Egyptian god, then the first Egyptian god cannot be a parent of the third Egyptian god (i.e., no incest with one's child occurs).  Visually, no parenthood arrow goes from a god to a grandchild of that god.  In general, a binary predicate R is intransitive if and only if, given any objects x, y, and z, if xRy and yRz then it cannot be that xRz.  Hence, the Ennead parenthood relationship is intransitive, and we need to add an intransitive ring constraint to ensure this.

The top part of Figure 3(b) displays an intuitive shape for intransitivity, and the lower part shows the simpler, intransitive constraint shape actually used in ORM.  When both constraints apply, as in this parenthood example, a composite constraint shape is used that overlays the two shapes, as shown in Figure 3(c).

Figure 4 shows the ORM schema for the Ennead parenthood relationship with the combined shape for the asymmetric and intransitive ring constraints connected by a dashed line to the junction of the two roles in the relationship.

Figure 4.  Adding asymmetric and intransitive ring constraints to the Ennead parenthood relationship.

For this example, the NORMA tool^[4] automatically verbalizes the asymmetric constraint as:

If EgyptianGod₁ is a parent of EgyptianGod₂
then it is impossible that EgyptianGod₂ is a parent of EgyptianGod₁.

The intransitivity constraint verbalizes thus:

If EgyptianGod₁ is a parent of EgyptianGod₂ and EgyptianGod₂ is a parent of EgyptianGod₃
then it is impossible that EgyptianGod₁ is a parent of EgyptianGod₃.

Coding the Model in LogiQL

The ORM schema in Figure 4 may be coded in LogiQL as shown below.  The right arrow symbol "->" stands for the material implication operator "→" of logic and is read as "implies."  The left arrow symbol "<-" stands for the inverse material implication operator "←" of logic and is read as "if."  An exclamation mark "!" denotes the logical negation operator and is read as "it is not the case that."  A comma "," denotes the logical conjunction operator "&", and is read as "and."  LogiQL is case-sensitive; each formula must end with a period, and head variables are implicitly universally quantified.

The first line declares EgyptianGod as an entity type whose instances are referenced by god names that are coded as character strings.  The colon ":" in hasGodName(g:gn) distinguishes hasGodName as a refmode predicate, so this predicate is injective (mandatory, 1:1).  The second line declares the typing constraints on the isaParentOf predicate.  Comments are prepended by "//".  The third line is a derivation rule to declare the isaChildOf predicate as the inverse of the isaParentOf predicate.

The fourth line declares the asymmetric ring constraint and corresponds to the logical formula
    ∀g1,g2 (g1 isaParentof g2 →  ~ g2 isaParentof g1)

The fifth line declares the intransitive ring constraint, and corresponds to the logical formula
    ∀g1,g2,g3(g1 isaParentof g2 & g2 isaParentof g3 →  ~ g1 isaParentof g3)

EgyptianGod(g), hasGodName(g:gn)  ->  string(gn).
isaParentOf(g1, g2)  ->  EgyptianGod(g1), EgyptianGod(g2).
isaChildOf(g1, g2)  <-  isaParentOf(g2, g1).
isaParentOf(g1, g2) -> !isaParentOf(g2, g1).  // asymmetric
isaParentOf(g1, g2), isaParentOf(g2, g3) ->  !isaParentOf(g1, g3).  // intransitive

To enter the schema in the free, cloud-based REPL tool, use a supported browser to access the website https://repl.logicblox.com.  Alternatively, you can access https://developer.logicblox.com/playground/ then click the "Open in new window" link to show a full screen for entering the code.

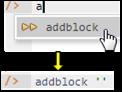
Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block.  After the "/>" prompt, type the letter "a", and click the addblock option that then appears.  This causes the addblock command (followed by a space) to be added to the code window.  Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes, ready for your block of code (see Figure 5).

Figure 5.  Invoking the addblock command in the REPL tool.

Now copy the schema code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 6).  By default, the REPL tool also appends an automatically-generated identifier for the code block.  Alternatively, you can enter each line of code directly, using a separate addblock command for each line.

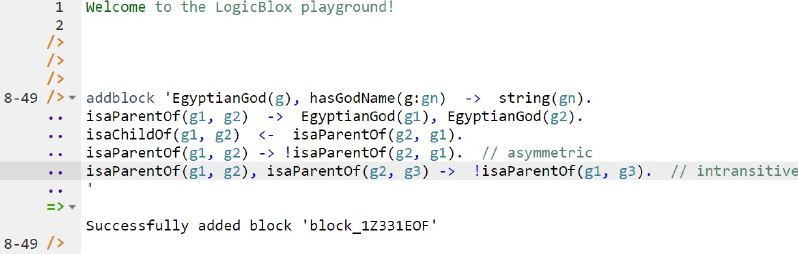
Figure 6.  Adding a block of schema code.

The data in Figure 2(a) may be entered in LogiQL using the following delta rules.  A delta rule of the form +fact inserts that fact.  Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes.  Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.

+EgyptianGod(g1), +hasGodName(g1:"Atum-Ra"), +EgyptianGod(g2), +hasGodName(g2:"Shu"),
+EgyptianGod(g3), +hasGodName(g3:"Tefnut"), +EgyptianGod(g4), +hasGodName(g4:"Geb"),
+EgyptianGod(g5), +hasGodName(g5:"Nut"), +EgyptianGod(g6), +hasGodName(g6:"Isis"),
+EgyptianGod(g7), +hasGodName(g7:"Osiris"), +EgyptianGod(g8), +hasGodName(g8:"Nephthys"),
+EgyptianGod(g9), +hasGodName(g9:"Seth"),
+isaParentOf(g1, g2), +isaParentOf(g1, g3),
+isaParentOf(g2, g4), +isaParentOf(g2, g5),
+isaParentOf(g3, g4), +isaParentOf(g3, g5),
+isaParentOf(g4, g6), +isaParentOf(g4, g7), +isaParentOf(g4, g8), +isaParentOf(g4, g9),
+isaParentOf(g5, g6), +isaParentOf(g5, g7), +isaParentOf(g5, g8), +isaParentOf(g5, g9).

Delta rules to add or modify data are entered using the exec (for 'execute') command.  To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list.  A space character is automatically appended.  Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules.  Now copy the lines of data code provided above to the clipboard (e.g. using Ctrl+C), then paste it between the quotes (e.g. using Ctrl+V), and then press the Enter key.  A new prompt awaits your next command (see Figure 7).

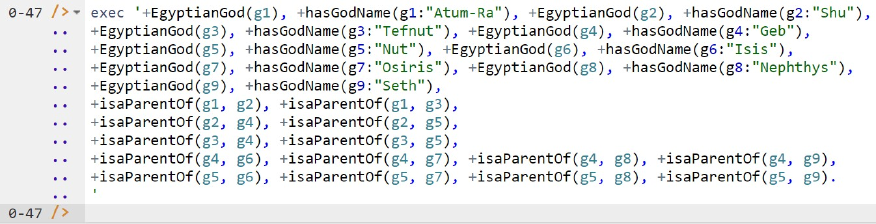
Figure 7.  Adding the data.

Now that the data model (schema plus data) is stored, you can use the print command to inspect the contents of any predicate.  For example, to list the names of all the nine Ennead gods, type "p" then select print from the drop-down list, then type a space followed by "E", then select EgyptianGod from the drop-down list and press Enter.  Alternatively, type "print EgyptianGod" yourself and press Enter.

Figure 8 shows the result (after scrolling down, as by default the REPL tool displays at most 6 rows at a time).

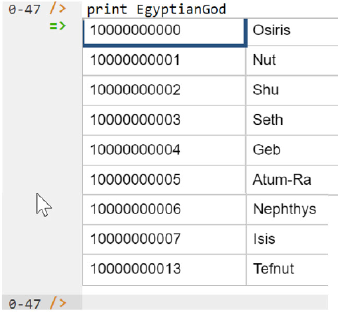
Figure 8.  Using the print command to list the Ennead gods.

By default, the REPL tool prepends a column listing automatically-generated, internal identifiers for the returned entities.  Similarly, you can use the print command to print the extension of the other predicates.

As discussed in previous articles, to perform a query, you specify a derivation rule to compute the facts requested by the query.  For example, the following query may be used to list the names of the Ennead gods who have Geb as a parent.  The rule's head uses an anonymous predicate to capture the result derived from the rule's body.  The head variable gn is implicitly universally quantified.  The variables g1 and g2 introduced in the rule body are implicitly existentially quantified.

_(gn) <- hasGodName(g1:"Geb"), isaParentOf(g1, g2), hasGodName(g2:gn).

In LogiQL, queries are executed by appending their code in single quotes to the query command.  To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter.  The relevant query result is now displayed as shown in Figure 9.

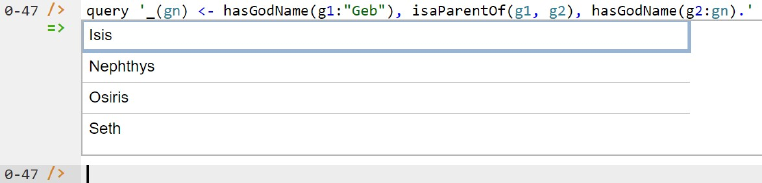
Figure 9.  A query to list the names of those Ennead gods with Geb as a parent.

Conclusion

The current article discussed how to constrain relationships to be asymmetric and intransitive in ORM and LogiQL.  The next few articles will develop the Ennead example further, adding two recursive ring constraints (acyclic and strongly intransitive constraints) that imply the two ring constraints discussed in this article, as well as adding a frequency constraint.  The core reference manual for LogiQL is accessible at https://developer.logicblox.com/content/docs4/core-reference/.  An introductory tutorial for LogiQL and the REPL tool is available at https://developer.logicblox.com/content/docs4/tutorial/repl/section/split.html.  Further coverage of LogiQL may be found in [8].

References

[1]  S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995).  

[2]  M. Aref, B. Cate, T. Green, B. Kimefeld, D. Olteanu, E. Pasalic, T. Veldhuizen, & G. Washburn, "Design and Implementation of the LogicBlox System," Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York (2015).  http://dx.doi.org/10.1145/2723372.2742796  

[3]  R. Barker, CASE*Method:  Entity Relationship Modelling, Addison-Wesley:  Wokingham, England (1990).  

[4]  M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2," P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204.  

[5]  T.A. Halpin, Object-Role Modeling Fundamentals, Technics Publications:  New Jersey (2015).  

[6]  T.A. Halpin, Object-Role Modeling Workbook, Technics Publications:  New Jersey (2016).  

[7]  T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann:  San Francisco (2008).  

[8]  T.A. Halpin & S. Rugaber, LogiQL:  A Query language for Smart Databases, CRC Press:  Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939#  

[9]  T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.  

[10]  S. Huang, T. Green, & B. Loo, "Datalog and emerging applications:  an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011).  At:  http://dl.acm.org/citation.cfm?id=1989456  

[11]  Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013).  Available online at:  http://www.omg.org/spec/UML/2.5/Beta2/  

[12]  Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1, Object Management Group (2012).  Retrieved from http://www.omg.org/spec/OCL/2.3.1/  

Earlier Parts in this Series

[A]  T.A. Halpin, "Logical Data Modeling (Part 1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL:  http://www.BRCommunity.com/a2014/b760.html  

[B]  T.A. Halpin, "Logical Data Modeling (Part 2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL:  http://www.BRCommunity.com/a2014/b780.html  

[C]  T.A. Halpin, "Logical Data Modeling (Part 3)," Business Rules Journal, Vol. 16, No. 1 (Jan. 2015), URL:  http://www.BRCommunity.com/a2015/b795.html  

[D]  T.A. Halpin, "Logical Data Modeling (Part 4)," Business Rules Journal, Vol. 16, No. 7 (July 2015), URL:  http://www.BRCommunity.com/a2015/b820.html  

[E]  T.A. Halpin, "Logical Data Modeling (Part 5)," Business Rules Journal, Vol. 16, No. 10 (Oct. 2015), URL:  http://www.BRCommunity.com/a2015/b832.html  

[F]  T.A. Halpin, "Logical Data Modeling (Part 6)," Business Rules Journal, Vol. 17, No. 3 (Mar. 2016), URL:  http://www.BRCommunity.com/a2016/b852.html  

[G]  T.A. Halpin, "Logical Data Modeling (Part 7)," Business Rules Journal, Vol. 17, No. 7 (July 2016), URL:  http://www.BRCommunity.com/a2016/b866.html  

[H]  T.A. Halpin, "Logical Data Modeling (Part 8)," Business Rules Journal, Vol. 17, No. 11 (Nov. 2016), URL:  http://www.BRCommunity.com/a2016/b883.html  

[I]  T.A. Halpin, "Logical Data Modeling (Part 9)," Business Rules Journal, Vol. 18, No. 5 (May 2017), URL:  http://www.BRCommunity.com/a2017/b906.html  

[J]  T.A. Halpin, "Logical Data Modeling (Part 10)," Business Rules Journal, Vol. 18, No. 11 (Nov. 2017), URL:  http://www.BRCommunity.com/a2017/b929.html  

# # #