This is the twelfth article in a series on logic-based approaches to data modeling.  The first article^[A] briefly overviewed deductive databases and illustrated how simple data models with asserted and derived facts may be declared and queried in LogiQL^{[2], [8], [10]} a leading-edge deductive database language based on extended datalog.^[1]  The second article^[B] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL.  The third article^[C] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.  The fourth article^[D] discussed how to declare external uniqueness constraints.  The fifth article^[E] covered derivation rules in a little more detail and showed how to declare inclusive-or constraints.  The sixth article^[F] discussed how to declare simple set-comparison constraints (i.e., subset, exclusion, and equality constraints) and exclusive-or constraints.  The seventh article^[G] explained how to declare subset, constraints between compound role sequences, including cases involving join paths.  The eighth article^[H] discussed how to declare exclusion and equality constraints between compound role sequences.  The ninth article^[I] explained how to declare basic subtyping in LogiQL.  The tenth article^[J] discussed how to declare relationships to be irreflexive (using a ring constraint) and/or symmetric (using a ring constraint or a derivation rule) in LogiQL.  The eleventh article^[K] showed how to constrain a relationship to be asymmetric and/or intransitive.

The current article discusses how to declare recursive derivation rules in LogiQL and how to constrain ring relationships to be acyclic and/or strongly.  The LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.

A Parenthood Chart from Egyptian Mythology

Figure 1 pictures the nine Egyptian gods collectively known as the Great Ennead of Heliopolis.  Each god is identified by its name and is a parent of zero or more gods in the same Ennead.  A downwards arrow depicts the parent to child relationship.  This example was discussed in the previous article^[K] to illustrate asymmetric and intransitive ring constraints.

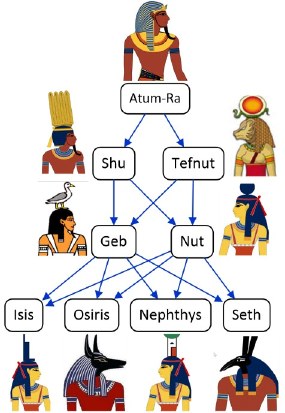
Figure 1.  Parenthood relationships of the Great Ennead of Heliopolis.

Figure 2(a) provides a simplified data model for this example using a populated Object-Role Modeling (ORM)^{[5], [6], [7]} diagram, with the parenthood relationship constrained to be asymmetric and intransitive.  The example is schematized in Figure 2(b) as an Entity Relationship diagram in Barker notation (Barker ER),^[3] in Figure 2(c) as a class diagram in the Unified Modeling Language (UML),^[11] and in Figure 2 d) as a relational database (RDB) schema.  For detailed discussion of these schemas see the previous article.^[K]  The UML, Barker ER, and RDB schemas have no graphical way to depict ORM ring constraints, so are ignored in the rest of this article.

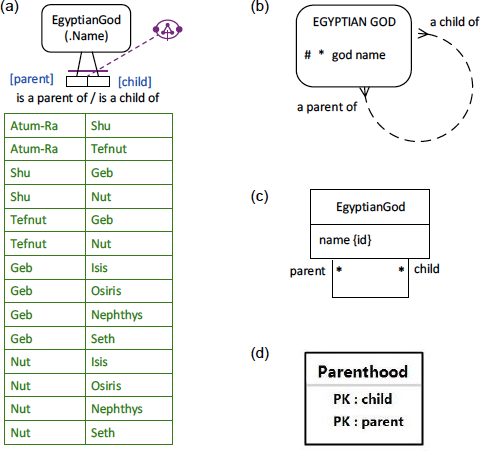
Figure 2.  Simplified data model for Figure 1 in (a) ORM, (b) Barker ER, (c) UML, and (d) RDB notation.

A complete data model for this example involves recursive ring constraints (acyclic and strongly intransitive constraints) as well as a frequency constraint.  This article discusses how to specify recursive derivation rules in ORM and LogiQL, and how to add acyclic and strongly intransitive constraints to the parenthood relationship.

Recursive Derivation Rules

A derivation rule includes a head (what is derived) as well as a body (what is used to make the derivation).  A derivation rule is recursive if its head includes a predicate that is also used in its body.  For example, the ORM schema in Figure 3 extends our earlier ORM schema about the Great Ennead by adding the derived fact type EgyptianGod is an ancestor of EgyptianGod and a recursive derivation rule for the ancestorhood fact type (the head of the rule).  Derived fact types and derivation rules are marked with an asterisk "*".

Figure 3.  An ORM schema where ancestorhood is derived using a recursive derivation rule.

The ORM derivation rule is expressed textually in FORML (Formal ORM Language), using subscripted, typed variables.  Logical words are shown in bold type.  Here "iff" is shorthand for "if and only if".  As in LogiQL, head variables are assumed to be universally quantified, with variables introduced in the body existentially quantified.  The use of pronouns such as "who" or "that" enables variable binding to be expressed naturally.  The logical inclusive-disjunction operator is denoted by "or".

Given the population of the parenthood relation shown in Figure 1 and Figure 2(a), the derivation rule determines the population of the ancestorhood fact type.  Atum-Ra is an ancestor of the other seven gods; Shu and Tefnut are each an ancestor of six gods (Geb, Nut, Isis, Osiris, Nepthys, and Seth); Geb and Nut are each an ancestor of four gods (Isis, Osiris, Nepthys, and Seth).  So the fact table for the fact type EgyptianGod is an ancestor of EgyptianGod has 27 fact instances.  The ancestorhood relation is the transitive closure of the parenthood relation.

As discussed in the previous article, the asserted aspects of the ORM schema in Figure 2(a) may be coded in LogiQL as shown below.

EgyptianGod(g), hasGodName(g:gn)  ->  string(gn).
isaParentOf(g1, g2)  ->  EgyptianGod(g1), EgyptianGod(g2).
isaChildOf(g1, g2)  <-  isaParentOf(g2, g1).
isaParentOf(g1, g2) -> !isaParentOf(g2, g1).  // asymmetric
isaParentOf(g1, g2), isaParentOf(g2, g3) ->  !isaParentOf(g1, g3).  // intransitive

The derivation rule for ancestorhood may be coded in LogiQL as shown below.  The left-arrow symbol "<-" denotes the inverse material implication operator "←" of logic, and is read as "if".  LogiQL adopts the closed world assumption, so if no other rules with the same head are present in the global schema the "if" operator may be interpreted as "iff".  LogiQL uses a comma "," for the logical conjunction operator "&" (read as "and") and a semicolon ";" for the inclusive disjunction operator "∨" (read as "or").  The LogiQL code is equivalent to the logical formula
  ∀g1 ∀g2 [g1 isanAncestorOf g2 ← (g1 isaParentOf g2 ∨ ∃g3(g1 isaParentOf g3 & g3 isanAncestorOf g2))].

isanAncestorOf(g1, g2)  <- 
    isaParentOf(g1, g2) ;
    isaParentOf(g1, g3), isanAncestorOf(g3, g2).

Acyclic and Strongly Intransitive Ring Constraints

In the parenthood graph in Figure 1 the arrows representing the "is a parent of" relationship always point downwards, never upwards; so there are no cycles in this graph (i.e., the graph is acyclic).  If we ignore reincarnation, the "is a parent of" relationship is acyclic for people and other animals in general, not just for the Egyptian gods in the Great Ennead of Heliopolis.  So nobody is a parent of itself, or a grandparent of itself, or a great grandparent of itself, and so on.

In general, a ring relationship R is acyclic if and only if no object may cycle back to itself by applying R one or more times.  Figure 4(a) intuitively depicts the three simplest cases (where the relationship R is applied once, twice, or three times), using dots for objects, arrows for instances of the R relation, and a stroke through an arrow to indicate an impossibility.  Figure 4(b) depicts the ORM constraint shape for acyclicity, which is a simplified version of the third case, with arrow-tips removed.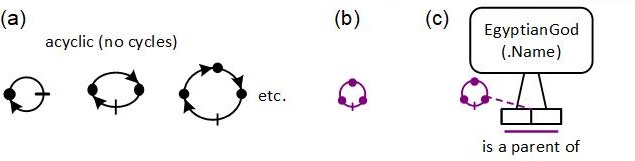

Figure 4.  (a) Motivation for (b) ORM's graphical notation for an acyclic ring constraint, and (c) an example.

Figure 4 (c) adds an acyclic ring constraint in the "is a parent of" relationship.  Connecting the constraint shape to the join of the two roles in the fact type indicates that the constraint applies to the role-pair.  The NORMA tool for ORM^[4] verbalizes this constraint as follows: 
     No EgyptianGod may cycle back to itself via one or more applications of EgyptianGod is a parent of EgyptianGod.

Since there is no restriction on how long a cycle may be, acyclicity constraints are naturally enforced using recursion.  If there were a cycle in the parenthood graph, it would mean that somebody is an ancestor of himself/herself.  Hence we can implement acyclicity on parenthood by constraining ancestorhood to be irreflexive.  In LogiQL, if the isanAncestorOf predicate is recursively derived as given earlier, this irreflexive constraint may be coded as shown below.  Recall that LogiQL uses an exclamation mark "!" for the logical negation operator "~" (read as "it is not the case that").  In general, any binary predicate may be constrained to be acyclic by deriving a predicate to produce its transitive closure and constraining that predicate to be irreflexive.

!isanAncestorOf(g, g).    // No Egyptian God is an ancestor of itself

As discussed in the previous article^[K] the parenthood relation under discussion is intransitive.  The NORMA tool verbalizes this intransitive ring constraint thus:
    If EgyptianGod₁ is a parent of EgyptianGod₂ and EgyptianGod₂ is a parent of EgyptianGod₃ then it is impossible that EgyptianGod₁ is a parent of EgyptianGod₃.
However, the parenthood predicate for the Great Ennead is not just intransitive, but strongly intransitive, so no Egyptian god can be a parent of any of his/her descendants that are not one of his/her children.  While incest between siblings may occur between the Egyptian Gods (Figure 1 includes several examples), incest with one's descendant(s) does not.

The ORM constraint shape for strong intransitivity adds an extra dot to the simple intransitivity constraint shape, as shown in Figure 5(a).  NORMA verbalizes this constraint thus:
    If EgyptianGod₁ is a parent of some EgyptianGod₂ then EgyptianGod₁cannot be indirectly related to EgyptianGod₃ by multiple applications of this relationship.
Figure 5(b) depicts the parenthood fact type with both strongly intransitive and acyclic ring constraints added.  For compact display when both constraints apply, a composite constraint shape is used that overlays the two shapes, as shown in Figure 5(c).

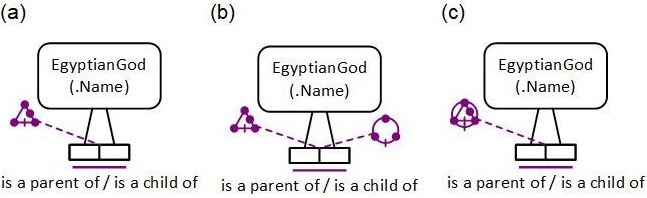
Figure 5.  Adding a strongly intransitive ring constraint to the Ennead parenthood relationship.

The strong intransitivity constraint may be coded in LogiQL as shown below.  Note that acyclicity implies asymmetry, and strong intransitivity implies simple intransitivity, so there is no longer a need to include those weaker ring constraints discussed in the previous article.

// No EgyptianGod is a parent of a descendant of one of its children
isaParentOf(g1, g2), isanAncestorOf(g2, g3)  ->  !isaParentOf(g1, g3).

Coding the Model in LogiQL

The ORM schema in Figure 5(c) may be coded in LogiQL as shown below.

EgyptianGod(g), hasGodName(g:gn)  ->  string(gn).
isaParentOf(g1, g2)  ->  EgyptianGod(g1), EgyptianGod(g2).
isaChildOf(g1, g2)  <-  isaParentOf(g2, g1).
isaParentOf(g1, g2) -> !isaParentOf(g2, g1).  // asymmetric
isaParentOf(g1, g2), isaParentOf(g2, g3) ->  !isaParentOf(g1, g3).  // intransitive
isanAncestorOf(g1, g2)  <- 
         isaParentOf(g1, g2) ;
         isaParentOf(g1, g3), isanAncestorOf(g3, g2).
!isanAncestorOf(g, g). // No Egyptian God is an ancestor of itself
// No EgyptianGod is a parent of a descendant of one of its children
isaParentOf(g1, g2), isanAncestorOf(g2, g3)  ->  !isaParentOf(g1, g3).

To enter the schema in the free, cloud-based REPL tool, use a supported browser to access the website https://repl.logicblox.com.  Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block.  After the "/>" prompt, type the letter "a", and click the addblock option that then appears.  This causes the addblock command (followed by a space) to be added to the code window.  Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code.

Now copy the schema code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 6).  By default, the REPL tool also appends an automatically generated identifier for the code block.  Alternatively, you can enter each line of code directly, using a separate addblock command for each line.

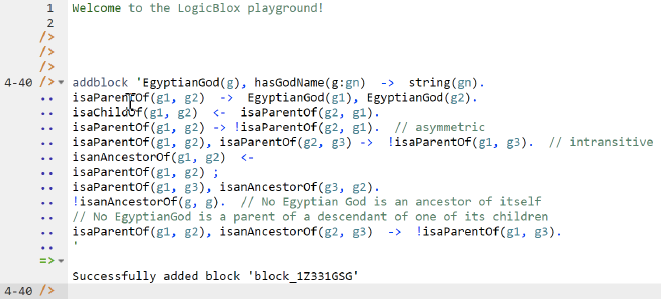
Figure 6.  Adding a block of schema code.

The data in Figure 2(a) may be entered in LogiQL using the following delta rules.  A delta rule of the form +fact inserts that fact.  Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes.  Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.

+EgyptianGod(g1), +hasGodName(g1:"Atum-Ra"), +EgyptianGod(g2), +hasGodName(g2:"Shu"),
+EgyptianGod(g3), +hasGodName(g3:"Tefnut"), +EgyptianGod(g4), +hasGodName(g4:"Geb"),
+EgyptianGod(g5), +hasGodName(g5:"Nut"), +EgyptianGod(g6), +hasGodName(g6:"Isis"),
+EgyptianGod(g7), +hasGodName(g7:"Osiris"), +EgyptianGod(g8), +hasGodName(g8:"Nephthys"),
+EgyptianGod(g9), +hasGodName(g9:"Seth"),
+isaParentOf(g1, g2), +isaParentOf(g1, g3),
+isaParentOf(g2, g4), +isaParentOf(g2, g5),
+isaParentOf(g3, g4), +isaParentOf(g3, g5),
+isaParentOf(g4, g6), +isaParentOf(g4, g7), +isaParentOf(g4, g8), +isaParentOf(g4, g9),
+isaParentOf(g5, g6), +isaParentOf(g5, g7), +isaParentOf(g5, g8), +isaParentOf(g5, g9).

Delta rules to add or modify data are entered using the exec (for 'execute') command.  To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list.  A space character is automatically appended.  Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules.  Now copy the lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  A new prompt awaits your next command (see Figure 7).

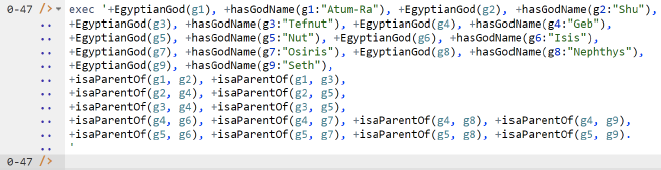
Figure 7.  Adding the data.

Now that the data model is stored, you can use the print command to inspect the contents of any predicate.  For example, to list the names of the Ennead gods, type "p" then select print from the drop-down list, then type a space followed by "E", then select EgyptianGod from the drop-down list and press Enter.

To perform a query, you specify a derivation rule to compute the facts requested by the query.  For example, the following query may be used to list the names of Shu's descendants.  The rule's head uses an anonymous predicate to capture the result derived from the rule's body.  The head variable gn is implicitly universally quantified.   The variables g1 and g2 introduced in the body are implicitly existentially quantified.

_(gn) <- hasGodName(g1:"Shu"), isanAncestorOf(g1, g2), hasGodName(g2:gn).

In LogiQL, queries are executed by appending their code in single quotes to the query command.  To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter.  The relevant query result is now displayed as shown in Figure 8.

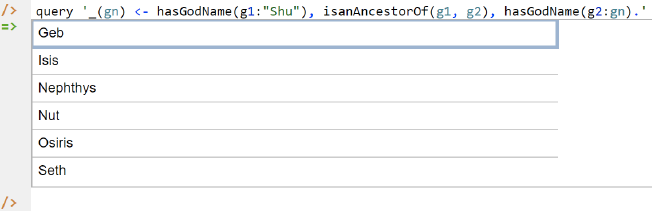
Figure 8.  A query to list the names of those Ennead gods descended from Shu.

Conclusion

The current article discussed how to declare recursive derivation rules and how to constrain relationships to be acyclic symmetric and/or strongly intransitive in ORM and LogiQL.  The next article will develop the Ennead example further, adding a frequency constraint.  The core reference manual for LogiQL is accessible at https://developer.logicblox.com/content/docs4/core-reference/.  An introductory tutorial for LogiQL and the REPL tool is available at https://developer.logicblox.com/content/docs4/tutorial/repl/section/split.html.  Further coverage of LogiQL may be found in [8].

References

[1]  S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995).  

[2]  M. Aref, B. Cate, T. Green, B. Kimefeld, D. Olteanu, E. Pasalic, T. Veldhuizen, & G. Washburn, "Design and Implementation of the LogicBlox System," Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York (2015).  http://dx.doi.org/10.1145/2723372.2742796  

[3]  R. Barker, CASE*Method:  Entity Relationship Modelling, Addison-Wesley:  Wokingham, England (1990).  

[4]  M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2," P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204.  

[5]  T.A. Halpin, Object-Role Modeling Fundamentals, Technics Publications:  New Jersey (2015).  

[6]  T.A. Halpin, Object-Role Modeling Workbook, Technics Publications:  New Jersey (2016).  

[7]  T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann:  San Francisco (2008).  

[8]  T.A. Halpin & S. Rugaber, LogiQL:  A Query language for Smart Databases, CRC Press:  Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939#  

[9]  T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.  

[10]  S. Huang, T. Green, & B. Loo, "Datalog and emerging applications:  an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011).  At:  http://dl.acm.org/citation.cfm?id=1989456  

[11]  Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013).  Available online at:  http://www.omg.org/spec/UML/2.5/Beta2/  

[12]  Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1, Object Management Group (2012).  Retrieved from http://www.omg.org/spec/OCL/2.3.1/  

Earlier Parts in this Series

[A]  T.A. Halpin, "Logical Data Modeling (Part 1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL:  http://www.BRCommunity.com/a2014/b760.html  

[B]  T.A. Halpin, "Logical Data Modeling (Part 2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL:  http://www.BRCommunity.com/a2014/b780.html  

[C]  T.A. Halpin, "Logical Data Modeling (Part 3)," Business Rules Journal, Vol. 16, No. 1 (Jan. 2015), URL:  http://www.BRCommunity.com/a2015/b795.html  

[D]  T.A. Halpin, "Logical Data Modeling (Part 4)," Business Rules Journal, Vol. 16, No. 7 (July 2015), URL:  http://www.BRCommunity.com/a2015/b820.html  

[E]  T.A. Halpin, "Logical Data Modeling (Part 5)," Business Rules Journal, Vol. 16, No. 10 (Oct. 2015), URL:  http://www.BRCommunity.com/a2015/b832.html  

[F]  T.A. Halpin, "Logical Data Modeling (Part 6)," Business Rules Journal, Vol. 17, No. 3 (Mar. 2016), URL:  http://www.BRCommunity.com/a2016/b852.html  

[G]  T.A. Halpin, "Logical Data Modeling (Part 7)," Business Rules Journal, Vol. 17, No. 7 (July 2016), URL:  http://www.BRCommunity.com/a2016/b866.html  

[H]  T.A. Halpin, "Logical Data Modeling (Part 8)," Business Rules Journal, Vol. 17, No. 11 (Nov. 2016), URL:  http://www.BRCommunity.com/a2016/b883.html  

[I]  T.A. Halpin, "Logical Data Modeling (Part 9)," Business Rules Journal, Vol. 18, No. 5 (May 2017), URL:  http://www.BRCommunity.com/a2017/b906.html  

[J]  T.A. Halpin, "Logical Data Modeling (Part 10)," Business Rules Journal, Vol. 18, No. 11 (Nov. 2017), URL:  http://www.BRCommunity.com/a2017/b929.html  

[K]  T.A. Halpin, "Logical Data Modeling (Part 11)," Business Rules Journal, Vol. 19, No. 4 (Apr. 2018), URL:  http://www.BRCommunity.com/a2018/b949.html  

# # #