This is the tenth article in a series on logic-based approaches to data modeling.  The first article^[A] briefly overviewed deductive databases and illustrated how simple data models with asserted and derived facts may be declared and queried in LogiQL,^{[2], [8], [10]} a leading-edge deductive database language based on extended datalog.^[1]  The second article^[B] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL.  The third article^[C] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.  The fourth article^[D] discussed how to declare external uniqueness constraints.  The fifth article^[E] covered derivation rules in a little more detail and showed how to declare inclusive-or constraints.  The sixth article^[F] discussed how to declare simple set-comparison constraints (i.e., subset, exclusion, and equality constraints) and exclusive-or constraints.  The seventh article^[G] explained how to declare subset, constraints between compound role sequences, including cases involving join paths.  The eighth article^[H] discussed how to declare exclusion and equality constraints between compound role sequences.  The ninth article^[I] explained how to declare basic subtyping in LogiQL.

The current article discusses how to declare relationships to be irreflexive (using a ring constraint) and symmetric (using a ring constraint or a derivation rule) in LogiQL.  The LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.

Irreflexive and Symmetric Ring Constraints

Table 1 shows an extract from a report that lists each country and which (if any) countries border it.  Each country is identified by its name and has zero or more countries that border it.  This example is based on an exercise from [7].  As an optional exercise, you might like to specify a data model for this example, including all relevant constraints, before reading on.

    Table 1.  Extract from a report listing each country and its bordering countries (if any).

Figure 1 shows one way to model this example with an Object-Role Modeling (ORM)^[5],[6],[7] diagram, using constructs discussed in previous articles.  Country is modeled as an entity type.  The appended exclamation mark indicates that Country is an independent object type, so may have instances (e.g., Australia) that exist independently of participating in any fact type other than its reference scheme.  This independence setting may be ignored in LogiQL, since it is assumed by default in the absence of a mandatory role constraint.  The preferred reference scheme for Country is depicted by the reference mode ".Name" shown in parenthesis.  The border information is modeled using the binary fact type Country borders Country.  The uniqueness constraint bar spanning this fact type indicates that this relationship is many-to-many.  The lack of any mandatory role dot on this fact type indicates that each of its roles is optional.

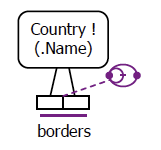
    Figure 1.  One way to model Table 1 in ORM notation, using two ring constraints.

The fact type Country borders Country is said to be a ring fact type since you can visualize a fact instance of it as navigating from an object in the Country type via the borders predicate back to an object in the same Country type, thus forming a ring.  Logical constraints that restrict how objects may relate via a ring predicate are called ring constraints.  Ring constraints are depicted in ORM by attaching the relevant ring constraint shape to the pair of constrained roles.  If the roles are contiguous, the constraint is attached to the junction of the two role boxes.

In Figure 1, the ring constraint shape is compound, combining two ring constraints.  The first ring constraint ensures that no country borders itself, as illustrated by the data in Table 1.  For example, Belgium cannot border Belgium.  In this case, the borders relationship is said to be irreflexive.

Notice that in Table 1 each pair of bordering countries is included twice in the data, once for each way of ordering the pair.  The second ring constraint ensures that if the fact that a given country borders another given country is recorded, then so is the inverse fact that the second country borders the first country.  For example, if Belgium borders France, then France must border Belgium.  In this case, the borders relationship is said to be symmetric.  Hence, in this example, the borders fact type is both irreflexive and symmetric.

In Figure 1, the ring constraint shape combines an irreflexive ring constraint shape with a symmetric ring constraint shape.  The figure below shows the intuition behind the constraint shapes.  The black shape at the top of Figure 2(a) suggests irreflexivity by using a dot for an object, a directed arrow for the relationship, and a stroke to indicate that the object cannot relate to itself via this relationship.  The violet shape below this is the actual shape used in ORM to depict irreflexivity.  The removal of the arrow-tip enables use of a smaller shape that can still be easily distinguished from other shapes.  The top shape in Figure 2(b) suggests a symmetric relationship that applies in both directions between two objects.  The actual, simplified constraint shape below it removes the arrow-tips.  Figure 2(c) shows how the combined constraint shape is composed by overlaying the two individual constraint shapes.

    Figure 2.  Combining an irreflexive ring constraint with a symmetric ring constraint.

For the example shown, the NORMA tool^[4] automatically verbalizes the irreflexive constraint as:  No Country borders itself.  The asymmetric constraint verbalizes thus:  If Country1 borders Country2 then it is impossible that Country2 borders Country1.

Figure 3(a) schematizes the same universe of discourse depicted in Table 1 as an Entity Relationship diagram in Barker notation (Barker ER).^[3]  The Barker ER schema depicts the primary reference scheme for Country by prepending an octothorpe "#" to the patient name attribute.  The asterisk "*" prepended to the country name attribute indicates that this attribute is mandatory.  The dashed line for the borders relationship indicates that each of its roles is optional for Country.  The crowsfoot at both ends indicate that the relationship is many-to-many.  Predicate readings are provided at each end of the relationship.  Barker ER has no graphic notation for ring constraints, so these constraints are not captured in the diagram.

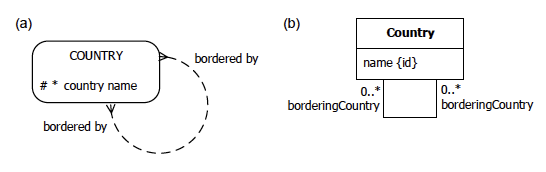
    Figure 3.  Basic data schema for Table 1 in (a) Barker ER, and (b) UML notation.

Figure 3(b) schematizes Table 1 as a class diagram in the Unified Modeling Language (UML).^[11]  The UML class diagram depicts the primary identification for Country by appending "{id}" to the name attribute.   The name and attribute by default has a multiplicity of 1, so is mandatory and single-valued.  The "0..*" multiplicities at the end of the borders association indicate that each country has zero or more bordering countries.  Names are provided for each association role.  UML has no graphic notation for ring constraints, so these constraints are not captured in the diagram.

The ORM schema in Figure 2 may be coded in LogiQL as shown below.   The right arrow symbol "->" stands for the material implication operator "→' of logic, and is read as "implies".   An exclamation mark "!" denotes the logical negation operator and is read as "it is not the case that".  A comma "," denotes the logical conjunction operator "&", and is read as "and".  Recall that LogiQL is case-sensitive; each formula must end with a period, and head variables are implicitly universally quantified.

The first line of the LogiQL code declares Country as an entity type whose instances are referenced by names that are coded as character strings.  The colon ":" in hasCountryName(c:cn) distinguishes hasCountryName as a refmode predicate, so this predicate is injective (mandatory, 1:1).  Comments are prepended by "//", and describe the constraint declared in the code immediately following the comment.  For example, the irreflexive ring constraint expressed in LogiQL as "!borders(c, c)" corresponds to the logical formula "∀c(Country c  →  ~ c borders c)".Country(c), hasCountryName(c:cn) -> string(cn).

borders(c1, c2) -> Country(c1), Country(c2).
// No country borders itself
!borders(c, c).
// If country c1 borders country c2, then c2 borders c1.
borders(c1, c2) -> borders(c2, c1).

To enter the schema in the free, cloud-based REPL tool, use a supported browser such as Chrome, Firefox, or Internet Explorer to access the website https://repl.logicblox.com.  Alternatively, you can access https://developer.logicblox.com/playground/, then click the "Open in new window" link to show a full screen for entering the code.

Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block.  After the "/>" prompt, type the letter "a", and click the addblock option that then appears.  This causes the addblock command (followed by a space) to be added to the code window.  Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code (see Figure 4).

    Figure 4.  Invoking the addblock command in the REPL tool.

Now copy the schema code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 5).  By default, the REPL tool also appends an automatically-generated identifier for the code block.   Alternatively, you can enter each line of code directly, using a separate addblock command for each line.

    Figure 5.  Adding a block of schema code.

The data in Table 1 may be entered in LogiQL using the following delta rules.  A delta rule of the form +fact inserts that fact.  Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes.  Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.

+Country(c1), +hasCountryName(c1:"Australia").
+Country(c2), +hasCountryName(c2:"Belgium"), +Country(c3), +hasCountryName(c3:"France"),
  +Country(c4), +hasCountryName(c4:"Germany"), +Country(c5), +hasCountryName(c5:"Luxembourg"),
  +Country(c6), +hasCountryName(c6:"Netherlands"), +Country(c7), +hasCountryName(c7:"Italy"),
  +Country(c8), +hasCountryName(c8:"Spain"), +Country(c9), +hasCountryName(c9:"Switzerland"),
  +borders(c2, c3), +borders(c2, c4), +borders(c2, c5), +borders(c2, c6),
  +borders(c3, c2), +borders(c3, c4), +borders(c3, c7), +borders(c3, c5), +borders(c3, c8), +borders(c3, c9),
  +borders(c4, c2), +borders(c4, c3),
  +borders(c5, c2), +borders(c5, c3),
  +borders(c6, c2),
  +borders(c7, c3),
  +borders(c8, c3),
  +borders(c9, c3).

Delta rules to add or modify data are entered using the exec (for 'execute') command.  To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list.  A space character is automatically appended.  Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules.  Now copy the lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  A new prompt awaits your next command (see Figure 6).

    Figure 6.  Adding the data.

Now that the data model (schema plus data) is stored, you can use the print command to inspect the contents of any predicate.  For example, to list the names of all the recorded countries, type "p" then select print from the drop-down list, then type a space followed by "C", then select Country from the drop-down list, and press Enter.  Alternatively, type "print Country" yourself and press Enter.  Figure 7 shows the result.  By default, the REPL tool prepends a column listing automatically-generated internal identifiers for the returned entities.   Similarly, you can use the print command to print the extension of the other predicates.

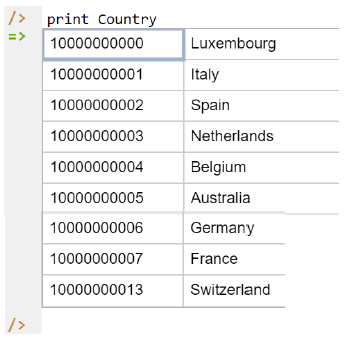
    Figure 7.  Using the print command to list the extension of Country.

As discussed in previous articles, to perform a query you specify a derivation rule to compute the facts requested by the query.  For example, the following query may be used to list the names of those countries that border Belgium.  The rule's head uses an anonymous predicate to capture the result derived from the rule's body.  The head variable cn is implicitly universally quantified.  The variables c1 and c2 introduced in the rule body are implicitly existentially quantified.

_(cn) <- hasCountryName(c1:cn), hasCountryName(c2:"Belgium"), borders(c1, c2).

In LogiQL, queries are executed by appending their code in single quotes to the query command.  To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter.  The relevant query result is now displayed as shown in Figure 8.

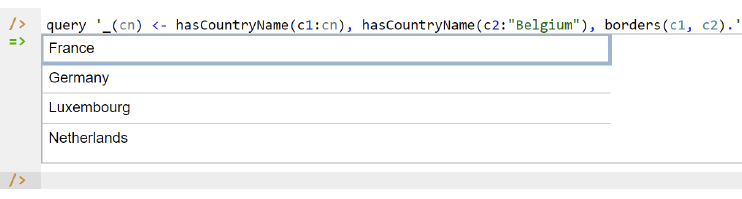
    Figure 8.  A query to list the names of those recorded countries that border Belgium.

Using a Derivation Rule to Ensure that a Relationship is Symmetric

With a symmetric relationship, you can enforce the symmetry either by a symmetric ring constraint, as discussed in the previous section, or by using a derivation rule.  We now consider the second approach. For ease of reference, the earlier countries report is repeated in Table 2, with the fact that Belgium borders France shown in blue and the fact that France borders Belgium shown in green.  Our LogiQL program will use the asserted predicate preborders(c1, c2) to mean that country c1 borders country c2, and the name of c1 alphabetically precedes the name of c2.  This alphabetic precedence is enforced by a constraint in the program, and green facts (where the first country name succeeds the second) are derived rather than being asserted, thus significantly reducing the data entry task.

    Table 2.  Extract from a report listing each country and its bordering countries (if any).

Figure 9 shows an ORM schema diagram for this approach, asserting the fact type Country preborders Country and deriving the fact type Country borders Country using the derivation rule shown.  The name precedence constraint for the preborders predicate is displayed as a footnoted, textual constraint with the footnote number appended to the relevant predicate reading.

    Figure 9.  The symmetric borders relationship is now derived.

The ORM schema in Figure 9 may be coded in LogiQL as follows.  The derivation rule uses "<-" for inverse implication (read as "if") and a semicolon ";" for inclusive logical disjunction (read as "or").

Country(c), hasCountryName(c:cn) -> string(cn).
// "preborders" means "borders, and its name alphabetically precedes"
preborders(c1, c2) -> Country(c1), Country(c2).
preborders(c1, c2), hasCountryName(c1:cn1), hasCountryName(c2:cn2) -> cn1 < cn2.
// No country preborders itself
!preborders(c, c).
// Country c1 borders c2 if either preborders the other
borders(c1, c2) <- preborders(c1, c2) ; preborders(c2, c1).

The sample data may be coded as shown below.  Note that the explicit assertions of border facts in inverse alphabetical order used in the previous section are omitted since these facts are now derivable.

+Country(c1), +hasCountryName(c1:"Australia").
+Country(c2), +hasCountryName(c2:"Belgium"), +Country(c3), +hasCountryName(c3:"France"),
  +Country(c4), +hasCountryName(c4:"Germany"), +Country(c5), +hasCountryName(c5:"Luxembourg"),
  +Country(c6), +hasCountryName(c6:"Netherlands"), +Country(c7), +hasCountryName(c7:"Italy"),
  +Country(c8), +hasCountryName(c8:"Spain"), +Country(c9), +hasCountryName(c9:"Switzerland"),
  +preborders(c2, c3), +preborders(c2, c4), +preborders(c2, c5), +preborders(c2, c6),
  +preborders(c3, c4), +preborders(c3, c7), +preborders(c3, c5), +preborders(c3, c8), +preborders(c3, c9).

The schema and data may be entered in the usual way.   As a sample query on this model, the following query returns the name of each country that borders both Belgium and Germany.  Notice that the result (France) preborders just one of these countries.

_(cn) <- hasCountryName(c1:cn), hasCountryName(c2:"Belgium"),
                  hasCountryName(c3:"Germany"), borders(c1, c2), borders(c1,c3).

Figure 10 shows a screenshot with the query result, based on the data provided.

    Figure 10.  A query to list the names of recorded countries that border both Belgium and Germany.

Conclusion

The current article discussed how to declare relationships to be irreflexive (using a ring constraint) and symmetric (using a ring constraint or a derivation rule) in LogiQL.  Future articles in this series will examine how LogiQL can be used to specify business constraints and rules of a more advanced nature, including further ring constraints and recursive derivation rules.  The core reference manual for LogiQL is accessible at https://developer.logicblox.com/content/docs4/core-reference/.  An introductory tutorial for LogiQL and the REPL tool is available at https://developer.logicblox.com/content/docs4/tutorial/repl/section/split.html.  Further coverage of LogiQL may be found in [8].

References

[1]  S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995).  

[2]  M. Aref, B. Cate, T. Green, B. Kimefeld, D. Olteanu, E. Pasalic, T. Veldhuizen, & G. Washburn, "Design and Implementation of the LogicBlox System," Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York (2015).  http://dx.doi.org/10.1145/2723372.2742796  

[3]  R. Barker, CASE*Method:  Entity Relationship Modelling, Addison-Wesley:  Wokingham, England (1990).  

[4]  M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2," P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204.  

[5]  T.A. Halpin, Object-Role Modeling Fundamentals, Technics Publications:  New Jersey (2015).  

[6]  T.A. Halpin, Object-Role Modeling Workbook, Technics Publications:  New Jersey (2016).  

[7]  T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann:  San Francisco (2008).  

[8]  T.A. Halpin & S. Rugaber, LogiQL:  A Query language for Smart Databases, CRC Press:  Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939#  

[9]  T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.  

[10]  S. Huang, T. Green, & B. Loo, "Datalog and emerging applications:  an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011).  At:  http://dl.acm.org/citation.cfm?id=1989456  

[11]  Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013).  Available online at:  http://www.omg.org/spec/UML/2.5/Beta2/  

[12]  Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1, Object Management Group (2012).  Retrieved from http://www.omg.org/spec/OCL/2.3.1/  

Earlier Parts in this Series

[A]  T.A. Halpin, "Logical Data Modeling (Part 1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL:  http://www.BRCommunity.com/a2014/b760.html  

[B]  T.A. Halpin, "Logical Data Modeling (Part 2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL:  http://www.BRCommunity.com/a2014/b780.html  

[C]  T.A. Halpin, "Logical Data Modeling (Part 3)," Business Rules Journal, Vol. 16, No. 1 (Jan. 2015), URL:  http://www.BRCommunity.com/a2015/b795.html  

[D]  T.A. Halpin, "Logical Data Modeling (Part 4)," Business Rules Journal, Vol. 16, No. 7 (July 2015), URL:  http://www.BRCommunity.com/a2015/b820.html  

[E]  T.A. Halpin, "Logical Data Modeling (Part 5)," Business Rules Journal, Vol. 16, No. 10 (Oct. 2015), URL:  http://www.BRCommunity.com/a2015/b832.html  

[F]  T.A. Halpin, "Logical Data Modeling (Part 6)," Business Rules Journal, Vol. 17, No. 3 (Mar. 2016), URL:  http://www.BRCommunity.com/a2016/b852.html  

[G]  T.A. Halpin, "Logical Data Modeling (Part 7)," Business Rules Journal, Vol. 17, No. 7 (July 2016), URL:  http://www.BRCommunity.com/a2016/b866.html  

[H]  T.A. Halpin, "Logical Data Modeling (Part 8)," Business Rules Journal, Vol. 17, No. 11 (Nov. 2016), URL:  http://www.BRCommunity.com/a2016/b883.html  

[I]  T.A. Halpin, "Logical Data Modeling (Part 9)," Business Rules Journal, Vol. 18, No. 5 (May 2017), URL:  http://www.BRCommunity.com/a2017/b906.html  

# # #