Verbalizing Business Rules (Part 15)
Business rules should be validated by business domain experts, and hence specified in a language easily understood by business people. This is the fifteenth in a series of articles on expressing business rules formally in a high-level, textual language. This article considers the verbalization of basic derivation rules.
The first article[1] discussed criteria for a business rules language, and verbalization of simple uniqueness and mandatory constraints on binary associations. Article two[2] examined hyphen-binding, and verbalization of internal uniqueness constraints that span a whole association, or that apply to n-ary associations. Article three[3] covered verbalization of basic external uniqueness constraints. Article four[4] considered relational-style verbalization of external uniqueness constraints involving nesting or long join paths, as well as attribute-style verbalization of uniqueness constraints and simple mandatory constraints. Article five[5] discussed verbalization of mandatory constraints on roles of n-ary associations, and disjunctive mandatory constraints (also known as inclusive-or constraints) over sets of roles.
Article six[6] considered verbalization of value constraints. Article seven[7] examined verbalization of subset constraints. Article eight[8] discussed verbalization of equality constraints. Article nine[9] covered verbalization of exclusion constraints. Article ten[10] dealt with verbalization of internal frequency constraints on single roles. Article eleven[11] considered verbalization of multi-role, and external, frequency constraints. Article twelve[12] discussed verbalization of ring constraints. Article thirteen[13] covered verbalization of basic subtype constraints. Article fourteen[14] discussed the need for subtype definitions, and how to verbalize them.
Derived Fact Types
Many business domains include information
that is derived from other information. As a simple example, suppose
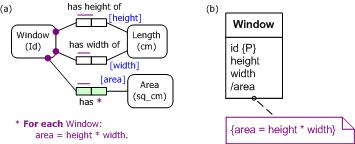
we are interested in knowing the height, width, and area of various windows.
If we know the height and width of a window, we can compute its area simply by multiplying
its height by its width. Figure 1 models this situation in ORM 2[16] and UML[17]
notations. From an ORM perspective, we have three fact types: Window has height of Length; Window
has width of Length; and Window
has area. The asterisk "*" postfix on the area fact
type indicates that it is derived, and the textual derivation rule declares
how it is derived from the other fact types. In UML, the three fact types are
all depicted as attributes. A slash "/" prefix indicates the derived
attribute, and an attached note provides the derivation rule. The {P} notation
in the UML figure is a non-standard extension indicating preferred identification
scheme (and hence mandatory and unique). As industrial versions of Entity-Relationship
(ER) modeling typically provide no graphical means of depicting derived information,
we ignore them in this article.
Figure 1. Derived fact type for area in (a) ORM 2 and (b) UML notation.
In this example, both ORM and UML express the derivation rule in attribute style, where area, height, and width may be viewed as attributes of Window. To enable this, the ORM schema includes the relevant role names (shown in square brackets) to be used as attribute names in rule verbalization. ORM uses a for-each clause to declare the context of the rule. Within the rule, "*" denotes multiplication.
In ORM 2, a derivation rule may be specified in attribute style, relational style, or mixed style. Relational style verbalizes relationships directly using predicate readings. For example, the derivation rule for area may be specified in relational style thus:
Define Window has Area(sq_cm) asWindow has height of Length1 andWindow has width of Length2 andArea = Length1 * Length2.
In cases like this where the derivation rule involves simple arithmetic, attribute style is typically more compact and readable than relational style. Mixed style allows fact types to be specified using predicate readings and role names within the same rule.
Partly Derived Fact Types
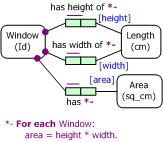
A fact type that is not derived using other fact types is said to be primitive. Here the height and width fact types are primitive, and the area fact type is derived. Notice that the equation area = height * width has three variables, with one degree of freedom. In principle, any of these three variables could have been chosen as derived, with the others primitive. For example, if we know the area and height, we can derive the width. And if we know the area and width, we can derive the height. At a more fundamental level then, the rule verbalization
For each Window:area = height * width.
may be considered a constraint that restricts the possible triples of values that may be assigned to area, height, and width. Although "area" is mentioned first in the equation above, there is nothing in the underlying logic that forces us to say that this is the only quantity that can be derived. In principle, one could allow any two values in the triple to be entered (area and height, or area and width, or height and width), then use this constraint to determine the other value. To indicate this intent in ORM 2, each of the fact types is marked "*-" signifying partly derived, and the derivation rule is flagged this way too.
Figure 2. The fact types are partly derived: an instance of any one may be derived from the others.
Using "iff"
to abbreviate "if and only if", the relational version of the rule may
also be specified as a mere constraint thus:
Window has Area(sq_cm) iffWindow has height of Length1 andWindow has width of Length2 andArea = Length1 * Length2.
While it would be unusual to apply partial derivation in this Window example, this technique is of practical use in applications such as loan selections, where one might want to enter, say, any two of percentage rate, loan amount, and desired loan term, to see what the other figure will be.
Once we decide that we will use the constraint simply to derive
the area, this choice is reflected by marking the area fact type as fully derived
in the schema diagram (with an asterisk in ORM, and a slash in UML). The left
hand side of the attribute style equation, or the head of the relational style "iff" rule, is now understood
to be the derived quantity, and the "Define
as" relational version of the rule may also be used.
Dot Notation and Of-Notation
When the derivation rule is based on conceptual joins rather than mathematical
operations, the relational style of rule verbalization is often more natural.
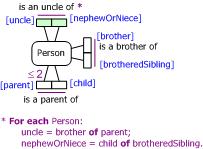
For example, see the ORM rule for deriving the fact type Person
is an uncle of Person in Figure 3(a). Here subscripts
are used to distinguish different occurrences of the Person variable. For simplicity,
the relevant ring constraints[12] are omitted. In ORM, each fact
type must have at least one relationship reading, whereas role names are optional.
A UML class diagram for this situation is shown in Figure 3(b). In UML, associations must have role names, whereas a relationship reading is optional. When roles of an association are played by instances of the same class, distinct role names must be provided to disambiguate expressions that use role names for navigating the schema, as in this example. Here both the uncle role and the nephewOrNiece role are derived. Their derivation rules make use of the dot notation familiar to programmers.
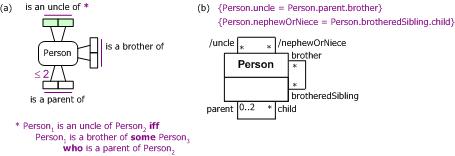
Figure 3. Derivation of Unclehood in (a) ORM and (b) UML.
As an alternative to the dot notation, ORM 2 allows the of-notation.
This works in a similar way to the dot notation, except the order is reversed.
For example, instead of "parent.brother"
we have "brother of parent"
(see Figure 4). Use of this notation requires that the relevant role names
are supplied. In most cases, the of-notation is likely to be more readable
than the dot notation to non-technical business people.
Figure 4 Use of role names and the of-notation.
Summary Derivations
Many derivations are of a summary nature, where the information held in the derived fact type instance captures only part of the information in the fact type instances (primitive or derived) used to derive it. In such cases, there is only one choice as to which of many fact types may be selected for derivation (unlike the area equation discussed earlier). For example, you can derive a grade point average from a set of grades, but you can't derive the set of grades from the average. Likewise, you can derive your age in years from your birth date and the current date, but not vice versa.
As a classic business example, consider the line item schema shown in Figure 5. A line item is identified by combining its line number and its order (shown in ORM 2 by the circled double line, and in UML by an informal note). We compute line totals as the product of the quantity and unit price. Although unlikely, in principle we could have chosen instead to compute the quantity from the unit price and line total. However, the total charge for the order however must be derived, since it is computed by summing the individual line totals for that order. We cannot derive the line totals from the total charge, since there are many possible sets of line totals that would result in the same total charge for the order.
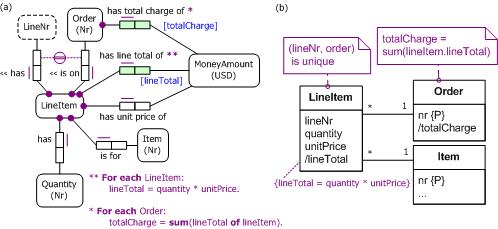
Figure 5. Deriving line totals and order totals in (a) ORM and (b) UML.
Lazy and Eager Evaluation
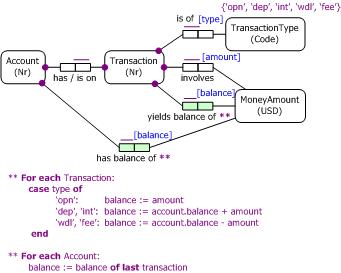
Typically, instances of derived fact types are derived on query (the computation to derive them is not performed until requested). This is known as lazy evaluation (don't evaluate until you have to). In such cases, the derived facts need not be stored. In rare cases, however, the business may decide to derive on update, performing the calculation as soon as the underlying facts used in the derivation are updated. This is called eager evaluation. In such cases, the derived facts are actually stored. This is indicated in ORM by marking the fact type to be derived and stored with a double asterisk "**".
As a practical example, the ORM schema in Figure 6 declares that account balances are to be derived on update and then stored. This simplifies the derivation rule to compute balances, and enables better performance, since only the current transaction and the immediately previous transaction (if any) need to be accessed to compute the current balance. An historical record is maintained for transaction balances, while a single value is stored for the current account balance.
Figure 6. Account balances are derived on update, and then stored.
A simplified specification of the derivation rules is shown. This assumes
that the only types of transaction types are opn
(open account with an initial, possibly zero deposit), dep
(later deposit), int (interest
earned), wdl (withdrawal), and
fee (bank fee). Also, predefined
semantics for last are
assumed (based on the highest transaction number for the account). Though not
shown here, this example also illustrates one of those rare cases requiring an immutable
constraint (called "frozen" in UML) to make the transactions immutable,
in this case for auditing purposes.
While the syntax of the rules resembles that of a programming language, it is
arguably still high level enough to be understood by a non-technical domain expert.
Alternative syntaxes are possible to make the rules more readable. For example,
"is assigned the value of"
may be used instead of ":=", and the case-clause may be replaced by a set
of if-clauses. The syntax of ORM's textual language for derivation rules and
constraints is still being refined, so this is meant to be illustrative only.
It is quite a challenge to design a formal language that is rich enough to capture
complex rules, while still being intelligible to non-technical people.
References
[1] T.A. Halpin. "Verbalizing Business Rules
(Part 1)," Business Rules Journal, Vol. 4, No. 4 (April 2003).
URL: http://www.BRCommunity.com/a2003/b138.html ![]()
[2] T.A. Halpin. "Verbalizing Business Rules
(Part 2)," Business Rules Journal, Vol. 4, No. 6 (June 2003). URL: http://www.BRCommunity.com/a2003/b152.html ![]()
[3] T.A. Halpin. "Verbalizing Business Rules
(Part 3)," Business Rules Journal, Vol. 4, No. 8 (August 2003).
URL: http://www.BRCommunity.com/a2003/b163.html ![]()
[4] T.A. Halpin. "Verbalizing Business Rules
(Part 4)," Business Rules Journal, Vol. 4, No. 10 (October 2003).
URL: http://www.BRCommunity.com/a2003/b172.html ![]()
[5] T.A. Halpin. "Verbalizing Business Rules
(Part 5)," Business Rules Journal, Vol. 5, No. 2 (February 2004).
URL: http://www.BRCommunity.com/a2004/b179.html ![]()
[6] T.A. Halpin. "Verbalizing Business Rules
(Part 6)," Business Rules Journal, Vol. 5, No. 4 (April 2004).
URL: http://www.BRCommunity.com/a2004/b183.html ![]()
[7] T.A. Halpin. "Verbalizing Business Rules
(Part 7)," Business Rules Journal, Vol. 5, No. 7 (July 2004). URL: http://www.BRCommunity.com/a2004/b198.html ![]()
[8] T.A. Halpin. "Verbalizing Business Rules
(Part 8)," Business Rules Journal, Vol. 5, No. 9 (September 2004).
URL: http://www.BRCommunity.com/a2004/b205.html ![]()
[9] T.A. Halpin. "Verbalizing Business Rules
(Part 9)," Business Rules Journal, Vol. 5, No. 12 (December 2004).
URL: http://www.BRCommunity.com/a2004/b215.html ![]()
[10] T.A. Halpin. "Verbalizing Business Rules
(Part 10)," Business Rules Journal, Vol. 6, No. 4 (April 2005).
URL: http://www.BRCommunity.com/a2005/b229.html ![]()
[11] T.A. Halpin. "Verbalizing Business Rules
(Part 11)," Business Rules Journal, Vol. 6, No. 6 (June 2005).
URL: http://www.BRCommunity.com/a2005/b238.html ![]()
[12] T.A. Halpin. "Verbalizing Business Rules
(Part 12)," Business Rules Journal, Vol. 6, No. 10 (October 2005).
URL: http://www.BRCommunity.com/a2005/b252.html ![]()
[13] T.A. Halpin. "Verbalizing Business Rules
(Part 13)," Business Rules Journal, Vol. 6, No. 12 (December 2005).
URL: http://www.BRCommunity.com/a2005/b261.html ![]()
[14] T.A. Halpin, "Verbalizing Business Rules (Part
14)," Business Rules Journal, Vol. 7, No. 4 (April 2006), URL: http://www.BRCommunity.com/a2006/b283.html ![]()
[15] T.A. Halpin. Information Modeling and Relational Databases. Morgan Kaufmann: San Francisco, 2001.
[16] T.A. Halpin, "ORM 2," On the Move to
Meaningful Internet Systems 2005: OTM 2005 Workshops, eds. R. Meersman, Z. Tari,
P. Herrero, et al. Cyprus: Springer LNCS 3762, pp. 676-87, 2005. ![]()
[17] Object Management Group. UML 2.0 Infrastructure.
Object Management Group, 2003. URL: http://www.omg.org/uml ![]()
[18] Object Management Group. UML 2.0 Object Constraint Language. Object Management Group, 2003. URL: http://www.omg.org/uml
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules