Ontological Modeling (Part 2)
This is the second in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL). OWL is based on description logic. A later series of articles will explore other logic-based languages such as Datalog. The previous article[2] provided a simple introduction to ontologies and the Semantic Web and covered most of the basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. This second article discusses the N3 notation for RDF and covers the basics of RDF Schema.
Notation 3 for RDF (N3)
As discussed in the previous article, RDF statements are essentially binary relationship instances represented as (subject, predicate, object) triples. Subjects and predicates are treated as resources, so are identified by Uniform Resource Identifier references (URIrefs), which provide document-independent, global identifiers, composed of a Uniform Resource Indicator (URI), optionally followed by "#" and a local fragment identifier (e.g., http://www.w3.org/TR/rdf-primer/#basicconcepts). Objects are either resources or literals (constants). Literals may be untyped (e.g., "Australia") or typed (e.g., 63: xsd;nonNegativeInteger).
While facilitating exchange, the lengthy identifiers provided by URIrefs lead to long-winded statement formulations. For example, the following statement, spread over three lines, might be used to declare CS600 as a course in a program offered at Galactic University.
http://www.galacticUni.edu/programs#CS600
http://www.w3.org/1999/02/22-rdf-syntax-ns#type
http://www.galacticUni.edu/programs#Course
Notice that the URI typically consumes most of the identifier. In this example, each URI is a Uniform Resource Location (URL). Imagine storing thousands of statements about academic programs at Galactic University in a single document housed at http://www.galacticUni.edu/programs. Almost all of these statements would use the same URL (http://www.galacticUni.edu/programs), which effectively provides a namespace in which names such as 'CS600' are locally identifying. It would be painful to keep on entering the same URL for all those statements. Mainly to save writing and improve readability, Tim Berners-Lee introduced a simplified notation for RDF called Notation 3 (N3). Among other tasks, Tim is the editor of a World Wide Web Consortium (W3C) committee that oversees the specification of the notation.[3]
In N3, you can predeclare namespace prefixes to denote URI namespaces and then use those prefixes later as shorthand for full URIs when identifying resources. The prefixes are declared using an @prefix command to introduce a prefix name and the URI it abbreviates, with the URI (including #) delimited in angle brackets, i.e.,
@prefix namespacePrefix <URI#>.
Identifiers using such namespace prefixes are called qualified names (qnames) and are formed by prepending the prefix to a colon ":" followed by the local identifier. The BNF syntax is
qname ::= namespacePrefix : name
When qnames are used, statement triples are terminated by a period ".". For example, suppose we declare the prefixes rdf and gup as follows.
@prefix rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#>
@prefix gup: <http://www.galacticUni.edu/programs#>
The previous fact about CS600 may now be formulated more briefly as follows.
gup:CS600 rdf:type gup:Course.
Using the previous prefix declarations, this N3 statement is interpreted as equivalent to the longer RDF statement mentioned earlier. N3 treats "a" as a reserved word that is shorthand for "rdf:type", so the above statement may be shortened even further to
gup:CS600 a gup:Course.
In English, you can read this as "In the context of the gup namespace, CS600 is a Course", where "is a" means "is an instance of". Here the terms CS600, a, and Course are effectively being used within the declared namespace to denote a resource. They are like individual constants within the scope of the declared namespace. Informally, you probably thought of 'CS600' as a course code, but the RDF statement doesn't actually tell us this. If you want to state this explicitly, you could add a statement such as
gup:CS600 gup:hasCourseCode "CS600".
There is no requirement in RDF to identify the type of a resource. So we could make a statement such as the following without knowing that CS600 is a course.
gup:CS600 gup:hasCreditPointValue "10".
Notice that this way of making statements about things that could be untyped is very different from the way things are done in information modeling approaches such as Object-Role Modeling (ORM), the Unified Modeling Language (UML), and Entity Relationship modeling (ER).[1] In each of those approaches, we would declare a Course type (e.g., a Course entity type or a Course class) and treat 'CS600' as a course code of an instance of that type.
In N3, the prefix in a qname may be empty, so the qname starts with a colon (e.g., :CS600). By default, the empty prefix "" treats the namespace to be the local document. For example, if we are currently at the location http://www.galacticUni.edu/programs, then the following three statements
gup:CS600 a gup:Course.
gup:CS600 gup:hasTitle "Advanced Informatics".
gup:CS600 gup:hasCreditPointValue "10".
may be written more briefly as
:CS600 a :Course.
:CS600 :hasTitle "Advanced Informatics".
:CS600 :hasCreditPointValue "10".
As a further abbreviation, N3 allows use of a semicolon to assume the same subject. So the above three statements about the subject CS600 may be declared more briefly thus
:CS600 a :Course;
:hasTitle "Advanced Informatics";
:hasCreditPointValue "10".
In general, a statement list of the form
subject1 predicate1 object1.
subject1 predicate2 object2.
…
subject1 predicaten objectn.
may be abbreviated to
subject1 predicate1 object1;
predicate2 object2; …
predicaten objectn.
As another abbreviation, N3 allows use of a comma to assume the same subject and predicate. In other words, you can use a comma as a separator in an object list. Consider, for example, the following two statements (presumably made in a biblical namespace)
:Adam :isFatherOf :Cain.
:Adam :isFatherOf :Abel.
Here we have the same subject and predicate applied to two objects. Using a comma to separate the objects, these two statements may be abbreviated thus
:Adam :isFatherOf :Cain, :Abel.
Before introducing the next aspect of N3, let's review some basic logic. Suppose we are given the following dictionary, where a is an individual constant, P is a unary predicate, and B is a binary predicate.
a = Australia
Px = x is a person
xBy = x was born in y
The proposition 'Somebody was born in Australia' may be expressed in predicate logic as follows, using ∃ for the existential quantifier (there exists) and & for conjunction (logical and).
∃x(Px & xBa)
Using the dictionary supplied, you can read this as: there exists something (let's call it x), such that x is a person and x was born in Australia.
N3 has various ways to support existential quantifiers. The most common way is to use square brackets to enclose triples that have the same "blank node" as their subject. The term "blank node" may be shortened to "bnode". A blank node in RDF is like an anonymous variable in Prolog or Datalog and may be read as 'something'. However, in N3 you can have multiple anonymous variables (e.g., _:x, _:y) using the same variable within a formula to indicate binding to the same existential quantifier. This can also be accomplished by the square bracket notation, since all predicate-object pairs within the same square brackets are understood to be bound to the same, implicit, existential quantifier. For example, assuming the namespace is the current document, the proposition 'Somebody was born in Australia' (i.e., ∃x(x is a person & x was born in Australia)) may be expressed in N3 using a blank node thus
[ a :Person; :wasBornIn :Australia ].
In general, a blank node formula is equivalent to an existentially quantified formula as shown below. A blank node has scope only within its immediate expression. No nesting of blank node expressions is permitted.
[ predicate object ] ≡ ∃x(x predicate object)
If a blank node expression is used as the object of an outer predicate, then the existential quantifier is understood to prepend the outer subject. Using a for the initial subject, R and S for predicates, and b for the final object, the following equivalence applies.
a R [ S b ] ≡ ∃x(aRx & xSb)
i.e., a R [ S b ] may be read as a R's something that S's b.
For example, assuming the local namespace, the following expression may be used to translate the proposition 'Terry is a parent of somebody who was born in Australia'
:Terry :isParentOf [ a :Person; :wasBornIn :Australia].
As an example with two blank nodes, and assuming the local namespace, the following expression translates the proposition 'Somebody with family name 'Obama' is president of some country'
[ a :Person; :hasfamilyName "Obama"] :isPresidentOf [ a :Country].
In predicate logic this corresponds to
∃x(Person x & x hasFamilyName 'Obama' & ∃y(x isPresidentOf y & Country y))
Note that relational databases as well as popular information modeling approaches such as ORM, UML, and ER typically do not store existential statements like those just considered. Such statements can easily be derived from more specific data, but it would be highly unusual to store them in that form. This again reflects the freedom in RDF to basically say whatever you want.
In addition to providing a more compact and readable syntax for RDF, N3 includes quantifiers (e.g., @forAll and @forSome) to facilitate the formulation of rules, and it also allows braces "{", "}" to be used for quoting so that statements can be made about statements. Further details about these and other features may be found on the N3 Website.[3]
Basics of RDF Schema (RDFS)
RDF Schema (RDFS) builds on RDF by adding formal support for classes and subclassing, which we now discuss. In addition, RDFS supports specialization and subsetting of predicates (see next article). The full specification of RDFS is available on a W3C Website.[4] Resources may be typed as instances of classes using the predefined rdfs:Class. For example, Person and Book may be declared to be classes thus
:Person rdf:type rdfs:Class.
:Book rdf:type rdfs:Class.
Using N3's "a" to abbreviate "rdf:type", these type declarations may be rendered more briefly thus
:Person a rdfs:Class.
:Book a rdfs:Class.
In RDFS, use of the rdf:type (or N3 'a') predicate implies that the object is a class. For example, the following statement asserts not only that the resource :Elvis is an instance of the resource :Singer, but also that :Singer is a class.
:Elvis a :Singer.
RDFS predefines the rdfs:subClassOf predicate to indicate that the subject is a subclass of the object. A statement of the form A rdfs:subClassOf B also implies that both A and B are classes. The rdfs:subClassOf predicate is transitive, allowing simple inferences to be drawn. For example, given any resources A, B, and C, the following two statements
A rdfs:subClassOf B
B rdfs:subClassOf C
enable us to infer
A rdfs:subClassOf C.
For example, given
:MaleSinger a :Singer.
:Singer a :Person.
we may infer :MaleSinger a :Person.
Using "⊆" for "is a subclass of", "&" for "and", and "→" for "implies", this transitivity rule may be written thus:
(A ⊆ B & B ⊆ C) → A ⊆ C. We can picture this graphically as shown in Figure 1.
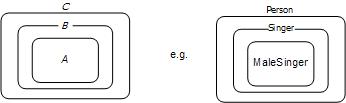
Figure 1. Subclassing is transitive: (A ⊆ B & B ⊆ C) → A ⊆ C.
Further inferences may be drawn by using the rdf:type and rdfs:subClassOf predicates in combination. Given any resources a, B, and C, where a is in instance of B, and B is a subclass of C, we may infer that a is an instance of C. For example, from
:Elvis a :Singer.
:Singer rdfs:subClassOf :Person.
we may infer
:Elvis a Person.
Using "∈" for "is an instance of" and "⊆" for "is a subclass of", this composite transitivity rule may be written thus: (a ∈ B & B ⊆ C) → a ∈ C. We can picture this graphically as shown in Figure 2.

Figure 2. Composite transitivity: (a ∈ B & B ⊆ C) → a ∈ C.
In mathematics, binary relations are often treated as sets of ordered pairs, indicating how elements in the domain (the set of elements on the left-hand side) map to elements in the range (the set of elements on the right-hand side of the relation). Figure 3(a) depicts an abstract example of a many-to-one (n:1) relation where one or more items in the domain map to a single item in the range. Binary relations may also be 1:n, m:n, or 1:1. Figure 3(b) depicts a concrete example, using the binary predicate has_square, where the domain is the set of numbers {-2, -1, 0, 1, 2} and the range is the set {0, 1, 4}.
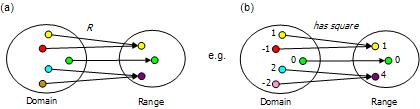
Figure 3. A binary relation maps domain items to range items.
RDFS effectively allows predicates to be 'typed', by restricting their domain and range to a specified class. The predefined predicate rdfs:domain (meaning "has domain") is used to restrict a predicate's subject to a given domain. The predefined predicate rdfs:range (meaning "has range") is used to restrict a predicate's object to a given domain. The syntax is thus
predicate rdfs:domain domain.
predicate rdfs:range range.
For example, consider Person drives Car as an ORM fact type, ER relationship, or UML association. In RDFS you can declare this roughly as follows:
:drives rdfs:domain :Person.
:drives rdfs:range :Car.
The object of an rdfs:domain predicate or rdfs:range predicate is implied to be a class, so the above two statements imply that :Person and :Car are classes.
RDFS allows the same predicate to be assigned multiple domains, in which case, instances of its subject are restricted to the intersection of those domains. Similarly, a predicate may be assigned multiple ranges, thus satisfying all of them. Hence each declared subject of a predicate is known to belong to the domain(s) of that predicate, and each declared object of a predicate is known to belong to the range(s) of that predicate. For example, from the following three statements
:sings rdfs:domain :Person.
:sings rdfs:range :Song.
:Elvis :sings :AllShookUp.
we may infer the following two statements
:Elvis a :Person.
:AllShookUp a :Song.
Conclusion
This article introduced the N3 notation for the Resource Description Framework (RDF) and then discussed basic features of RDF Schema (RDFS). The next article will complete the coverage of RDFS and provide an overview of different flavors of the Web Ontology language (OWL). Later articles will examine OWL in some depth.References
[1] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[2] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html ![]()
[3] W3C, Notation 3 (N3): A Readable RDF Syntax, ed. T. Berners-Lee, (2006). URL: http://www.w3.org/DesignIssues/Notation3 ![]()
[4] W3C, RDF Vocabulary Description Language 1.0: RDF Schema, (2004). URL: http://www.w3.org/TR/rdf-schema/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules