Ontological Modeling (Part 10)
This is the tenth in a series of articles on ontology-based approaches to modeling. The main focus is on popular ontology languages proposed for the Semantic Web, such as the Resource Description Framework (RDF), RDF Schema (RDFS), and the Web Ontology Language (OWL). OWL is based on description logic. A later series of articles will explore other logic-based languages such as datalog.
The first article[2] introduced ontologies and the Semantic Web, and covered basic concepts in the Resource Description Framework (RDF), contrasting them with other data modeling approaches. The second article[3] discussed the N3 notation for RDF, and covered the basics of RDF Schema. The third article[4] provided further coverage of RDFS, and introduced different flavors of the Web Ontology language (OWL). The fourth article[5] discussed basic features of OWL, mainly using Manchester syntax. The fifth article[6] discussed OWL taxonomy, comparison operators for classes, data types and predicates, and examined inverses, functional roles and keys in more depth. The sixth article[7] covered cardinality restrictions in OWL 2. The seventh article[8] discussed the union, intersection, and complement operators in OWL 2. The eighth article[9] explored support for ring constraints within OWL 2. The ninth article[10] discussed enumerated types as well as value restrictions on properties in OWL 2. The current article examines OWL 2's support for property chains and compares this with related concepts in data modeling approaches.
Property Chains in OWL 2
As discussed in earlier articles, in OWL an object property is a binary predicate used to state facts of the form subject predicate object, where both subject and object are entities (i.e., individuals that are identified by Internationalized Resource Identifiers). OWL 2 allows you to derive a new object property fact by composing two or more object property facts together in a chain, where the entity in the object position of one fact (other than the last fact) is also the subject of the following fact. In relational database work, this corresponds to performing an equijoin between two elementary relations and then projecting on the first and last attribute in the chain. In OWL, the equijoin operation is known as a composition operation, and an expression that composes two or more predicates is called a property chain.
To illustrate this notion, consider a business domain in which each person is born in exactly one city, and each city is located in exactly one country. Figure 1(a) depicts a basic schema for this in the notation of Object-Role Modeling (ORM).[1] Figure 1(b) models it as a Unified Modeling Language (UML) class diagram.[11] For simplicity, the reference schemes for persons, cities, and countries are omitted, but you may assume that this domain is small enough so that all entities may be identified by their names.
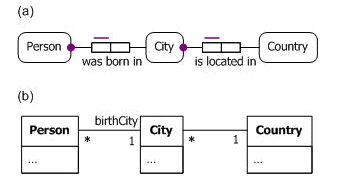
Figure 1. A simplified schema about births and city locations in (a) ORM and (b) UML.
Using OWL syntax discussed in earlier articles in this series, one way of specifying this schema in OWL using Manchester syntax is as follows:
ObjectProperty: wasBornInCity
Domain: Person
Range: CityObjectProperty: isLocatedInCountry
Domain: City
Range: CountryClass: Person
SubClassOf: wasBornInCity exactly 1Class: City
SubClassOf: isLocatedInCountry exactly 1
Now suppose we are also interested in knowing which countries people are born in. As shown in Figure 2(a) and Figure 2(b), this may be catered for in ORM by adding the derived fact type Person was born in Country, together with a derivation rule to infer the birth country facts. In ORM, derived fact types are marked with an asterisk, and derivation rules may be specified textually in FORML, using (a) relational-style or (b) attribute style. Relational-style rules use "iff" to abbreviate "if and only if" and predicate readings to navigate across predicates. Attribute style rules use role names (shown in square brackets) for navigation, and may use either of-notation (shown here) or dot-notation (e.g., Person.birthCountry = Person.birthCity.country). As shown in Figure 2(a), in UML derived attributes or derived associations are marked with a slash, and derivation rules may be specified in the Object Constraint Language (OCL),[12] which also uses a dot-notation.
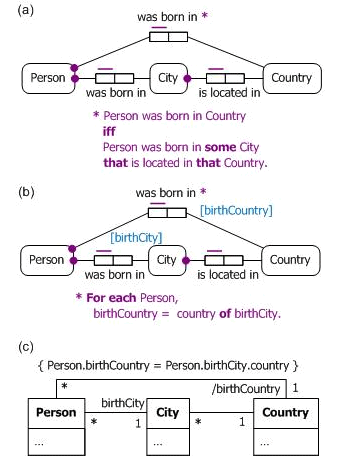
Figure 2. Deriving people's birth countries in (a) ORM, (b) ORM, and (c) UML.
In OWL 2, we can do something similar by declaring the wasBornInCountry predicate to be a subproperty of the predicate formed by projecting on the start and end of the property chain that composes the wasBornCountry and isLocatedInCity predicates. In Manchester Syntax, the property chain is specified using the symbol "o" as the composition operator placed between adjacent predicates in the chain, and listed after the header "SubPropertyChain: ". For example, Table 1 shows the relevant extension to the previous OWL statements needed to specify the relevant subproperty declaration in Manchester Syntax. As also shown in the table, in Turtle syntax the predicates being composed are listed in parentheses as the argument of the owl:propertyChainAxiom predicate.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: wasBornInCountry |
:wasBornInCountry
owl:propertyChainAxiom |
In description logic, this kind of subproperty declaration is called a complex role inclusion. In classical logic, the above declaration may be formulated as follows, using "→" for "implies" and using "&" for "and".
∀x,y,z [(x wasBornInCity y & y isLocatedInCountry z) → x wasBornInCountry z]
OWL adopts the same semantics for its statements as in first-order logic. So, the OWL property chain subproperty statement given earlier simply means the following: Given any individual objects x, y, and z, for each interpretation, or state of the world, in which it is true that x was born in city y and y is located in country z it is also true that x was born in country z. For example, if we know that Einstein was born in the city Ulm, and that Ulm is located in the country Germany, we may infer that Einstein was born in Germany.
In the ORM schema of Figure 2(a), the derivation rule uses "iff" indicating an equivalence, not just an implication. In addition, the birth country fact type is marked as being derived from the birth city and city location fact types, whose instances are treated as simply asserted. In such cases, you may think of the derivation rule as providing a definition for the derived fact type. The UML class diagram in Figure 2(b) may be interpreted in a similar way.
However, subproperty statements in OWL simply declare implications, not equivalences, so do not strictly provide definitions. To make this clearer, let us widen our sample business domain to include persons who are not born in cities (e.g., people born on a ship, or on an airplane, or in a small village that we don't treat as a city). Let us also assume that facts about which countries people are born in cannot be directly asserted, only derived. Figure 3 shows how this may be modeled in ORM and UML. In this case, the birth city and birth country roles are now optional for Person, and the ORM derivation rule is softened to an if-rule.
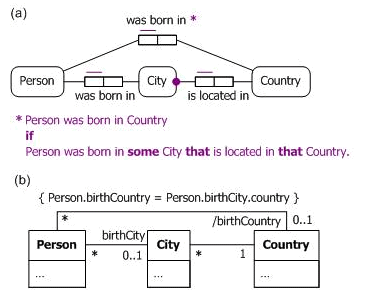
Figure 3. One way of modeling birth country derivation for just some people in (a) ORM and (b) UML.
In OWL, the optionality of the birth city predicate is indicated by softening the earlier restriction "SubClassOf: wasBornInCity exactly 1" to a functional declaration, thus:
ObjectProperty: wasBornInCity
Characteristics: Functional
However, the subproperty declaration given earlier remains unaltered. As before, the implication holds in one direction only.
Now let us modify the business domain just considered to allow some birth country facts to be simply asserted, while other birth country facts may be derived. For example, I can assert that I was born in Australia without telling you the city in which I was born. You can derive Einstein's birth country from the facts I gave you earlier, but you can't derive my birth country. This may be modeled in ORM as shown in Figure 4.
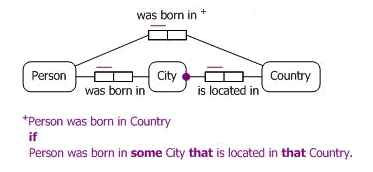
Figure 4. Modeling birth country facts using a semiderived fact type in ORM.
Here the fact type Person was born in City is semiderived, meaning that some of its instances may be simply asserted and some instances may be derived. Semiderived fact types and their associated derivation rules are marked with a plus superscript "+" (intuitively, half an asterisk). UML has no such feature.
In OWL, this situation would be modeled using the same declarations as in the previous example. The subproperty declaration is again just a simple implication that applies to any satisfying models. There is currently no way in OWL to distinguish between the two different approaches taken in Figure 3 and Figure 4. Hence, OWL is not concerned with choices about how to actually implement implications. Moreover, while OWL enables implication statements to be used to make inferences, it does not treat implication statements as integrity constraints. The next article discusses this point further, analyzing in depth the implementation differences between constraints and derivation rules, and contrasting OWL with other data modeling approaches in this regard.
Property Chains Involving Multiple Occurrences of the Same Predicate
A property chain may compose multiple occurrences of the same predicate. Figure 5 provides a simple example in both ORM and UML, where grandparenthood facts are derived by composing two parenthood facts. As shown, ORM derivation rules in relational style use subscripts to distinguish individual variables based on the same object type. In attribute style, the ORM derivation rule may be reformulated as: For each Person, grandparent = parent of parent.
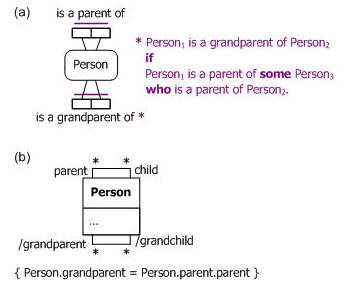
Figure 5. Deriving grandparenthood facts in (a) ORM and (b) UML.
Table 2 shows the OWL subproperty declarations for this example, in Manchester and Turtle syntax.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: isaGrandparentOf |
:isaGrandparentOf
owl:propertyChainAxiom |
If knowledge of parenthood facts is incomplete, we may wish to allow some grandparenthood facts to be simply asserted. For example, I can tell you that I am a grandparent of Emily without telling you who my children are. However, if relevant parenthood facts are known, we can derive grandparenthood for those cases. This may be modeled in ORM using a semiderived fact type for grandparenthood, as shown in Figure 6. The OWL statements in Table 2 would again be used for this situation.

Figure 6. Treating the grandparenthood fact type as semiderived in ORM.
Longer Property Chains
Property chains composed from more than two predicate occurrences are also allowed. For example, the property chain in Table 3 involves three occurrences of the parenthood predicate. The subproperty declaration enables great-grandparenthood facts to be inferred from three relevant parenthood facts. For instance, given the facts that Edward VII is a parent of George V, George V is a parent of George VI, and George VI is a parent of Elizabeth II, we may derive the fact that Edward VII is a great grandparent of Elizabeth II.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: isaGreatGrandparentOf |
:isaGreatGrandparentOf
owl:propertyChainAxiom |
In ORM and UML, the corresponding derivation rules for great-grandparenthood extend the earlier example in an obvious way. For example, the ORM derivation rule in relational style reads thus: Person1 is a great-grandparent of Person2 if Person1 is a parent of some Person3 who is a parent of some Person4 who is a parent of Person2.
As an example of a property chain involving three different predicates, consider the model shown in Figure 7, which is depicted in both ORM and UML. Here the top relationship is derived by chaining the other three relationships.
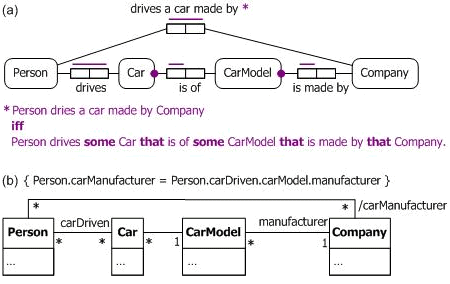
Figure 7. A derivation involving a chain of three predicates in (a) ORM and (b) UML.
The corresponding subproperty inclusion in OWL for this example is specified in Table 4, in both Manchester and Turtle syntax. This assumes that the three object properties in the chain are declared elsewhere.
Manchester Syntax |
Turtle Syntax |
ObjectProperty: drivesCarMadeBy |
:drivesCarMadeBy
owl:propertyChainAxiom |
Conclusion
The current article discussed property chains in OWL, and compared them with related features from UML and ORM. The next article examines the logical status of structural statements in OWL 2 in some depth, contrasting this with other data modeling approaches that support both integrity constraints and derivation rules.
References
[1] T.A. Halpin & T. Morgan. Information Modeling and Relational Databases, 2nd edition.
Morgan Kaufmann: San Francisco (2008). ![]()
[2] T.A. Halpin, "Ontological Modeling (Part 1)," Business Rules Journal, Vol.
10, No. 9 (Sep. 2009), URL: http://www.BRCommunity.com/a2009/b496.html ![]()
[3] T.A. Halpin, "Ontological Modeling (Part 2)," Business Rules Journal, Vol.
10, No. 12 (Dec. 2009), URL: http://www.BRCommunity.com/a2009/b513.html ![]()
[4] T.A. Halpin, "Ontological Modeling (Part 3)," Business Rules Journal, Vol.
11, No. 3 (Mar. 2010), URL: http://www.BRCommunity.com/a2010/b527.html ![]()
[5] T.A. Halpin, "Ontological Modeling (Part 4)," Business Rules Journal, Vol.
11, No. 6 (Jun. 2010), URL: http://www.BRCommunity.com/a2010/b539.html ![]()
[6] T.A. Halpin, "Ontological Modeling (Part 5)," Business Rules Journal, Vol.
11, No. 12 (Dec. 2010), URL: http://www.BRCommunity.com/a2010/b570.html ![]()
[7] T.A. Halpin, "Ontological Modeling (Part 6)," Business Rules Journal, Vol.
12, No. 2 (Feb. 2011), URL: http://www.BRCommunity.com/a2011/b579.html ![]()
[8] T.A. Halpin, "Ontological Modeling (Part 7)," Business Rules Journal, Vol.
12, No. 6 (Jun. 2011), URL: http://www.BRCommunity.com/a2011/b602.html ![]()
[9] T.A. Halpin, "Ontological Modeling (Part 8)," Business Rules Journal, Vol.
12, No. 9 (Sep. 2011), URL: http://www.BRCommunity.com/a2011/b614.html ![]()
[10] T.A. Halpin, "Ontological Modeling (Part 9)," Business Rules Journal, Vol.
12, No. 12 (Dec. 2011), URL: http://www.BRCommunity.com/a2011/b629.html ![]()
[11] Object Management Group. UML 2.0 Superstructure Specification.
Object Management Group (2003). URL: http://www.omg.org/uml ![]()
[12] Object Management Group. UML OCL 2.0 Specification.
Object Management Group (2005). URL: http://www.omg.org/spec/OCL/ ![]()
[13] W3C. OWL 2 Web Ontology Language: Primer. W3C (2009). URL: http://www.w3.org/TR/owl2-primer/
[14] W3C. OWL 2 Web Ontology Language: Direct Semantics. W3C (2009). URL: http://www.w3.org/TR/owl2-direct-semantics/
[15] W3C. OWL Web Ontology Language Manchester Syntax. W3C (2009). URL: http://www.w3.org/TR/owl2-manchester-syntax/
[16] W3C. OWL Web Ontology Language Structural Specification and Functional-Style Syntax. W3C (2009). URL: http://www.w3.org/TR/owl2-syntax/
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.











How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules