This is the third article in a series on logic-based approaches to data modeling.  The first article^[4] provided a brief overview of deductive databases and illustrated how simple data models may be declared and queried in LogiQL,^[9] a leading edge example of a deductive database system based on extended datalog.^[1]  The second article^[5] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL.  The current article explains how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.  As usual, the LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.

n-ary Fact Types with a Spanning Uniqueness Constraint

Figure 1 depicts a simple data model for recording the sports in which various countries competed in various games of the summer Olympics of the modern era.  Basic background on the graphical notations used may be found in the previous articles.  Each summer Olympics is primarily identified by its Olympiad number (rendered here for convenience in Hindu-Arabic numerals rather than the usual Latin numerals), but may also be referenced by the year for which it is assigned (whether or not it is actually held — the games for Olympiads VI, XII, and XIII were cancelled because of world wars).  For example, the first summer Olympic Games (Olympiad Number 1) of the modern era was assigned (and actually held in) the year 1896, and the most recently held summer Olympic Games (Olympiad Number XXX) was assigned the year 2012.  Figure 1(a) depicts the conceptual schema in Object-Role Modeling (ORM)^[6] notation, together with a very small sample data population.  For an extensive coverage of the relevant data, see http://en.wikipedia.org/wiki/Summer_Olympic_Games.

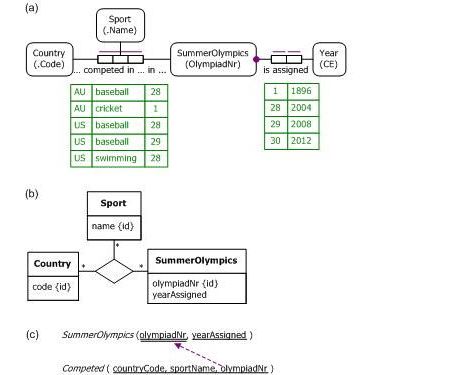
Figure 1.  Sample data model in (a) ORM, (b) UML, and (c) relational database notation.

The fact type Country competed in Sport in SummerOlympics is a ternary relationship (3-roles) with predicate reading "… competed in .. in …", where each ellipsis "…" is a placeholder for an object.  The bar spanning the three role boxes is a spanning uniqueness constraint, indicating that each triple in the fact table appears on at most one row, ensuring that each population is a set (not a bag) of rows, as is the case for all asserted fact types in ORM.  Since no stronger (shorter) uniqueness constraint applies, the fact type is a many-to-many-to-many relationship, as illustrated by the sample population, where single objects and pairs of objects may appear on more than one row.  The NORMA tool^[3] for ORM automatically verbalizes the spanning uniqueness constraints as follows:

It is possible that for some Country and Sport, that Country competed in that Sport in more than one SummerOlympics
     and that for some Country and SummerOlympics, that Country competed in more than one Sport in that SummerOlympics
     and that for some Sport and SummerOlympics, more than one Country competed in that Sport in that SummerOlympics.
In each population of Country competed in Sport in SummerOlympics,
    each Country, Sport, SummerOlympics combination occurs at most once.

The fact type SummerOlympics is assigned Year is a binary fact type (2 roles).  The solid dot on the role connection to SummerOlympics indicates that is role is mandatory for each summer Olympics.  Each role has a simple uniqueness constraint, depicted as a bar over the role, so each entry in the fact column for the role occurs on at most one row, ensuring that the fact type is a one-to-one relationship.  Collectively, the mandatory role and uniqueness constraints verbalize as follows:

Each SummerOlympics is assigned exactly one Year.
For each Year, at most one SummerOlympics is assigned that Year.

Figure 1(b) depicts the same schema as a class diagram in the Unified Modeling Language (UML)^[10] but without the sample data.  The {id} annotations indicate the identifying attributes for the classes, but UML has no graphical notation for secondary uniqueness constraints, so the uniqueness constraint that years are also identifying for summer Olympics is lost, although one could specify this constraint textually in the Object Constraint Language (OCL).^[11]  The optional, many-to-many-to-many nature of the ternary relationship is captured by the "*" (zero or more) multiplicity markers on the association ends.

The Barker notation^[2] for Entity Relationship (ER) modeling does not support n-ary relationships so is basically ignored in this article.  However, the example can be modeled indirectly in Barker ER notation by replacing the ternary relationship by a Competing entity type identified by three mandatory, many-to-one binary relationships:  one to Country, one to Sport, and one to SummerOlympics.  As with UML, Barker ER cannot capture the uniqueness constraint on the yearAssigned attribute graphically.

Figure 1(c) depicts the same data model as a relational database schema, again without the sample data.  There are two relational tables, with their candidate keys underlined.  If a table has more than one candidate key, the primary key is doubly underlined.  The arrowed line from Competed.olympiadNr to SummerOlympics.olympiadNr denotes a foreign key reference.

The schema for the example may be coded in LogiQL as shown below.  The first three lines declare the reference schemes for the entity types Country, Sport, and SummerOlympics, using string datatypes for the country codes and sport names, and integers for Olympiad numbers.  The right arrow symbol "->" stands for the material implication operator "→" of logic, and is read as "implies".  The colon ":" between the predicate arguments indicates a refmode predicate, so these predicates are injective (mandatory, 1:1).  Recall that LogiQL is case-sensitive, and each formula must end with a period.  For simplicity, years are coded as integers rather than treating them as entities with a refmode predicate.

Country(c), hasCountryCode(c:cc) -> string(cc).
Sport(s), hasSportName(s:sn) -> string(sn).
SummerOlympics(o), hasOlympiadNr(o:on) -> int(on).
competedInSportInSummerOlympics(c, s, o) -> Country(c), Sport(s), SummerOlympics(o).
yrOfSummerOlympics[o] = yr -> SummerOlympics(o), int(yr).
yrOfSummerOlympics[o1] = yr, yrOfSummerOlympics[o2] = yr  ->  o1 = o2.
SummerOlympics(o)  ->  yrOfSummerOlympics[o] = _.

The fourth line declares the n-ary predicate and constrains its types.  Since this predicate has a spanning uniqueness constraint, it is written in prefix notation with its arguments in parentheses.  Since all predicates in LogiQL are set-based, the spanning uniqueness constraint is implied, so no code is required to enforce it.

The fifth and sixth lines declare the predicate for the fact type SummerOlympics is assigned Year, and constrain it to be 1:1.  As discussed in the previous article^[5] the square bracket notation in line 5 signifies that the predicate is functional (so each summer Olympics is assigned only one year), and line six captures the other uniqueness constraint (so each year is for at most one summer Olympics).

The seventh line captures the mandatory role constraint that each summer Olympics country is assigned at least one year.  Here the underscore "_" denotes the anonymous variable, read as 'something'.  The individual variable o is implicitly universal quantified, so this formula may be read informally as follows:  Given any individual thing o, if o is a summer Olympics then its year equals something (and hence must exist).

To enter the schema in the free, cloud-based REPL tool, use a supported browser such as Chrome or Firefox to access the website, then click the "Open in new window" link to show a full screen for entering the code.  Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block.  After the "/>" prompt, type the letter 'a'.  A drop-down list of available commands starting with the letter 'a' now appears.  Click the addblock option to have the addblock command (followed by a space) added to the code window.  Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code (see Figure 2).

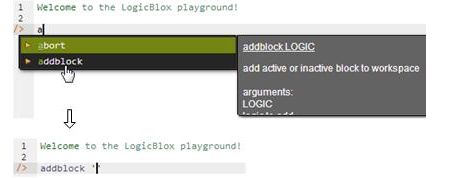
Figure 2.  Invoking the addblock command in the REPL tool.

Now copy the seven lines of schema code provided above in this article to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 3).  By default, the REPL tool also appends an automatically-generated identifier for the code block.  Alternatively, you can enter each line of code directly, using a separate addblock command for each line.

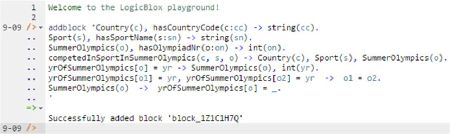
Figure 3.  Adding a block of schema code. 

The data in Figure 1(a) may be entered in LogiQL using the following delta rules.  A delta rule of the form +fact inserts that fact.  Recall that plain, double quotes (i.e., "," ) are needed here, not single quotes or smart double quotes.  Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.

+competedInSportInSummerOlympics("AU", "baseball", 28).
+competedInSportInSummerOlympics("AU", "cricket", 1).
+competedInSportInSummerOlympics("US", "baseball", 28).
+competedInSportInSummerOlympics("US", "baseball", 29).
+competedInSportInSummerOlympics("US", "swimming", 28).
+yrOfSummerOlympics[1] = 1896.
+yrOfSummerOlympics[28] = 2004.
+yrOfSummerOlympics[29] = 2008.
+yrOfSummerOlympics[30] = 2012.

There is no need to add delta rules simply to insert instances of the entity types, because those facts are implied by the constraints on the fact types.  For example, the assertion +competedInSportInSummerOlympics("AU", "baseball", 28) implies the assertions +Country("AU"), +Sport("baseball") and +SummerOlympics(28).  However, you may add those facts separately if you wish.

Delta rules to add or modify data are entered using the exec (for 'execute') command rather than the addblock command.  To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list.  A space character is automatically appended.  Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules.

Now copy the nine lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key.  A new prompt awaits your next command.  Both schema and data have now been entered (see Figure 4).

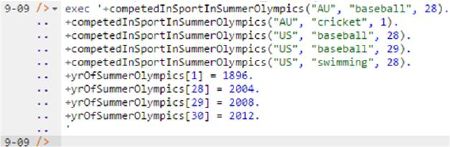
Figure 4.  Adding the data below the program code.

Now that the data model (schema plus data) is stored, you can use the print command to inspect the contents of any predicate.  For example, to list all the recorded sports, type "p" then select print from the drop-down list, and then type a space followed by "S", then select Sport from the drop-down list and press Enter.  Alternatively, type "print Sport" yourself and press Enter.  Figure 5 shows the result.  By default, the REPL tool prepends a column listing automatically generated, internal identifiers for the returned entities.

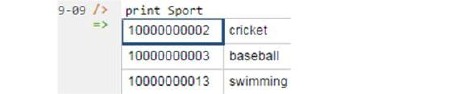
Figure 5.  Using the print command to list the extension of a predicate.

As discussed in previous articles, to perform a general query you need to specify a derivation rule to compute the facts requested by the query.  If you simply want to issue a query to derive some facts without needing to reference them later, there is no need to name the derived predicate, so we just use an anonymous predicate instead to capture the query result.  For example, using a comma "," for the logical "and" operator and an exclamation mark "!" for the logical not operator, the following query may be used to derive the Olympiad number and year of those summer Olympics for which no competing country data has yet been entered.  Here the rule's head _(o, yr) uses an anonymous predicate to capture the result derived from the rule's body.  Since the variables o and yr are head variables, they are implicitly universally quantified.  Anonymous variables for country and sport are used in the negated condition to check that there does not exist any recorded fact that a country competed in a sport for that Olympics.

_(o, yr)  <-  yrOfSummerOlympics[o] = yr, !competedInSportInSummerOlympics(_, _, o).

In LogiQL, queries are executed by appending their code in single quotes to the query command.  To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter.  The relevant query result is now displayed as shown in Figure 6.  By default, the REPL tool also prepends a column listing automatically-generated internal identifiers for the returned entities.

Figure 6.  Using the query command to execute a sample query. 

n-ary Fact Types with Internal Uniqueness Constraints spanning n-1 Roles

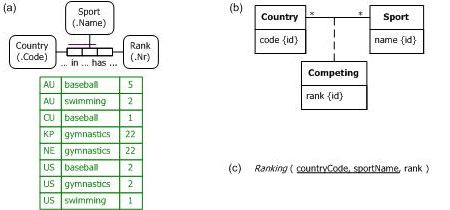
Figure 7.  Another sample data model in (a) ORM, (b) UML, and (c) relational database notation.

As indicated earlier, predicates in LogiQL are by default assumed to have a spanning uniqueness constraint.  In practice, most n-ary predicates are constrained by one or more uniqueness constraints, each of which spans n-1 roles.  ORM requires asserted fact types to be atomic, so uniqueness constraints spanning fewer than n-1 roles are not allowed.  For example, a ternary fact type with a single-role uniqueness constraint is not atomic as it can be split into a conjunction of shorter fact types.

Figure 7 depicts a simple data model for recording the ranks of various countries in various sports, based on their collective medal tally over all the modern summer Olympics.  The ORM data model in Figure 7(a) includes a small, sample data population.  For an extensive coverage of the relevant data, see http://en.wikipedia.org/wiki/Summer_Olympic_Games.  These Olympic sport rankings allow ties.  For example, in Figure 7(a) both North Korea (country code = KP) and the Netherlands (country code = NE) are ranked 22nd in gymnastics.  The ORM schema comprises a ternary fact type with a uniqueness constraint spanning just its first two roles, so no duplicate (country, sport) pairs are allowed in its fact table.  This constraint verbalizes thus:  For each Country and Sport, that Country in that Sport has at most one Rank.

Figure 7(b) shows one way to model this example in UML, using an association to capture which countries competed in which sports, and forming a class from this association to which the rank is attached as an attribute.  Figure 7(c) models the example in relational database notation, with the primary key underlined.

Like ORM, LogiQL models all facts using predicates, not attributes, so this example is modeled using a ternary predicate to record the rank of a country in a sport.  Since Country and Sport have already been declared, there is no need to declare them again.  Again for simplicity, ranks are typically modeled as integers.  Since rank is a function of the country and sport combination, this is an example of a functional, n-ary fact type.  Hence the square bracket notation is used to declare this functionality, as shown in the following LogiQL code.

rankOfCountryInSport[c, s] = r  ->  Country(c), Sport(s), int(r).

To implement this in the REPL tool, use the add block command and copy the above code in the usual way, as shown in Figure 8.

Figure 8.  Adding the schema for Figure 7 in the REPL tool.

The sample data in Figure 7 may be added using the following delta rules:

+rankOfCountryInSport["AU", "baseball"] = 5.
+rankOfCountryInSport["AU", "swimming"] = 2.
+rankOfCountryInSport["CU", "baseball"] = 1.
+rankOfCountryInSport["KP", "gymnastics"] = 22.
+rankOfCountryInSport["NE", "gymnastics"] = 22.
+rankOfCountryInSport["US", "baseball"] = 2.
+rankOfCountryInSport["US", "gymnastics"] = 2.
+rankOfCountryInSport["US", "swimming"] = 1.

To implement this in the REPL tool, use the exec command and copy the above code in the usual way, as shown in Figure 9.

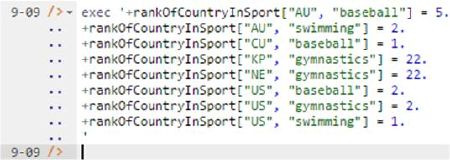
Figure 9.  Adding the data for Figure 7 in the REPL tool.

You can now print and query the model in the usual way.  For example, the following query lists each country and sport where that country is ranked second in that sport.

_(c, s)  <-  rankOfCountryInSport[c, s] = 2.

For the limited data provided, this query yields the following result.  Here, artificial ids are prepended by default for both countries and sports, since both are modeled as entities.

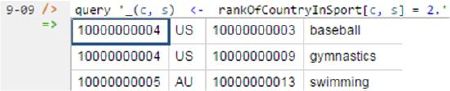
Figure 10.  Using the query command to execute a sample query.

Overlapping Uniqueness Constraints and Mandatory Role Constraints on n-ary Fact Types

Now suppose that the rating system is changed so that no ties are allowed.  For example, suppose some new criterion is added that enables the Netherlands to be ranked in gymnastics just ahead (rank 22) of North Korea (rank 23), as shown in the ORM model population in Figure 11(a).  To ensure that no ties are allowed, an additional uniqueness constraint is applied on the pair of roles hosted by Sport and Rank, so no duplicate (sport, rank) pairs are allowed in its fact table.  This constraint verbalizes as follows:  For each Sport and Rank, at most one Country in that Sport has that Rank.

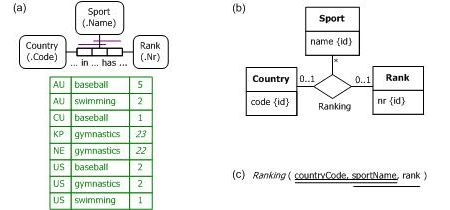
Figure 11.  A modified example where no ties are allowed, modeled in (a) ORM, and (b) relational database notation.

The UML class diagram in Figure 7(b) modeled rank as an attribute, so can't be extended with a graphical constraint to enforce the no-ties constraint.  However, this constraint can be captured graphically in UML by modeling Rank as a class and using a ternary association for Ranking, as shown in Figure 11(b).  The two uniqueness constraints are now captured by the 0..1 multiplicity constraints.

The relational database model shown in Figure 11(c) captures the uniqueness constraint over (country, sport) pairs as a primary key constraint (shown here with a double-underline).  The uniqueness constraint over (sport, rank) pairs is captured by a secondary key constraint (shown here with single-underline).

The easiest way to update North Korea's rank in gymnastics from 22 to 23 is to execute the following upsert rule.  The circumflex "^" modifier for upserts is used instead of the "+" and "-" modifiers which are used respectively for insertion and deletion.  As the name "upsert" suggests, this may be used to either update or insert.  If the key (in square brackets) of the functional fact already exists, its functionally determined value is updated, as in this example.  Otherwise the fact is simply inserted.

^rankOfCountryInSport["KP", "gymnastics"] = 23.

A longer but equivalent way to perform the update is to first delete the existing fact and then insert the new fact that replaces it, as shown below:

-rankOfCountryInSport["KP", "gymnastics"] = 22.
+rankOfCountryInSport["KP", "gymnastics"] = 23.

Note that the upsert shortcut may be used only with functional predicates.  To execute this update in the REPL tool, invoke the exec command and enter the command in the usual way (see Figure 12).

Figure 12.  Executing an update in the REPL tool.

In LogiQL, the uniqueness constraint over (sport, rank) pairs may be declared as follows.  This says that if any countries c1 and c2 in the same sport s have the same rank r, then c1 and c2 must be the same country.

rankOfCountryInSport[c1, s] = r,  rankOfCountryInSport[c2, s] = r  ->  c1 = c2.

Figure 13.  Adding the no-ties constraint in the REPL tool. 

Now suppose that we extend the model by requiring each recorded country to have a name and a sport rating.  Figure 14(a) shows how to do this in ORM by adding the 1:1 fact type Country has CountryName and applying mandatory role constraints to the roles hosted by Country.  Modeling and coding of the country name fact type was discussed in the previous article.^[10]  The mandatory role constraint on Country's role in the ternary fact type verbalizes as follows:  Each Country in some Sport has some Rank.

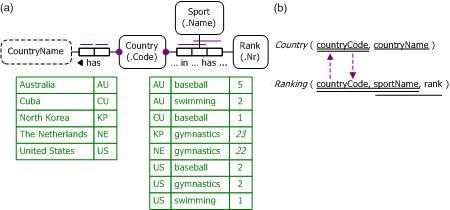
Figure 14.  Extending the previous model in (a) ORM, and (b) relational database notation.

Although multiplicity constraints in UML work well with binary associations, they often have limited expressive power when n-ary associations are used.  For example, there is no way to express the mandatory role constraint on the ternary association as a graphical constraint in UML.  So we ignore UML for this extended example.  For further details about multiplicities on n-aries in UML, see [10, p. 362].

Figure 14(a) models the example in relational database notation, using dashed-arrows to depict subset constraints.  The upward arrow may be declared as a foreign key constraint, but the downward arrow needs separate code (e.g., using triggers) to enforce the mandatory role constraint under discussion.

We now discuss how to code the extensions to the model in LogiQL.  The functional, country name fact type may be declared as follows.

countryNameOf[c] = cn  ->  Country(c), string(cn).

and entered as a block in the usual way in REPL (see Figure 15).

Figure 15.  Adding the country name fact type in the REPL tool.

We now populate this fact type with the extra data in Figure 14 in the usual way by executing five fact insertions (see Figure 16).

Figure 16.  Adding the names of countries in the REPL tool.

The inverse functional nature of the country name predicate is declared by the first line of code below.  The next two lines of code declare the mandatory role constraints on Country, with the final line enforcing the mandatory role constraint on the ternary, ensuring that each country has some rank in some sport.

countryNameOf[c1] = cn, countryNameOf[c2] = cn  ->  c1 = c2.
Country(c)  ->  countryNameOf[c] = _.
Country(c)  ->  rankOfCountryInSport[c, _] = _.

This block of code may now be added in REPL tool in the usual way (see Figure 17).

Figure 17.  Adding the country name fact type in the REPL tool. 

That completes the entry of the model extensions.  The model may now be queried in the usual way.  For example, the following query will return, for each recorded sport, the rank and name of those countries that are recorded to rank first or second in that sport.

_(s, r, cn)  <-  rankOfCountryInSport[c, s] = r, r <= 2, countryNameOf[c] = cn.

Running this query in REPL tool yields the result shown in Figure 18.  As usual, internal identifiers are prepended for the returned entities (in this case, sports — recall that we chose to code ranks and country names in LogiQL as data values rather than entities).

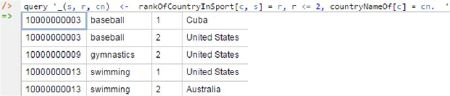
Figure 18.  Using the query command to execute a sample query on the extended data model. 

Conclusion

The current article discussed how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.  Future articles in this series will examine how LogiQL can be used to specify business constraints and rules of a more advanced nature.  For readers interested in a fuller treatment of the language, a new book^[7] has just been published which provides an in-depth coverage of LogiQL.

References

[1]  S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995).  

[2]  R. Barker, CASE*Method:  Entity Relationship Modelling, Addison-Wesley:  Wokingham, England (1990).  

[3]  M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2, "P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204.  

[4]  T.A. Halpin, "Logical Data Modeling (Part 1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL:  http://www.BRCommunity.com/a2014/b760.html  

[5]  T.A. Halpin, "Logical Data Modeling (Part 2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL:  http://www.BRCommunity.com/a2014/b780.html  

[6]  T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann:  San Francisco (2008).  

[7]  T.A. Halpin & S. Rugaber, LogiQL:  A Query language for Smart Databaseson, CRC Press:  Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939#  

[8]  T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.  

[9]  S. Huang, T. Green, & B. Loo, "Datalog and emerging applications:  an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011).  At:  http://dl.acm.org/citation.cfm?id=1989456  

[10]  Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013).  Available online at:  http://www.omg.org/spec/UML/2.5/  

[11]  Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1.  Object Management Group (2012).  Retrieved from http://www.omg.org/spec/OCL/2.3.1/  

# # #