Logical Data Modeling (Part 4)
This is the fourth article in a series on logic-based approaches to data modeling. The first article[5] provided a brief overview of deductive databases and illustrated how simple data models may be declared and queried in LogiQL,[2], [10], [12] a leading edge deductive database language based on extended datalog.[1] The second article[6] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL. The third article[7] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them.
The current article discusses how to declare external uniqueness constraints in LogiQL. The LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.
External Uniqueness Constraints
Table 1. Extract from a report on presidents of the United States.
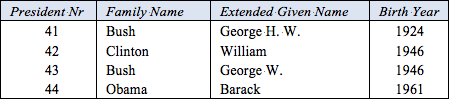
Table 1 shows an extract from a report about presidents of the United States. Here, US presidents are primarily identified by their president number, which indicates their position in a list of all US presidents, ordered by the date of their inauguration as president. For the full list of US presidents, see http://en.wikipedia.org/wiki/List_of_Presidents_of_the_United_States. US presidents can also be identified by the combination of their family name and extended given name. An extended given name is a given name, possibly extended by one or more initials or numbers to provide a distinct full-name for each person. Figure 1 schematizes this example as (a) an Object-Role Modeling (ORM)[8], [9] diagram, (b) an Entity Relationship diagram in Barker notation (Barker ER),[3] (c) a class diagram in the Unified Modeling Language (UML),[13] and (d) a relational database (RDB) schema.
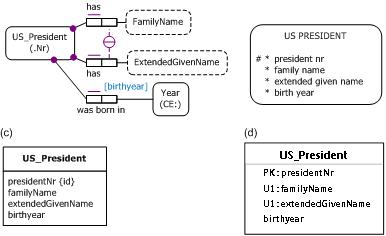
Figure 1. Data model for Table 1 in (a) ORM, (b) Barker ER, (c) UML, and (d) relational database notation.
The ORM schema in Figure 1(a) displays three internal uniqueness constraints (shown as a bar over the constrained role) and three mandatory role constraints (shown as a solid dot). The preferred reference scheme for US_President is depicted by the popular reference mode "Nr" shown in parentheses. The circled, uniqueness bar connected by dashed lines to the roles hosted by FamilyName and ExtendedGivenName depicts an external uniqueness constraint, which underlies the secondary reference scheme for US_President. The NORMA tool[4] for ORM automatically verbalizes this external uniqueness constraint as follows:
For each FamilyName and ExtendedGivenName,
at most one US_President has that FamilyName and has that ExtendedGivenName.
The Barker ER schema in Figure 1(b) depicts the primary reference scheme for US_President by prepending an octothrope "#" to the president nr attribute. The Barker ER graphical notation does not support secondary reference schemes, but the equivalent of ORM's external uniqueness constraint may be documented textually in an entity definition form (see Appendix C of [3]).
The UML class diagram in Figure 1(c) depicts the primary identification for US_President by appending "{id}" to the presidentNr attribute. The UML graphical notation does not support secondary identification schemes, but the equivalent of ORM's external uniqueness constraint may be documented textually as a formula in its Object Constraint Language (OCL).[14]
Figure 1(d) shows the relational database schema diagram generated by the NORMA tool[4] from the ORM schema. Here, the primary reference scheme for US_President is indicated by prepending "PK" (for "Primary Key) to the presidentNr attribute. The composite uniqueness constraint over the familyName and extendedGivenName attributes is depicted by prepending "U1" (for Uniqueness constraint 1) to those attributes.
The schema for the example may be coded in LogiQL as shown below. The right arrow symbol "->" stands for the material implication operator "→" of logic, and is read as "implies". Recall that LogiQL is case-sensitive, and each formula must end with a period. The colon ":" in hasPresidentNr(p:pn) distinguishes hasPresident as a refmode predicate, so this predicate is injective (mandatory, 1:1). For simplicity, years are coded as integers rather than treating them as entities with a refmode predicate.
The first line declares US_President as an entity type whose instances may be referenced by president numbers which are coded as integers. The next three lines declare the typing constraints on the family name, extended give name, and birth year predicates, using the square bracket syntax to declare that these predicates are functional (many-to-one). The next formula declares three mandatory role constraints. (The underscore "_" depicts an anonymous variable, and is read as "something".)
US_President(p), hasPresidentNr(p:pn) -> int(pn).
familyNameOf[p] = fn -> US_President(p), string(fn).
extendedGivenNameOf[p] = egn -> US_President(p), string(egn).
birthyearOf[p] = yr -> US_President(p), int(yr).
US_President(p) -> familyNameOf[p] = _, extendedGivenNameOf[p] = _, birthyearOf[p] = _.
familyNameOf[p1] = fn, extendedGivenNameOf[p1] = egn,
familyNameOf[p2] = fn, extendedGivenNameOf[p2] = egn -> p1 = p2.
The final formula declares the external uniqueness constraint. The individual variables p1 and p2 are implicitly universally quantified, so this formula may be read informally as follows:
Given any individual things p1 and p2, if the family name of p1 is fn, and the extended given name of p1 is egn, and the family name of p2 is fn, and the extended given name of p2 is egn, then p1 must be identical to p2.
To enter the schema in the free, cloud-based REPL tool, use a supported browser such as Chrome or Firefox to access the website (https://developer.logicblox.com/playground/), then click the "Open in new window" link to show a full screen for entering the code. Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block. After the "/>" prompt, type the letter "a". A drop-down list of available commands starting with the letter "a" now appears. Click the addblock option to have the addblock command (followed by a space) added to the code window. Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code (see Figure 2).
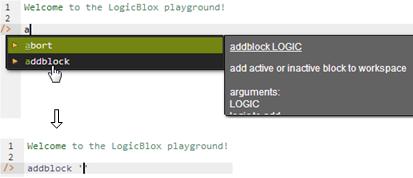
Figure 2. Invoking the addblock command in the REPL tool.
Now copy the seven lines of schema code provided above in this article to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 3). By default, the REPL tool also appends an automatically generated identifier for the code block. Alternatively, you can enter each line of code directly, using a separate addblock command for each line.
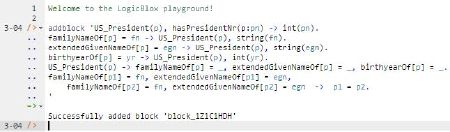
Figure 3. Adding a block of schema code.
The data in Table 1 may be entered in LogiQL using the following delta rules. A delta rule of the form +fact inserts that fact. Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes. Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.
+familyNameOf[41] = "Bush", +extendedGivenNameOf[41] = "George H. W.", +birthyearOf[41] = 1924.
+familyNameOf[42] = "Clinton", +extendedGivenNameOf[42] = "William", +birthyearOf[42] = 1946.
+familyNameOf[43] = "Bush", +extendedGivenNameOf[43] = "George W.", +birthyearOf[43] = 1946.
+familyNameOf[44] = "Obama", +extendedGivenNameOf[44] = "Barack", +birthyearOf[44] = 1961.
There is no need to add delta rules simply to insert instances of the entity type US_President, because those facts are implied by facts in which they participate. For example, the assertion +familyNameOf[41] = "Bush" implies the assertion +US_President(41). However, you may add those facts separately if you wish.
Delta rules to add or modify data are entered using the exec (for 'execute') command rather than the addblock command. To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list. A space character is automatically appended. Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules.
Now copy the lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. A new prompt awaits your next command. Both schema and data have now been entered (see Figure 4).

Figure 4. Adding the data below the program code.
Now that the data model (schema plus data) is stored, you can use the print command to inspect the contents of any predicate. For example, to list all the recorded US presidents, type "p" then select print from the drop-down list, and then type a space followed by "U", then select US_President from the drop-down list and press Enter. Alternatively, type "print US_President" yourself and press Enter. Figure 5 shows the result. By default, the REPL tool prepends a column listing automatically generated, internal identifiers for the returned entities.
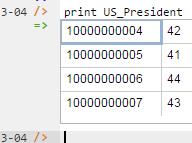
Figure 5. Using the print command to list the extension of a predicate.
As discussed in previous articles, to perform a general query, you need to specify a derivation rule to compute the facts requested by the query. If you simply want to issue a query to derive some facts without needing to reference them later, there is no need to name the derived predicate, so we just use an anonymous predicate instead to capture the query result. For example, using a comma "," for the logical "and" operator, the following query may be used to list the family name and extended given name of those US presidents who were born in the year 1946. Here the rule's head _(fn, egn) uses an anonymous predicate to capture the result derived from the rule's body. Since the variables fn and egn are head variables, they are implicitly universally quantified. The variable p is introduced in the body, so is implicitly existentially quantified.
_(fn, egn) <- familyNameOf[p] = fn, extendedGivenNameOf[p] = egn, birthyearOf[p] = 1946.
In LogiQL, queries are executed by appending their code in single quotes to the query command. To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter. The relevant query result is now displayed as shown in Figure 6.

Figure 6. Using the query command to execute a sample query.
Now consider the modified report extract shown in Table 2. This report does not identify presidents by their president number, so the only way to identify the presidents is use the combination of their family name and extended given name.
Table 2. Extract from a report on presidents of the United States, identifying the presidents only by their full name.
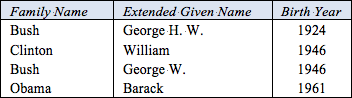
Figure 7 models this new example as (a) an ORM diagram, (b) a Barker ER diagram, (c) a UML class diagram, and (d) an RDB schema. The ORM diagram in Figure 7(a) uses a double uniqueness bar rather than a single uniqueness bar for the external uniqueness constraint to indicate that this external uniqueness constraint underlies the preferred reference scheme for US President. The Barker ER schema in Figure 7(b) depicts this composite reference scheme by prepending an octothrope "#" to the family name and extended give name attributes. The UML class diagram in Figure 7(c) depicts this composite identification scheme by appending "{id}" to the familyName and extendedGivenName attributes. The relational schema diagram in Figure 7(d) generated by NORMA from the ORM schema indicates the composite primary key by prepending "PK" to the familyName and extendedGivenName attributes.
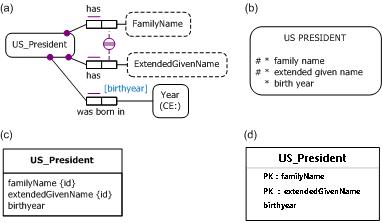
Figure 7. Data model for Table 2 in (a) ORM, (b) Barker ER, (c) UML, and (d) relational database notation.
One attempt to model Table 2 in LogiQL is to simply structure it as a many-to-many-to-one, ternary relationship, as shown below.
// schema
birthYearOfUS_presidentNamed[fn, egn] = yr -> string(fn), string(egn), int(yr).
//data
+birthYearOfUS_PresidentNamed["Bush", "George H. W."] = 1924.
+birthYearOfUS_PresidentNamed["Clinton", "William"] = 1946.
+birthYearOfUS_PresidentNamed["Bush", "George W."] = 1946.
+birthYearOfUS_PresidentNamed["Obama", "Barack"] = 1961.
The data may then be retrieved using the following query:
_(fn, egn, yr) <- birthYearOfUS_PresidentNamed[fn, egn] = yr.
However, this leaves the existence of actual US presidents implicit. Moreover, it fails to capture the external uniqueness constraint to ensure that each combination of family name and extended given name applies to only one US president. To avoid these problems, we explicitly derive the existence of US presidents from combinations of their family name and extended given name by using a constructor. LogiQL requires that each entity type be identified using either a refmode predicate or a constructor. In this case, US_President has no reference mode so a constructor for it is declared as n in the following code.
US_President(p) -> .
US_PresidentNamed[fn, egn] = p -> string(fn), string(egn), US_President(p).
lang:constructor(`US_PresidentNamed).
pairsWith(fn, egn) -> string(fn), string(egn).
US_President(p), US_PresidentNamed[fn, egn] = p <- pairsWith(fn, egn).
birthyearOf[p] = yr -> US_President(p), int(yr).
US_President(p) -> birthyearOf[p] = _.
birthyearOf[p] = 1924 <- US_PresidentNamed["Bush", "George H. W."] = p.
birthyearOf[p] = 1946 <- US_PresidentNamed["Clinton", "William"] = p.
birthyearOf[p] = 1946 <- US_PresidentNamed["Bush", "George W."] = p.
birthyearOf[p] = 1961 <- US_PresidentNamed["Obama", "Barack"] = p.
The first line declares that US_President is an entity type with no reference mode (i.e., it is a refmodeless entity type). The second line types the arguments of the functional US_PredicateNamed predicate. The third line declares that this predicate is a constructor for its functionally-determined result (the entity type US_President). Moreover, the constructor declaration constrains the mapping from (fn, egn) pairs to US president entities to be 1:1, so the external uniqueness constraint is now enforced.
The fourth formula declares the pairsWith predicate, allowing us to assert which family names are combined with which extended given names. The fifth formula is a derivation rule that derives the existence of US presidents from asserted family name and extended given name combinations. In classical datalog, variables in the head of rule are assumed to be universally quantified. As an extension beyond classical datalog, LogiQL treats an entity type variable in the head of a rule to be existentially quantified if the entity type is refmodeless and has a constructor-based reference scheme. So this rule may be read as follows:
For each fn and egn, there exists a US president p who is named by fn and egn if fn is paired with egn.
Because the individual variable p is existentially quantified in the head of the derivation rule, it is called a head existential. Head existential variables cannot be used in the body of the rule. US_President is called a derived entity type since its instances are derived by means of a derivation rule.
The sixth formula types the functional birth year predicate in the usual way. The seventh formula declares the mandatory role constraint on the birth year predicate. Since no other constructors are provided for US_President, the mandatory role constraints to ensure that each US president have fn and egn names are implied. The last four formulae are rules to derive (rather than assert) the birth year facts.
The pairing of family name and extended given names needs to be asserted as data as shown below.
+pairsWith("Bush", "George H. W.").
+pairsWith("Clinton", "William").
+pairsWith("Bush", "George W.").
+pairsWith("Obama", "Barack").
If you add the above schema and data to the REPL tool in the usual way, you may use the following query to display the presidential data.
_(p, fn, egn, byr) <- US_PresidentNamed[fn, egn] = p, birthyearOf[p] = byr.
Figure 8 shows the query result. Artificial ids are included for the presidents since these were modeled as entities. Further details on derived entities may be found in [10, Unit 4.3], which also covers a similar example to the one discussed here.

Figure 8 Querying the new version of the sample data model.
Table 3. Extract from a report on countries and politicians.
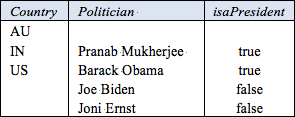
As a final example of external uniqueness constraints, consider the report extract shown in Table 1, which is adapted from an example in [8]. Here, countries are identified by their country code, and politicians are identified simply by a single name. It is optional whether to record any politicians for a country. If a politician is recorded we must record which country is served by that politician, and may record whether that politician is a president. Each country has at most one politician as president.
Figure 9(a) models this example as a populated ORM schema. Here, the external uniqueness constraint is called a unique-where-true constraint and applies only when the unary fact type Politician is a president is populated. The NORMA tool verbalizes this constraint as follows:
For each Country,
at most one Politician is a president
and serves that Country.
Figure 9(b) displays the relational schema diagram generated by NORMA from the ORM schema. The composite uniqueness constraint over the countryCode and isAPresident attributes applies only where the value of isAPresident equals true. Neither Barker ER nor UML can capture this constraint in their graphical notation, and diagrams those modeling approaches are omitted.
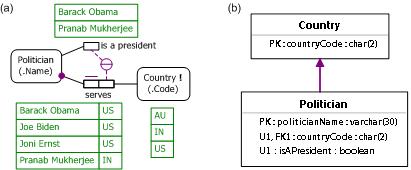
Figure 9. A data model for Table 3 displayed as (a) an ORM model, and (b) a relational schema.
The schema may be coded in LogiQL as shown below. The final formula captures the unique-where-true constraint.
Politician(p), hasPoliticanName(p:pn) -> string(pn).
Country(c), hasCountryCode(c:cc) -> string(cc).
isaPresident(p) -> Politician(p).
countryServedBy[p] = c -> Politician(p), Country(c).
Politician(p) -> countryServedBy[p] = _.
isaPresident(p1), countryServedBy[p1] = c, isaPresident(p2), countryServedBy[p2] = c -> p1 = p2.
The data may be entered using the following delta rules.
+Country("AU").
+isaPresident("Barack Obama").
+isaPresident("Pranab Mukherjee").
+countryServedBy["Barack Obama"] = "US".
+countryServedBy["Joe Biden"] = "US".
+countryServedBy["Joni Ernst"] = "US".
+countryServedBy["Pranab Mukherjee"] = "IN".
If you add the above schema and data to the REPL tool in the usual way, you may use the following query to display the names and country served by each president.
_(p, c) <- countryServedBy[p] = c, isaPresident(p).
For the limited data provided, this query yields the following result. Artificial ids are prepended by default for both politicians and countries since both are modeled as entities.

Figure 10. Querying for the names and countries served by each president in the REPL tool.
Conclusion
The current article discussed how to declare external uniqueness constraints in LogiQL, covering the three cases where the constraint is used for a preferred composite identifier, a secondary composite identifier, or as a unique-where-true constraint. Future articles in this series will examine how LogiQL can be used to specify business constraints and rules of a more advanced nature. Further coverage of LogiQL may be found in [10].
References
[1] S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995). ![]()
[2] M. Aref, B. Cate, T. Green, B. Kimefeld, D. Olteanu, E. Pasalic, T. Veldhuizen, & G. Washburn, "Design and Implementation of the LogicBlox System," Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York (2015). http://dx.doi.org/10.1145/2723372.2742796 ![]()
[3] R. Barker, CASE*Method: Entity Relationship Modelling, Addison-Wesley: Wokingham, England (1990). ![]()
[4] M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2," P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204. ![]()
[5] T.A. Halpin, "Logical Data Modeling (Part
1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL: http://www.BRCommunity.com/a2014/b760.html ![]()
[6] T.A. Halpin, "Logical Data Modeling (Part
2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL: http://www.BRCommunity.com/a2014/b780.html ![]()
[7] T.A. Halpin, "Logical Data Modeling (Part
3)," Business Rules Journal, Vol. 16, No. 1 (Jan. 2015), URL: http://www.BRCommunity.com/a2015/b795.html ![]()
[8] T.A. Halpin, Object-Role Modeling Fundamentals, Technics Publications: New Jersey (2015). ![]()
[9] T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann: San Francisco (2008). ![]()
[10] T.A. Halpin & S. Rugaber, LogiQL: A Query language for Smart Databases, CRC Press: Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939# ![]()
[11] T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.
[12] S. Huang, T. Green, & B. Loo, "Datalog and emerging applications: an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011). At: http://dl.acm.org/citation.cfm?id=1989456 ![]()
[13] Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013). Available online at: http://www.omg.org/spec/UML/2.5/ ![]()
[14] Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1, Object Management Group (2012). Retrieved from http://www.omg.org/spec/OCL/2.3.1/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules