Logical Data Modeling (Part 7)
This is the seventh article in a series on logic-based approaches to data modeling. The first article[5] briefly overviewed deductive databases and illustrated how simple data models with asserted and derived facts may be declared and queried in LogiQL,[2], [14], [16] a leading-edge deductive database language based on extended datalog.[1] The second article[6] discussed how to declare inverse predicates, simple mandatory role constraints, and internal uniqueness constraints on binary fact types in LogiQL. The third article[7] explained how to declare n-ary predicates and apply simple mandatory role constraints and internal uniqueness constraints to them. The fourth article[8] discussed how to declare external uniqueness constraints in LogiQL. The fifth article[9] covered derivation rules in a little more detail and showed how to declare inclusive-or constraints. The sixth article[10] discussed how to declare simple set-comparison constraints (i.e. subset, exclusion, and equality constraints), and exclusive-or constraints.
The current article explains how to declare subset constraints between compound role sequences, including cases involving join paths. The LogiQL code examples are implemented using the free, cloud-based REPL (Read-Eval-Print-Loop) tool for LogiQL that is accessible at https://developer.logicblox.com/playground/.
Compound Subset Constraints without Join Paths
Table 1 shows extracts from reports containing data about students, courses, student enrolments, and the grades obtained (if known) for those enrolments. A blank entry for a grade indicates that the course has not been completed by the student. Students are identified by their student number and also have a name (not necessarily unique). Courses are primarily identified by their course code, but also have unique titles. Grades are identified by a letter. A student may be recorded without enrolling in any course (e.g., student 103 may enroll in a program (not shown here) before choosing courses). Some courses on offer might have no enrollments yet (e.g., CS400). As an optional exercise, you might like to specify a data model for this example, including all relevant constraints, before reading on.
Table 1. Report extracts of data about students, courses, course enrolments, and grades obtained (if known).
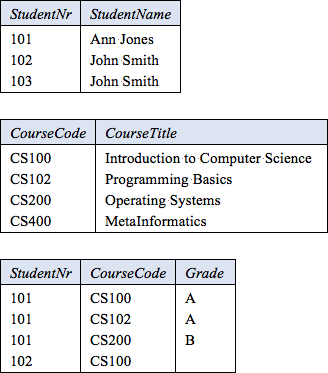
Figure 1 models this example with a populated Object-Role Modeling (ORM)[11], [12], [13] diagram. The sample facts are shown in fact tables next to the relevant fact types. The preferred reference schemes for Student and Course are depicted by the popular reference modes ".Nr" and ".Code" shown in parentheses.
The mandatory role dot and uniqueness constraint bar on Student's role in the fact type Student has StudentName indicates that each student has exactly one student name. The absence of a uniqueness constraint bar on the role hosted by StudentName indicates that more than one student may have the same name. The mandatory role and uniqueness constraints on the fact type Course has CourseCode indicate that each course has exactly one course title, and each course title applies to only one course. The uniqueness constraint bar spanning both roles of the binary fact type Student enrolled in Course indicates that the relationship is many-to-many. The uniqueness constraint bar spanning the first two roles of the ternary fact type Student for Course got Grade indicates that the relationship is many-to-many-to-one.
If a role connector meets the junction of adjacent roles, it applies to the role pair. So in this model the subset constraint depicted using a circled subsethood operator "⊆" is directed from the first two roles of the ternary fact type to the role pair in the binary fact type. This subset constraint indicates that the set of (student, course) pairs that populate the ternary grade predicate must be a subset of the (student, course) pairs that populate the enrollment predicate.
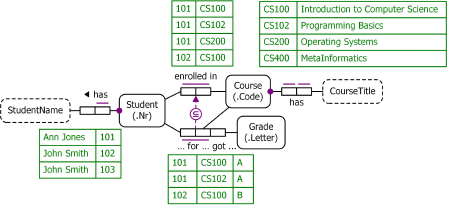
Figure 1. Populated data model for Table 1 in ORM notation.
The NORMA tool[4] verbalizes this subset constraint as follows:
For each Student and Course,
if that Student for that Course got some Grade
then that Student enrolled in that Course.
A subset constraint between role-pairs is sometimes called a pair-subset constraint. This is the most common kind of subset constraint. In general, a subset constraint may apply between two compatible sequences of one or more roles. Two role sequences are compatible if their corresponding roles are based on the same type.
If a constrained role sequence is comprised of noncontiguous roles or at least three roles, multiple connectors are used to indicate the role sequence. For example, the subset constraint in Figure 2(a) is directed from the role-pair comprising the first and third role of the lower predicate to the role-pair comprising the first and third roles of the upper predicate. The subset constraint in Figure 2(b) is directed from the role-triple comprising the first three roles of the lower predicate to the role-triple comprising the upper predicate.
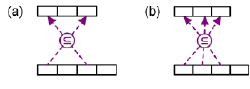
Figure 2. Example subset constraints involving non-contiguous role sequences or sequences of more than two roles.
Our later discussion of coding the model in LogiQL is based on the ORM model in Figure 1. The ORM schema for this model is repeated in Figure 3(a). An alternative way to model the same universe of discourse in ORM is to explicitly introduce Enrolment as a coreferenced entity type, with a composite reference scheme based on its relationships to Student and Course, as shown in Figure 3(b). Yet another way to model Table 1 in ORM is to objectify the enrolment relationship as Enrolment, as shown in Figure 3(c). As the enrolment relationship in Figure 3(b) is displayed nested inside the Enrolment object type, this is said to be a nested approach, unlike the "flattened" approach of Figure 3(a). In each of the coreferenced and nested alternatives, Enrolment is declared to be independent (as depicted by the appended exclamation mark), thus allowing an enrolment to be recorded without a grade.
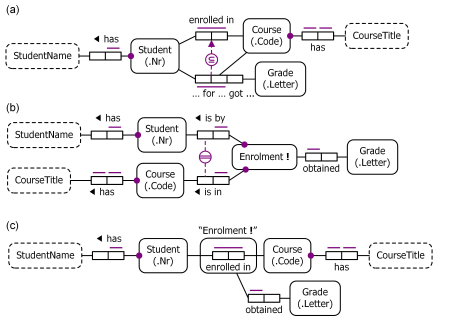
Figure 3. Equivalent ORM schemas for Table 1 in (a) flattened, (b) coreferenced, and (c) nested forms.
ORM's formalization in logic enables formal proofs that the three schemas in Figure 3 are conceptually equivalent. However, ORM's relational mapping (Rmap) procedure generates four tables for the flattened ORM schema and three tables for the coreferenced and nested versions. For typical applications, the three table relational schema is more efficient. ORM's conceptual schema optimization procedure[13] recommends transforming the flattened version into the coreferenced or nested version before relational mapping, thus resulting in the more efficient relational schema generated by the NORMA tool[4] as shown in Figure 4.

Figure 4. Relational schema obtained by mapping the ORM schema in Figure 3(b) or Figure 3(c).
In the relational schema diagram, table names are displayed at the top, with attributes below. The primary key (simple or composite) of a table is denoted by "PK"; foreign key attributes are denoted by "FKn" with the foreign key dependencies depicted as arrows. Non-nullable attributes are displayed in bold, so gradeLetter is the only optional attribute. For a more compact diagram, display of data types has been suppressed.
Figure 5(a) schematizes the same universe of discourse depicted in Table 1 as an Entity Relationship diagram in Barker notation (Barker ER).[3] The Barker ER schema depicts the primary reference scheme for Student and Course by prepending an octothorpe "#" to the student nr and course code attributes respectively. The asterisk "*" prepended to the student nr, student name, course code, and course title attributes indicates that these attributes are mandatory. The small "o" prepended to the grade attribute indicates that this attribute is optional. The half-solid, half-dashed lines indicate that the binary relationships are mandatory for Enrolment and optional for Student and Course. A crowsfoot at only the Enrolment end of the relationship lines indicates that the relationships are many-to-one. The stroke "|" through both the relationship lines indicates that these two relationships provide the primary reference scheme for Enrolment. Barker ER has no graphical way to display secondary keys, so the uniqueness of course titles is not captured in the diagram.
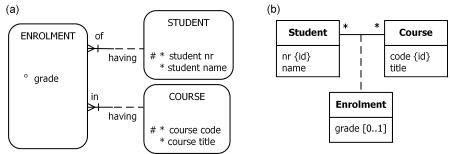
Figure 5. Data schema for Table 1 in (a) Barker ER, and (b) UML notation.
Figure 5(b) schematizes Table 1 as a class diagram in the Unified Modeling Language (UML).[17] The UML class diagram depicts the primary identification for Student and Course by appending "{id}" to the nr and code attributes respectively. The nr, name, code, and title attributes by default have a multiplicity of 1, so are mandatory and single-valued. The multiplicity asterisks at the end of the enrolment association indicate that it is optional on both sides and many-to-many. The dashed line from the Enrolment class to this association indicates that Enrolment is the objectification of that association. The [0..1] multiplicity constraint shown on the grade attribute of Enrolment indicates that this attribute is optional and has a maximum multiplicity of 1. Like Barker ER, UML has no way to display graphically that course titles are unique.
The Figure 3(a) ORM schema may be coded in LogiQL as shown below. The right arrow symbol "->" stands for the material implication operator "→" of logic, and is read as "implies". A comma "," denotes the logical conjunction operator "&" and is read as "and". Recall that LogiQL is case-sensitive, each formula must end with a period, and head variables are implicitly universally quantified.
Student(s), hasStudentNr(s:n) -> int(n).
Course(c), hasCourseCode(c:cc) -> string(cc).
Grade(g), hasGradeLetter(g:gl) -> string(gl).
studentNameOf[s] = sn -> Student(s), string(sn).
courseTitleOf[c] = ct -> Course(c), string(ct).
enrolledIn(s, c) -> Student(s), Course(c).
gradeOfStudentInCourse[s, c] = g ->
Student(s), Course(c), Grade(g).
// Each student has a name
Student(s) -> studentNameOf[s] = _.
// Each course has a title
Course(c) -> courseTitleOf[c] = _.
// Each course title refers to at most one course
courseTitleOf[c1] = ct, courseTitleOf[c2] = ct -> c1 = c2.
// If a student got a grade for a course
// then that student enrolled in that course
gradeOfStudentInCourse[s, c] = _ -> enrolledIn(s, c).
The first line of the LogiQL code declares Student as an entity type whose instances are referenced by student numbers that are coded as integers. The colon ":" in hasStudentNr(s:n) distinguishes hasStudentNr as a refmode predicate, so this predicate is injective (mandatory, 1:1). Similarly, the next two lines declare the entity types Course and Grade, along with their reference modes.
The fourth and fifth lines of code declare the typing constraints on the studentNameOf and courseTitleOf predicates, using the square bracket notation to declare that the predicates are functional (many to one). The next line declares the typing constraints on the enrolledIn predicate. The next statement declares the typing constraints on the ternary gradeOfStudentInCourse predicate, using the square bracket notation to indicate that it is a many-to-many-to-one relationship.
Comments are prepended by "//", and describe the constraint declared in the code immediately following the comment. An underscore "_" denotes the anonymous variable, is used for existential quantification and is read as "something". For example, the mandatory role constraint expressed in LogiQL as "Student(s) -> studentNameOf[s] = _." corresponds to the logical formula "∀s(Student s → ∃x x hasStudentName x)".
The subset constraint coded as "gradeOfStudentInCourse[s, c] = _ -> enrolledIn(s, c)." corresponds to the logical formula "∀s,c [∃g inCourseGotGrade(s, c, g) → s enrolledIn c]".
To enter the schema in the free, cloud-based REPL tool, use a supported browser such as Chrome, Firefox, or Internet Explorer to access the website https://repl.logicblox.com. Alternatively, you can access https://developer.logicblox.com/playground/, then click the "Open in new window" link to show a full screen for entering the code.
Schema code is entered in one or more blocks of one or more lines of code, using the addblock command to enter each block. After the "/>" prompt, type the letter "a" and click the addblock option that then appears. This causes the addblock command (followed by a space) to be added to the code window. Typing a single quote after the addblock command causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your block of code (see Figure 6).
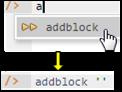
Figure 6. Invoking the addblock command in the REPL tool.
Now copy the schema code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. You are now notified that the block was successfully added, and a new prompt awaits your next command (see Figure 7). By default, the REPL tool also appends an automatically generated identifier for the code block. Alternatively, you can enter each line of code directly, using a separate addblock command for each line.
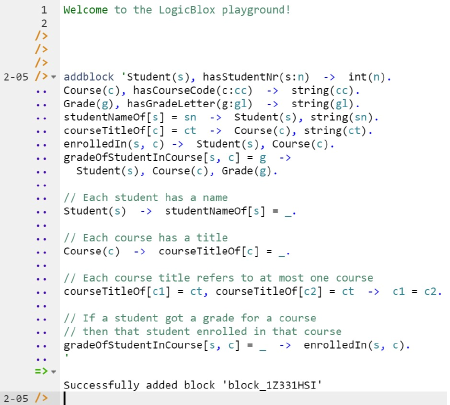
Figure 7. Adding a block of schema code.
The data in Table 1 may be entered in LogiQL using the following delta rules. A delta rule of the form +fact inserts that fact. Recall that plain, double quotes (i.e., ",") are needed here, not single quotes or smart double quotes. Hence it's best to use a basic text editor such as WordPad or NotePad to enter code that will later be copied into a LogiQL tool.
+Student(s), +hasStudentNr(s:101), +studentNameOf[s] = "Ann Jones".
+Student(s), +hasStudentNr(s:102), +studentNameOf[s] = "John Smith".
+Student(s), +hasStudentNr(s:103), +studentNameOf[s] = "John Smith".
+Course(c), +hasCourseCode(c:"CS100"), +courseTitleOf[c] = "Introduction to Computer Science".
+Course(c), +hasCourseCode(c:"CS102"), +courseTitleOf[c] =
"Programming Basics".
+Course(c), +hasCourseCode(c:"CS200"), +courseTitleOf[c] = "Operating Systems".
+Course(c), +hasCourseCode(c:"CS400"), +courseTitleOf[c] = "MetaInformatics".
+Grade(g), +hasGradeLetter(g:"A").
+Grade(g), +hasGradeLetter(g:"B").
+Student(s), +Course(c1), +Course(c2), +Course(c3), +Grade(g),
+hasStudentNr(s:101), +hasCourseCode(c1:"CS100"),
+hasCourseCode(c2:"CS102"), +hasCourseCode(c3:"CS200"),
+hasGradeLetter(g:"A"), +enrolledIn(s,c1), +enrolledIn(s,c2),
+enrolledIn(s,c3), +gradeOfStudentInCourse[s, c1] = g,
+gradeOfStudentInCourse[s, c2] = g.
+Student(s), +Course(c), +Grade(g), +hasStudentNr(s:102),
+hasCourseCode(c:"CS100"), +hasGradeLetter(g:"B"),
+enrolledIn(s,c), +gradeOfStudentInCourse[s, c] = g.
Note that, unlike early releases, LogiQL now requires the existence of entities and their reference schemes to be explicitly declared. For example, "+Student(s), +hasStudentNr(s:101)" is now needed to assert that there is a student who has student number 101, with the variable s referencing that student in other facts in the same statement. A future release will allow you to omit "+Student(p)" as the compiler will infer that from the typing constraint on a related fact assertion (e.g., +hasStudentNr(s:101)).
Delta rules to add or modify data are entered using the exec (for 'execute') command. To invoke the exec command in the REPL tool, type "e" and then select exec from the drop-down list. A space character is automatically appended. Typing a single quote after the exec command and space causes a pair of single quotes to be appended, with your cursor placed inside those quotes ready for your delta rules. Now copy the lines of data code provided above to the clipboard (e.g., using Ctrl+C), then paste it between the quotes (e.g., using Ctrl+V), and then press the Enter key. A new prompt awaits your next command (see Figure 8).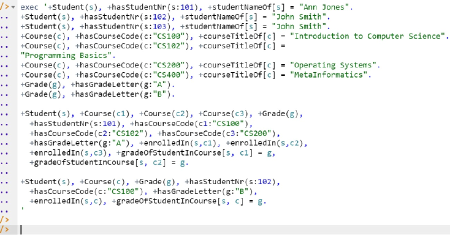
Figure 8. Adding the data below the program code.
Now that the data model (schema plus data) is stored, you can use the print command to inspect the contents of any predicate. For example, to list all the recorded students, type "p" then select print from the drop-down list, then type a space followed by "S", then select Student from the drop-down list and press Enter. Alternatively, type "print Student" yourself and press Enter. Figure 9 shows the result. By default, the REPL tool prepends a column listing automatically generated, internal identifiers for the returned entities. Similarly, you can use the print command to print the extension of the other predicates.
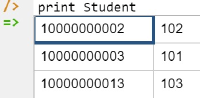
Figure 9. Using the print command to list the extension of a predicate.
As discussed in previous articles, to perform a query, you specify a derivation rule to compute the facts requested by the query. For example, the following query may be used to list the student number, name, and the grade in CS100 for those students who have a grade in that course. The rule's head _(n, sn, gl) uses an anonymous predicate to capture the result derived from the rule's body. The variables n, sn, and gl are head variables, so are implicitly universally quantified. The variables s, c, and g introduced in the rule body are implicitly existentially quantified.
_(n, sn, gl) <- hasStudentNr(s:n), studentNameOf[s] = sn, hasCourseCode(c:"CS100"),
hasGradeLetter(g:gl), gradeOfStudentInCourse[s, c] = g.
In LogiQL, queries are executed by appending their code in single quotes to the query command. To do this in the REPL tool, type "q", choose "query" from the drop-down list, type a single quote, then copy and paste the above LogiQL query code between the quotes and press Enter. The relevant query result is now displayed as shown in Figure 10.

Figure 10. A query to list the student number, name and grade in CS100 for those students with a grade in CS100.
Compound Subset Constraints involving Join Paths
Now suppose that in addition to recording each student's number and name we also record their title and gender, as indicated in Table 2. Here, genders are identified by gender codes ('M' for Male, and 'F' for Female). As an optional exercise, you may wish to model this report before reading on.
Table 2. Personal data about students.
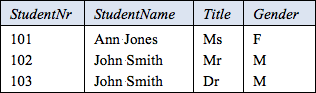
Figure 11 models Table 2 as a populated ORM schema. Notice the subset constraint. The role pair at the subset end consists of the first and last roles of the join path that traverses from Student to Gender via Title (where the conceptual join of the two roles hosted by Title requires the titles in the two predicates to match). The roles in the fact type Student is of Gender form the role pair at the superset end. The constraint requires, for each population of the database, that the set of (student, gender) role pairs projected from the join path must be a subset of the set of (student, gender) role pairs populating Student is of Gender.
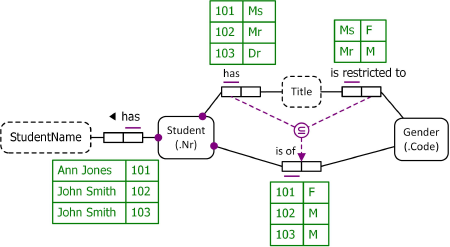
Figure 11. Populated ORM model for Table 2.
A subset constraint involving a join path is called a join-subset constraint. The NORMA tool[4] verbalizes the join-subset constraint in Figure 11 as follows:
If some Student has some Title
that is restricted to some Gender
then that Student is of that Gender.
Some titles like "Mr" and "Sir" are restricted to males, some titles like "Ms", "Mrs", and "Lady" are restricted to females, while some titles like "Dr" and "Prof" are allowed for both genders. The join-subset constraint prevents errors such as asserting that student 102 is male and has the title "Ms". For completeness, a value constraint should be added to restrict gender codes to the set {'M', 'F'}, but discussion of value constraints is delayed to a later article.
In Figure 11 the object type Title is not declared independent, so its population is understood to be the union of its role populations (for the data shown, this is the set {'Ms', 'Mr', 'Dr'}). Suppose that we now wish to record each title of interest, along with its gender restriction (if any), whether or not any student has that title. In this case, we need to declare Title as independent, to allow some of its instances to exist independently of playing any roles. The ORM schema for this situation, along with a sample population, is shown in Figure 12. To automatically generate better column names for relational mapping, the role name "restrictedGender" has been added to Gender's role in the Title is restricted to Gender fact type.
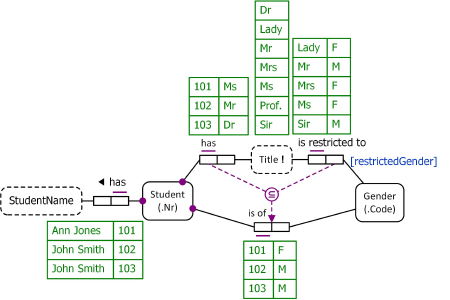
Figure 12. Populated ORM model for Table 2, that also allows titles to be listed independently of playing roles.
Figure 13 shows the relational schema diagram generated by NORMA from the ORM schema shown in Figure 12. The restrictedGender attribute is displayed in plain (not bold) type, so is nullable.
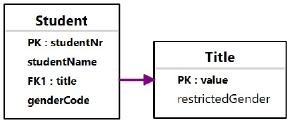
Figure 13. Relational schema diagram obtained by using NORMA to map the ORM schema in Figure 12.
Though not captured graphically in the relational schema diagram, the join subset constraint may be coded in SQL. For example, if the SQL dialect supports assertions, the following SQL code may be used.
create assertion title_gender_constraint
check ( not exists
( select *
from Student join Title
on Student.title = Title.value
where genderCode <> restrictedGender ) )
Figure 14 shows simple attempts to schematize Table 2 in the graphical notation of Barker ER and UML. Title and gender are modeled as attributes, and relationships are not allowed between attributes, so neither of these attempts can capture facts about title gender restrictions or the join subset constraint under discussion.
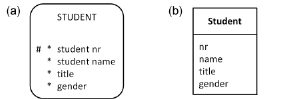
Figure 14. Simple attempts to model Table 2 in (a) Barker ER and (b) UML notation.
Although unusual for attribute-based notations such as ER and UML, we could instead treat Title as an entity type or class as shown in Figure 15, enabling title gender restrictions to be captured. While the Barker ER notation cannot depict the join subset constraint, in UML we can at least add a comment with the subset constraint specified textually in OCL code,[18] as shown in Figure 15(b). However, for validation with non-technical domain experts, the OCL code is less suitable than NORMA's verbalization of the subset constraint shown earlier.
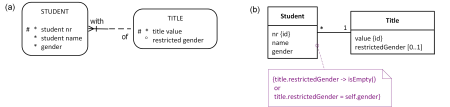
Figure 15. Further attempts to model Table 2 in (a) Barker ER and (b) UML notation.
The schema for Table 2 may be coded in LogiQL as follows. The first two lines declare the reference modes for Student and Gender. The next four lines declare types and functionality of the four fact types. The next line declares the mandatory role constraints on those fact types. A comment explaining the join subset constraint is then provided, followed by the constraint code itself. This corresponds to the logical formula ∀s,g [∃t(s hasTitle t & t isRestrictedTo g) → s hasGender g].
Student(s), hasStudentNr(s:n) -> int(n).
Gender(g), hasGenderCode(g:gc) -> string(gc).
studentNameOf[s] = sn -> Student(s), string(sn).
titleOf[s] = t -> Student(s), string(t).
genderOf[s] = g -> Student(s), Gender(g).
requiredGenderFor[t] = g -> string(t), Gender(g).
Student(s) -> studentNameOf[s] = _, titleOf[s] = _, genderOf[s] = _.
/* If student s has a title t that is restricted to gender g
then student s must be of gender g */
titleOf[s] = t, requiredGenderFor[t] = g -> genderOf[s] = g.
Use the addblock command to add this code to the workspace in the usual way. The sample data (including gender restrictions for the titles in Table 2) may be coded in LogiQL using the following delta rules.
+Student(s), +hasStudentNr(s:101), +studentNameOf[s] = "Ann Jones", +titleOf[s] = "Ms",
+Gender(g), +hasGenderCode(g:"F"), +genderOf[s] = g.+Student(s), +hasStudentNr(s:102), +studentNameOf[s] = "John Smith", +titleOf[s] = "Mr",
+Gender(g), +hasGenderCode(g:"M"), +genderOf[s] = g.+Student(s), +hasStudentNr(s:103), +studentNameOf[s] = "John Smith", +titleOf[s] = "Dr",
+Gender(g), +hasGenderCode(g:"M"), +genderOf[s] = g.+Gender(g), +hasGenderCode(g:"F"), +requiredGenderFor["Ms"] = g.
+Gender(g), +hasGenderCode(g:"M"), +requiredGenderFor["Mr"] = g.
Now use the exec command in the usual way to enter the delta rules. The following query may now be used to list the student number, name and title of the male students.
_(n, sn, t) <- hasStudentNr(s:n), studentNameOf[s] = sn, titleOf[s] = t, genderOf[s] = g,
hasGenderCode(g:"M").
Entering this query causes the relevant result to be displayed as shown in Figure 16.

Figure 16. Querying the workspace to list personal details of male students.
Conclusion
The current article discussed how to declare compound subset constraints, including case involving join paths. As discussed in the next article, exclusion and equality constraints may also be declared between compound role sequences, so long as these role sequences are compatible. Future articles in this series will examine how LogiQL can be used to specify business constraints and rules of a more advanced nature. The core reference manual for LogiQL is accessible at https://developer.logicblox.com/content/docs4/core-reference/. An introductory tutorial for LogiQL and the REPL tool is available at https://developer.logicblox.com/content/docs4/tutorial/repl/section/split.html. Further coverage of LogiQL may be found in [14].
References
[1] S. Abiteboul, R. Hull, & V. Vianu, Foundations of Databases, Addison-Wesley, Reading, MA (1995). ![]()
[2] M. Aref, B. Cate, T. Green, B. Kimefeld, D. Olteanu, E. Pasalic, T. Veldhuizen, & G. Washburn, "Design and Implementation of the LogicBlox System," Proc. 2015 ACM SIGMOD International Conference on Management of Data, ACM, New York (2015). http://dx.doi.org/10.1145/2723372.2742796 ![]()
[3] R. Barker, CASE*Method: Entity Relationship Modelling, Addison-Wesley: Wokingham, England (1990). ![]()
[4] M. Curland & T. Halpin, "The NORMA Software Tool for ORM 2," P. Soffer & E. Proper (Eds.): CAiSE Forum 2010, LNBIP 72, Springer-Verlag Berlin Heidelberg (2010), pp. 190-204. ![]()
[5] T.A. Halpin, "Logical Data Modeling (Part
1)," Business Rules Journal, Vol. 15, No. 5 (May 2014), URL: http://www.BRCommunity.com/a2014/b760.html ![]()
[6] T.A. Halpin, "Logical Data Modeling (Part
2)," Business Rules Journal, Vol. 15, No. 10 (Oct. 2014), URL: http://www.BRCommunity.com/a2014/b780.html ![]()
[7] T.A. Halpin, "Logical Data Modeling (Part
3)," Business Rules Journal, Vol. 16, No. 1 (Jan. 2015), URL: http://www.BRCommunity.com/a2015/b795.html ![]()
[8] T.A. Halpin, "Logical Data Modeling (Part
4)," Business Rules Journal, Vol. 16, No. 7 (July 2015), URL: http://www.BRCommunity.com/a2015/b820.html ![]()
[9] T.A. Halpin, "Logical Data Modeling (Part
5)," Business Rules Journal, Vol. 16, No. 10 (Oct. 2015), URL: http://www.BRCommunity.com/a2015/b832.html ![]()
[10] T.A. Halpin, "Logical Data Modeling (Part
6)," Business Rules Journal, Vol. 17, No. 3 (Mar. 2016), URL: http://www.BRCommunity.com/a2016/b852.html ![]()
[11] T.A. Halpin, Object-Role Modeling Fundamentals, Technics Publications: New Jersey (2015). ![]()
[12] T.A. Halpin, Object-Role Modeling Workbook, Technics Publications: New Jersey (2016). ![]()
[13] T.A. Halpin & T. Morgan, Information Modeling and Relational Databases, 2nd edition, Morgan Kaufmann: San Francisco (2008). ![]()
[14] T.A. Halpin & S. Rugaber, LogiQL: A Query language for Smart Databases, CRC Press: Boca Raton (2014); http://www.crcpress.com/product/isbn/9781482244939# ![]()
[15] T.A. Halpin & J. Wijbenga, "FORML 2," Enterprise, Business-Process and Information Systems Modeling, eds. I. Bider et al., LNBIP 50, Springer-Verlag, Berlin Heidelberg (2010), pp. 247–260.
[16] S. Huang, T. Green, & B. Loo, "Datalog and emerging applications: an interactive tutorial," Proc. 2011 ACM SIGMOD International Conference on Management of Data, ACM, New York (2011). At: http://dl.acm.org/citation.cfm?id=1989456 ![]()
[17] Object Management Group, OMG Unified Modeling Language Specification (OMG UML), version 2.5 RTF Beta 2, Object Management Group (2013). Available online at: http://www.omg.org/spec/UML/2.5/ ![]()
[18] Object Management Group, OMG Object Constraint Language (OCL), version 2.3.1, Object Management Group (2012). Retrieved from http://www.omg.org/spec/OCL/2.3.1/ ![]()
# # #
About our Contributor:
Online Interactive Training Series
In response to a great many requests, Business Rule Solutions now offers at-a-distance learning options. No travel, no backlogs, no hassles. Same great instructors, but with schedules, content and pricing designed to meet the special needs of busy professionals.












How to Define Business Terms in Plain English: A Primer
How to Use DecisionSpeak™ and Question Charts (Q-Charts™)
Decision Tables - A Primer: How to Use TableSpeak™
Tabulation of Lists in RuleSpeak®: A Primer - Using "The Following" Clause
Business Agility Manifesto
Business Rules Manifesto
Business Motivation Model
Decision Vocabulary
[Download]
[Download]
Semantics of Business Vocabulary and Business Rules